Teaching-Inspired Integrated Prompting Framework: A Novel Approach for Enhancing Reasoning in Large Language Models

Large Language Models (LLMs) exhibit impressive performance across various domains but still struggle with arithmetic reasoning tasks. Recent work shows the effectiveness of prompt design methods in enhancing reasoning capabilities. However, these approaches overlook crucial requirements for prior knowledge of specific concepts, theorems, and tricks to tackle most arithmetic reasoning problems successfully. To address this issue, we propose a novel and effective Teaching-Inspired Integrated Framework, which emulates the instructional process of a teacher guiding students. This method equips LLMs with essential concepts, relevant theorems, and similar problems with analogous solution approaches, facilitating the enhancement of reasoning abilities. Additionally, we introduce two new Chinese datasets, MathMC and MathToF, both with detailed explanations and answers. Experiments are conducted on nine benchmarks which demonstrates that our approach improves the reasoning accuracy of LLMs. With GPT-4 and our framework, we achieve new state-of-the-art performance on four math benchmarks (AddSub, SVAMP, Math23K and AQuA) with accuracies of 98.2% (+3.3%), 93.9% (+0.2%), 94.3% (+7.2%) and 81.1% (+1.2%). Our data and code are available at https://github.com/SallyTan13/Teaching-Inspired-Prompting.

From Large to Tiny: Distilling and Refining Mathematical Expertise for Math Word Problems with Weakly Supervision

Addressing the challenge of high annotation costs in solving Math Word Problems (MWPs) through full supervision with intermediate equations, recent works have proposed weakly supervised task settings that rely solely on the final answer as a supervised signal. Existing leading approaches typically employ various search techniques to infer intermediate equations, but cannot ensure their semantic consistency with natural language descriptions. The rise of Large Language Models (LLMs) like ChatGPT has opened up new possibilities for addressing MWPs directly. However, the computational demands of LLMs make them less than ideal for use in settings where resources are tight. In light of these challenges, we introduce an innovative two-stage framework that adeptly transfers mathematical Expertise from large to tiny language models. In \emph{Distillation Stage}, we propose a series of extraction processes that satisfy the properties of MWPs to distill mathematical knowledge from LLMs to construct problem-equation pairs required for supervised training. In \emph{Refinement Stage}, Due to Knowledge distilling method cannot guarantee the full utilization of all data, we further utilize the unsuccessfully searched data effectively by Knowledge Refine method. Finally, We train a small model using distilled data generated through two-stage methods. As our method fully leverages the semantic understanding capabilities during the searching 'problem-equation' pair, it demonstrates significantly improved performance on the Math23K and Weak12K datasets compared to existing small model methods, while maintaining a much lower computational cost than ChatGPT.

Learning by Analogy: Diverse Questions Generation in Math Word Problem

Solving math word problem (MWP) with AI techniques has recently made great progress with the success of deep neural networks (DNN), but it is far from being solved. We argue that the ability of learning by analogy is essential for an MWP solver to better understand same problems which may typically be formulated in diverse ways. However most existing works exploit the shortcut learning to train MWP solvers simply based on samples with a single question. In lack of diverse questions, these methods merely learn shallow heuristics. In this paper, we make a first attempt to solve MWPs by generating diverse yet consistent questions/equations. Given a typical MWP including the scenario description, question, and equation (i.e., answer), we first generate multiple consistent equations via a group of heuristic rules. We then feed them to a question generator together with the scenario to obtain the corresponding diverse questions, forming a new MWP with a variety of questions and equations. Finally we engage a data filter to remove those unreasonable MWPs, keeping the high-quality augmented ones. To evaluate the ability of learning by analogy for an MWP solver, we generate a new MWP dataset (called DiverseMath23K) with diverse questions by extending the current benchmark Math23K. Extensive experimental results demonstrate that our proposed method can generate high-quality diverse questions with corresponding equations, further leading to performance improvement on Diverse-Math23K. The code and dataset is available at: https://github.com/zhouzihao501/DiverseMWP

Non-Autoregressive Math Word Problem Solver with Unified Tree Structure

Existing MWP solvers employ sequence or binary tree to present the solution expression and decode it from given problem description. However, such structures fail to handle the identical variants derived via mathematical manipulation, e.g., $(a_1+a_2)*a_3$ and $a_1*a_3+a_2*a_3$ are for the same problem but formulating different expression sequences and trees, which would raise two issues in MWP solving: 1) different output solutions for the same input problem, making the model hard to learn the mapping function between input and output spaces, and 2) difficulty of evaluating solution expression that indicates wrong between the above examples. To address these issues, we first introduce a unified tree structure to present expression, where the elements are permutable and identical for all the expression variants. We then propose a novel non-autoregressive solver, dubbed MWP-NAS, to parse the problem and reason the solution expression based on the unified tree. For the second issue, to handle the variants in evaluation, we propose to match the unified tree and design a path-based metric to evaluate the partial accuracy of expression. Extensive experiments have been conducted on Math23K and MAWPS, and the results demonstrate the effectiveness of the proposed MWP-NAS. The codes and checkpoints are available at: https://github.com/mengqunhan/MWP-NAS

Analogical Math Word Problems Solving with Enhanced Problem-Solution Association

Math word problem (MWP) solving is an important task in question answering which requires human-like reasoning ability. Analogical reasoning has long been used in mathematical education, as it enables students to apply common relational structures of mathematical situations to solve new problems. In this paper, we propose to build a novel MWP solver by leveraging analogical MWPs, which advance the solver's generalization ability across different kinds of MWPs. The key idea, named analogy identification, is to associate the analogical MWP pairs in a latent space, i.e., encoding an MWP close to another analogical MWP, while moving away from the non-analogical ones. Moreover, a solution discriminator is integrated into the MWP solver to enhance the association between the representations of MWPs and their true solutions. The evaluation results verify that our proposed analogical learning strategy promotes the performance of MWP-BERT on Math23k over the state-of-the-art model Generate2Rank, with 5 times fewer parameters in the encoder. We also find that our model has a stronger generalization ability in solving difficult MWPs due to the analogical learning from easy MWPs.

Generalizing Math Word Problem Solvers via Solution Diversification

Current math word problem (MWP) solvers are usually Seq2Seq models trained by the (one-problem; one-solution) pairs, each of which is made of a problem description and a solution showing reasoning flow to get the correct answer. However, one MWP problem naturally has multiple solution equations. The training of an MWP solver with (one-problem; one-solution) pairs excludes other correct solutions, and thus limits the generalizability of the MWP solver. One feasible solution to this limitation is to augment multiple solutions to a given problem. However, it is difficult to collect diverse and accurate augment solutions through human efforts. In this paper, we design a new training framework for an MWP solver by introducing a solution buffer and a solution discriminator. The buffer includes solutions generated by an MWP solver to encourage the training data diversity. The discriminator controls the quality of buffered solutions to participate in training. Our framework is flexibly applicable to a wide setting of fully, semi-weakly and weakly supervised training for all Seq2Seq MWP solvers. We conduct extensive experiments on a benchmark dataset Math23k and a new dataset named Weak12k, and show that our framework improves the performance of various MWP solvers under different settings by generating correct and diverse solutions.

Seeking Diverse Reasoning Logic: Controlled Equation Expression Generation for Solving Math Word Problems

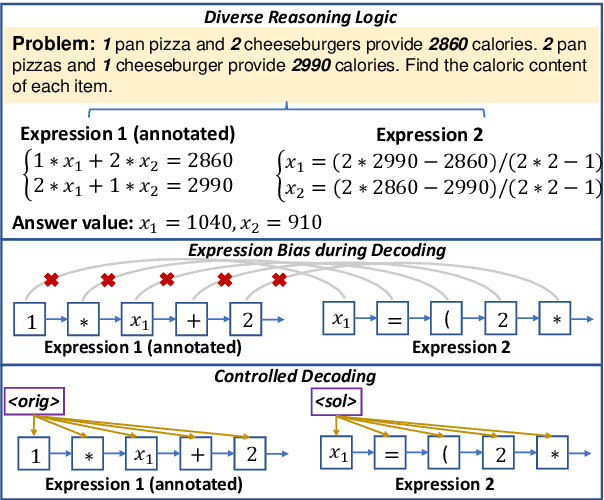
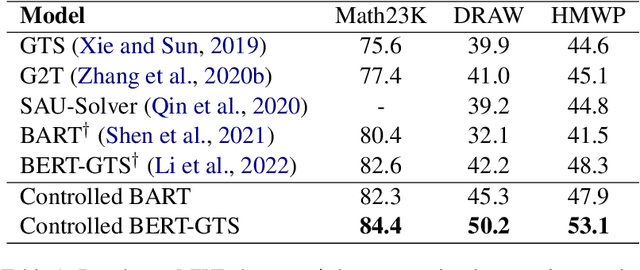
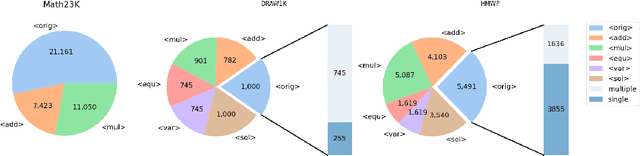
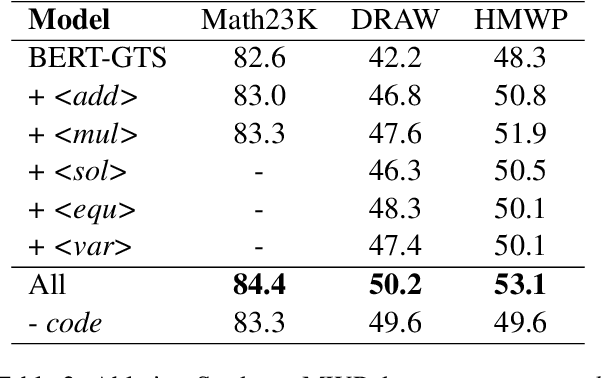
To solve Math Word Problems, human students leverage diverse reasoning logic that reaches different possible equation solutions. However, the mainstream sequence-to-sequence approach of automatic solvers aims to decode a fixed solution equation supervised by human annotation. In this paper, we propose a controlled equation generation solver by leveraging a set of control codes to guide the model to consider certain reasoning logic and decode the corresponding equations expressions transformed from the human reference. The empirical results suggest that our method universally improves the performance on single-unknown (Math23K) and multiple-unknown (DRAW1K, HMWP) benchmarks, with substantial improvements up to 13.2% accuracy on the challenging multiple-unknown datasets.

Tackling Math Word Problems with Fine-to-Coarse Abstracting and Reasoning

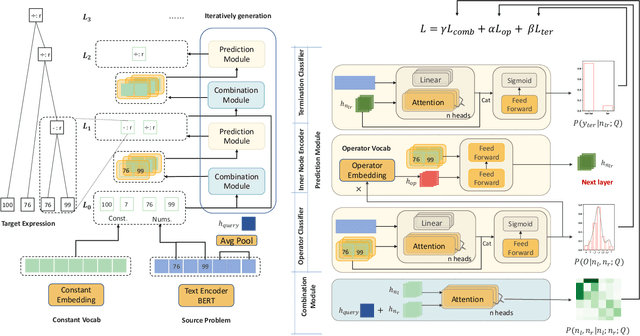
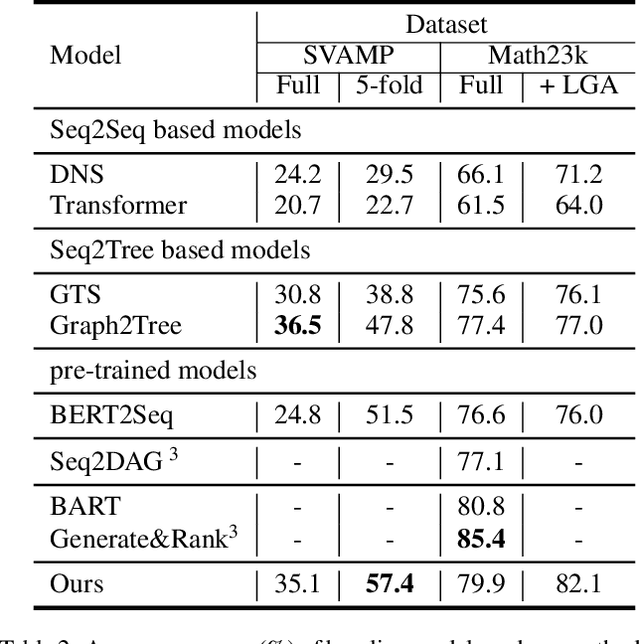
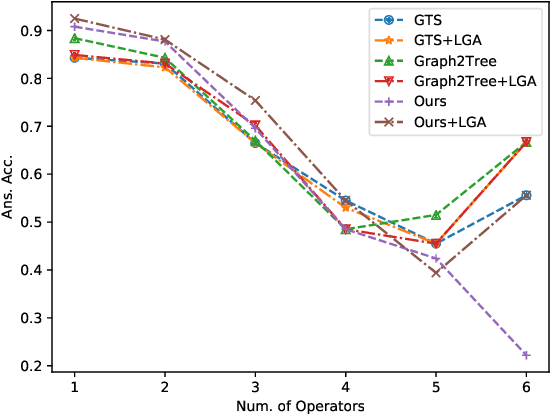
Math Word Problems (MWP) is an important task that requires the ability of understanding and reasoning over mathematical text. Existing approaches mostly formalize it as a generation task by adopting Seq2Seq or Seq2Tree models to encode an input math problem in natural language as a global representation and generate the output mathematical expression. Such approaches only learn shallow heuristics and fail to capture fine-grained variations in inputs. In this paper, we propose to model a math word problem in a fine-to-coarse manner to capture both the local fine-grained information and the global logical structure of it. Instead of generating a complete equation sequence or expression tree from the global features, we iteratively combine low-level operands to predict a higher-level operator, abstracting the problem and reasoning about the solving operators from bottom to up. Our model is naturally more sensitive to local variations and can better generalize to unseen problem types. Extensive evaluations on Math23k and SVAMP datasets demonstrate the accuracy and robustness of our method.

Seeking Patterns, Not just Memorizing Procedures: Contrastive Learning for Solving Math Word Problems

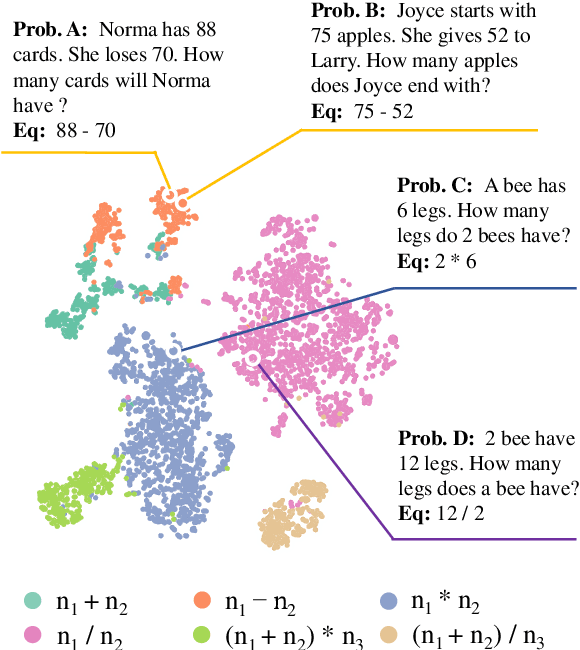
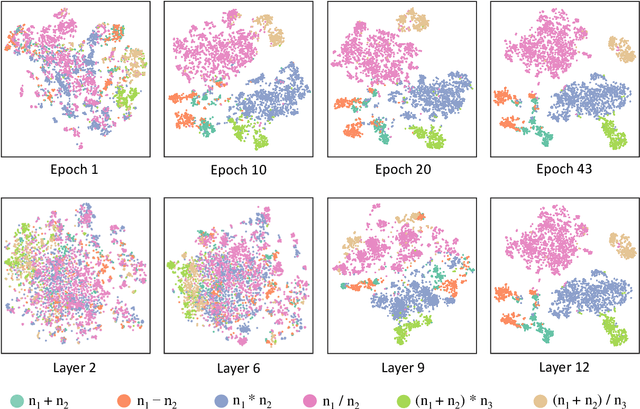
Math Word Problem (MWP) solving needs to discover the quantitative relationships over natural language narratives. Recent work shows that existing models memorize procedures from context and rely on shallow heuristics to solve MWPs. In this paper, we look at this issue and argue that the cause is a lack of overall understanding of MWP patterns. We first investigate how a neural network understands patterns only from semantics, and observe that, if the prototype equations are the same, most problems get closer representations and those representations apart from them or close to other prototypes tend to produce wrong solutions. Inspired by it, we propose a contrastive learning approach, where the neural network perceives the divergence of patterns. We collect contrastive examples by converting the prototype equation into a tree and seeking similar tree structures. The solving model is trained with an auxiliary objective on the collected examples, resulting in the representations of problems with similar prototypes being pulled closer. We conduct experiments on the Chinese dataset Math23k and the English dataset MathQA. Our method greatly improves the performance in monolingual and multilingual settings.

Generate & Rank: A Multi-task Framework for Math Word Problems

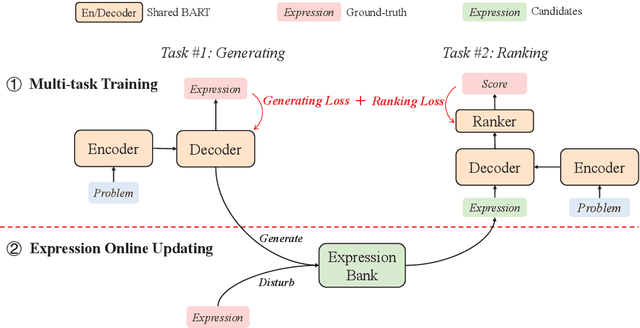
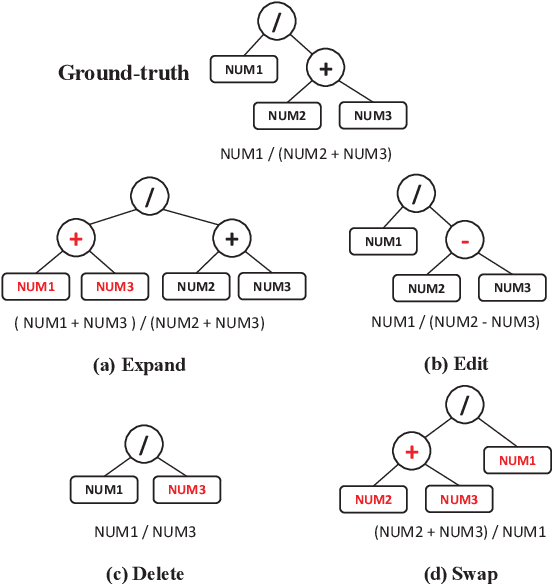
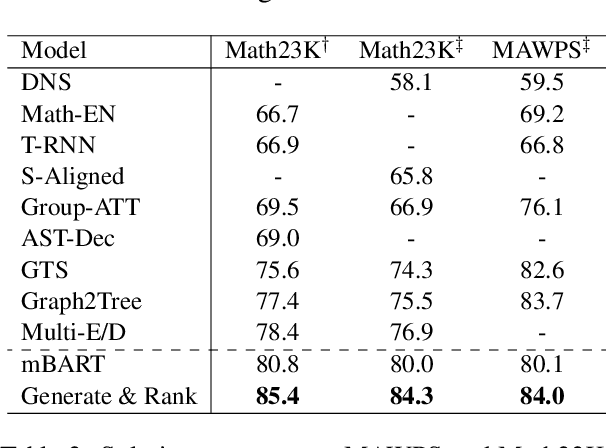
Math word problem (MWP) is a challenging and critical task in natural language processing. Many recent studies formalize MWP as a generation task and have adopted sequence-to-sequence models to transform problem descriptions to mathematical expressions. However, mathematical expressions are prone to minor mistakes while the generation objective does not explicitly handle such mistakes. To address this limitation, we devise a new ranking task for MWP and propose Generate & Rank, a multi-task framework based on a generative pre-trained language model. By joint training with generation and ranking, the model learns from its own mistakes and is able to distinguish between correct and incorrect expressions. Meanwhile, we perform tree-based disturbance specially designed for MWP and an online update to boost the ranker. We demonstrate the effectiveness of our proposed method on the benchmark and the results show that our method consistently outperforms baselines in all datasets. Particularly, in the classical Math23k, our method is 7% (78.4% $\rightarrow$ 85.4%) higher than the state-of-the-art.