Text-to-SQL Domain Adaptation via Human-LLM Collaborative Data Annotation

Text-to-SQL models, which parse natural language (NL) questions to executable SQL queries, are increasingly adopted in real-world applications. However, deploying such models in the real world often requires adapting them to the highly specialized database schemas used in specific applications. We find that existing text-to-SQL models experience significant performance drops when applied to new schemas, primarily due to the lack of domain-specific data for fine-tuning. This data scarcity also limits the ability to effectively evaluate model performance in new domains. Continuously obtaining high-quality text-to-SQL data for evolving schemas is prohibitively expensive in real-world scenarios. To bridge this gap, we propose SQLsynth, a human-in-the-loop text-to-SQL data annotation system. SQLsynth streamlines the creation of high-quality text-to-SQL datasets through human-LLM collaboration in a structured workflow. A within-subjects user study comparing SQLsynth with manual annotation and ChatGPT shows that SQLsynth significantly accelerates text-to-SQL data annotation, reduces cognitive load, and produces datasets that are more accurate, natural, and diverse. Our code is available at https://github.com/adobe/nl_sql_analyzer.

From Documents to Dialogue: Building KG-RAG Enhanced AI Assistants

The Adobe Experience Platform AI Assistant is a conversational tool that enables organizations to interact seamlessly with proprietary enterprise data through a chatbot. However, due to access restrictions, Large Language Models (LLMs) cannot retrieve these internal documents, limiting their ability to generate accurate zero-shot responses. To overcome this limitation, we use a Retrieval-Augmented Generation (RAG) framework powered by a Knowledge Graph (KG) to retrieve relevant information from external knowledge sources, enabling LLMs to answer questions over private or previously unseen document collections. In this paper, we propose a novel approach for building a high-quality, low-noise KG. We apply several techniques, including incremental entity resolution using seed concepts, similarity-based filtering to deduplicate entries, assigning confidence scores to entity-relation pairs to filter for high-confidence pairs, and linking facts to source documents for provenance. Our KG-RAG system retrieves relevant tuples, which are added to the user prompts context before being sent to the LLM generating the response. Our evaluation demonstrates that this approach significantly enhances response relevance, reducing irrelevant answers by over 50% and increasing fully relevant answers by 88% compared to the existing production system.

CodeLutra: Boosting LLM Code Generation via Preference-Guided Refinement

Large Language Models (LLMs) have significantly advanced code generation but often require substantial resources and tend to over-generalize, limiting their efficiency for specific tasks. Fine-tuning smaller, open-source LLMs presents a viable alternative; however, it typically lags behind cutting-edge models due to supervised fine-tuning's reliance solely on correct code examples, which restricts the model's ability to learn from its own mistakes and adapt to diverse programming challenges. To bridge this gap, we introduce CodeLutra, a novel framework that enhances low-performing LLMs by leveraging both successful and failed code generation attempts. Unlike conventional fine-tuning, CodeLutra employs an iterative preference learning mechanism to compare correct and incorrect solutions as well as maximize the likelihood of correct codes. Through continuous iterative refinement, CodeLutra enables smaller LLMs to match or surpass GPT-4's performance in various code generation tasks without relying on vast external datasets or larger auxiliary models. On a challenging data analysis task, using just 500 samples improved Llama-3-8B's accuracy from 28.2% to 48.6%, approaching GPT-4's performance. These results highlight CodeLutra's potential to close the gap between open-source and closed-source models, making it a promising approach in the field of code generation.

Hallucination Diversity-Aware Active Learning for Text Summarization

Large Language Models (LLMs) have shown propensity to generate hallucinated outputs, i.e., texts that are factually incorrect or unsupported. Existing methods for alleviating hallucinations typically require costly human annotations to identify and correct hallucinations in LLM outputs. Moreover, most of these methods focus on a specific type of hallucination, e.g., entity or token errors, which limits their effectiveness in addressing various types of hallucinations exhibited in LLM outputs. To our best knowledge, in this paper we propose the first active learning framework to alleviate LLM hallucinations, reducing costly human annotations of hallucination needed. By measuring fine-grained hallucinations from errors in semantic frame, discourse and content verifiability in text summarization, we propose HAllucination Diversity-Aware Sampling (HADAS) to select diverse hallucinations for annotations in active learning for LLM finetuning. Extensive experiments on three datasets and different backbone models demonstrate advantages of our method in effectively and efficiently mitigating LLM hallucinations.

Optimal Sketching Bounds for Sparse Linear Regression

We study oblivious sketching for $k$-sparse linear regression under various loss functions such as an $\ell_p$ norm, or from a broad class of hinge-like loss functions, which includes the logistic and ReLU losses. We show that for sparse $\ell_2$ norm regression, there is a distribution over oblivious sketches with $\Theta(k\log(d/k)/\varepsilon^2)$ rows, which is tight up to a constant factor. This extends to $\ell_p$ loss with an additional additive $O(k\log(k/\varepsilon)/\varepsilon^2)$ term in the upper bound. This establishes a surprising separation from the related sparse recovery problem, which is an important special case of sparse regression. For this problem, under the $\ell_2$ norm, we observe an upper bound of $O(k \log (d)/\varepsilon + k\log(k/\varepsilon)/\varepsilon^2)$ rows, showing that sparse recovery is strictly easier to sketch than sparse regression. For sparse regression under hinge-like loss functions including sparse logistic and sparse ReLU regression, we give the first known sketching bounds that achieve $o(d)$ rows showing that $O(\mu^2 k\log(\mu n d/\varepsilon)/\varepsilon^2)$ rows suffice, where $\mu$ is a natural complexity parameter needed to obtain relative error bounds for these loss functions. We again show that this dimension is tight, up to lower order terms and the dependence on $\mu$. Finally, we show that similar sketching bounds can be achieved for LASSO regression, a popular convex relaxation of sparse regression, where one aims to minimize $\|Ax-b\|_2^2+\lambda\|x\|_1$ over $x\in\mathbb{R}^d$. We show that sketching dimension $O(\log(d)/(\lambda \varepsilon)^2)$ suffices and that the dependence on $d$ and $\lambda$ is tight.

Sample Constrained Treatment Effect Estimation

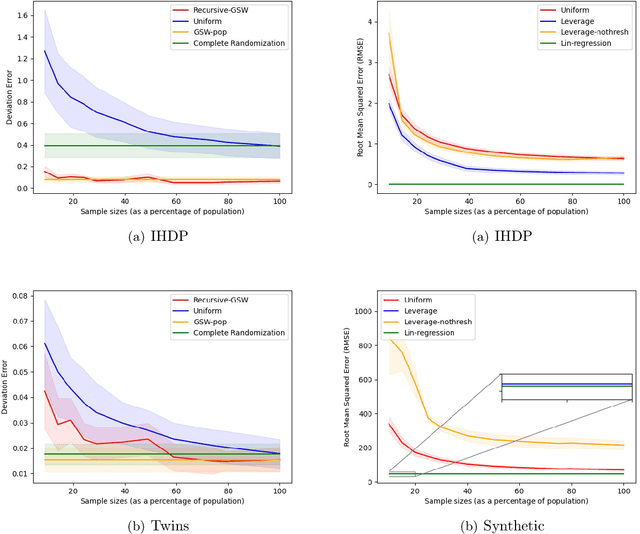
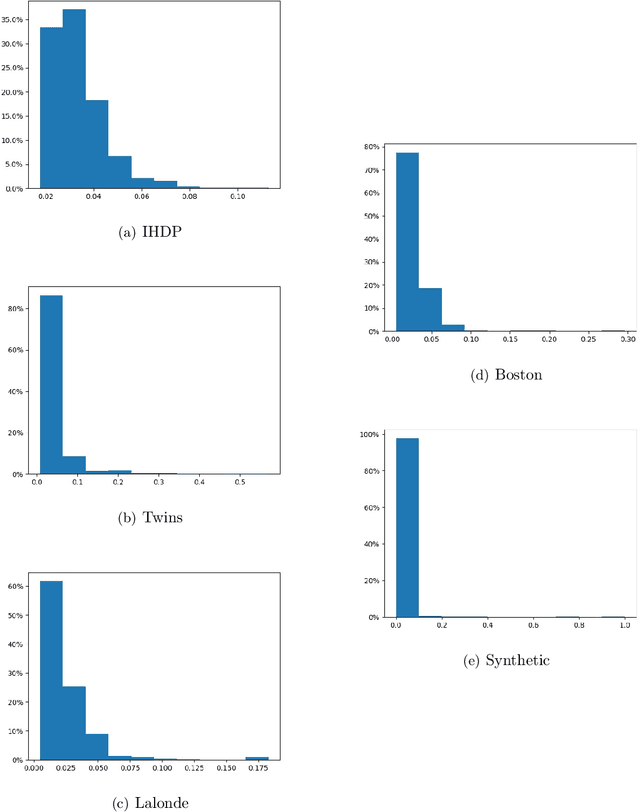
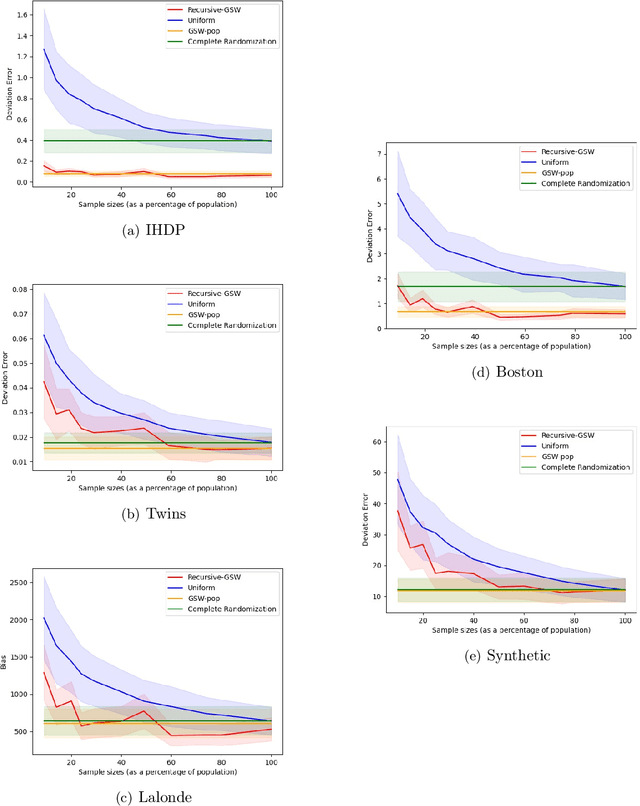
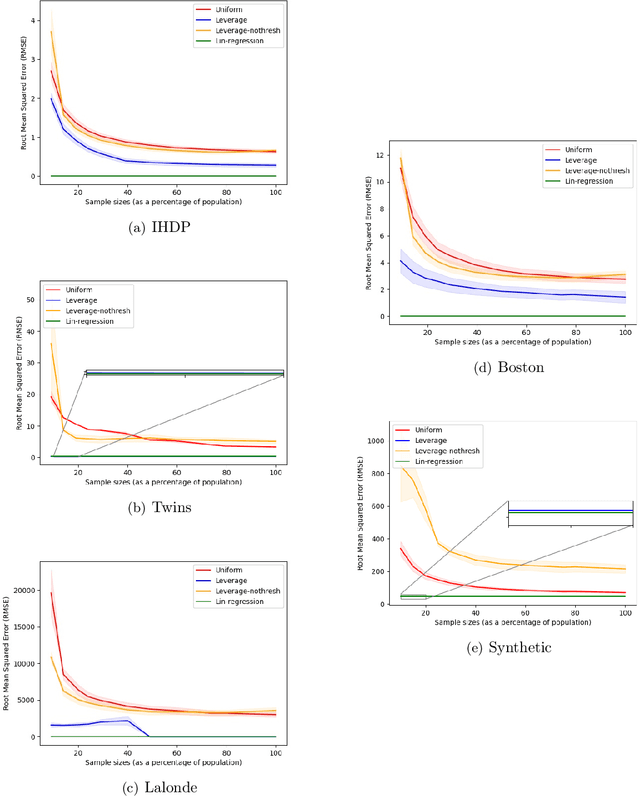
Treatment effect estimation is a fundamental problem in causal inference. We focus on designing efficient randomized controlled trials, to accurately estimate the effect of some treatment on a population of $n$ individuals. In particular, we study sample-constrained treatment effect estimation, where we must select a subset of $s \ll n$ individuals from the population to experiment on. This subset must be further partitioned into treatment and control groups. Algorithms for partitioning the entire population into treatment and control groups, or for choosing a single representative subset, have been well-studied. The key challenge in our setting is jointly choosing a representative subset and a partition for that set. We focus on both individual and average treatment effect estimation, under a linear effects model. We give provably efficient experimental designs and corresponding estimators, by identifying connections to discrepancy minimization and leverage-score-based sampling used in randomized numerical linear algebra. Our theoretical results obtain a smooth transition to known guarantees when $s$ equals the population size. We also empirically demonstrate the performance of our algorithms.

Electra: Conditional Generative Model based Predicate-Aware Query Approximation

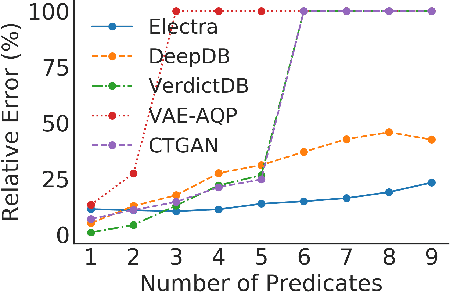
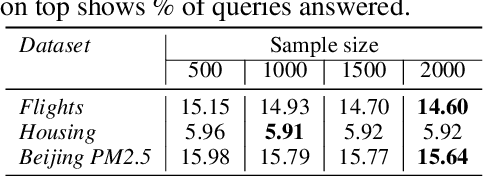
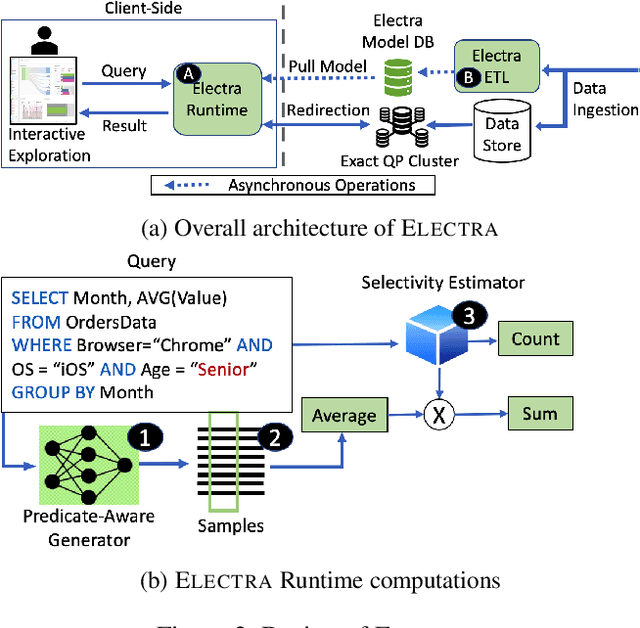
The goal of Approximate Query Processing (AQP) is to provide very fast but "accurate enough" results for costly aggregate queries thereby improving user experience in interactive exploration of large datasets. Recently proposed Machine-Learning based AQP techniques can provide very low latency as query execution only involves model inference as compared to traditional query processing on database clusters. However, with increase in the number of filtering predicates(WHERE clauses), the approximation error significantly increases for these methods. Analysts often use queries with a large number of predicates for insights discovery. Thus, maintaining low approximation error is important to prevent analysts from drawing misleading conclusions. In this paper, we propose ELECTRA, a predicate-aware AQP system that can answer analytics-style queries with a large number of predicates with much smaller approximation errors. ELECTRA uses a conditional generative model that learns the conditional distribution of the data and at runtime generates a small (~1000 rows) but representative sample, on which the query is executed to compute the approximate result. Our evaluations with four different baselines on three real-world datasets show that ELECTRA provides lower AQP error for large number of predicates compared to baselines.

Online MAP Inference and Learning for Nonsymmetric Determinantal Point Processes

In this paper, we introduce the online and streaming MAP inference and learning problems for Non-symmetric Determinantal Point Processes (NDPPs) where data points arrive in an arbitrary order and the algorithms are constrained to use a single-pass over the data as well as sub-linear memory. The online setting has an additional requirement of maintaining a valid solution at any point in time. For solving these new problems, we propose algorithms with theoretical guarantees, evaluate them on several real-world datasets, and show that they give comparable performance to state-of-the-art offline algorithms that store the entire data in memory and take multiple passes over it.

An Interpretable Graph Generative Model with Heterophily

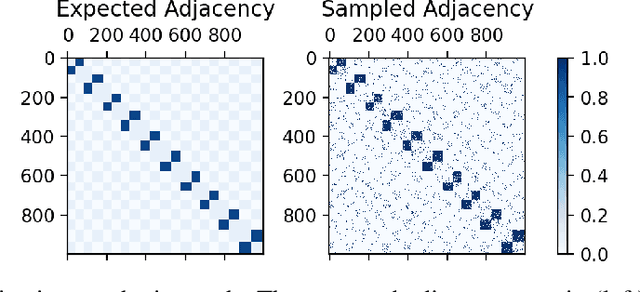
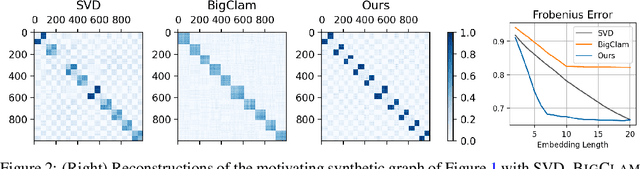
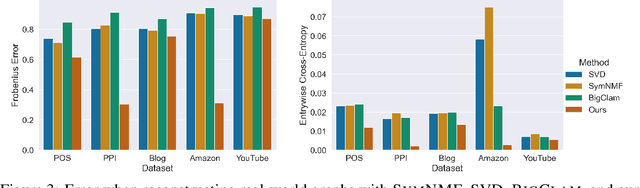
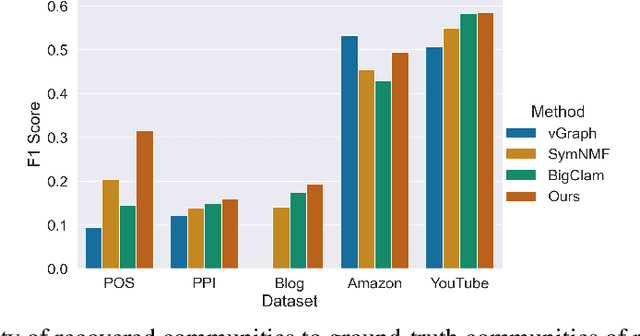
Many models for graphs fall under the framework of edge-independent dot product models. These models output the probabilities of edges existing between all pairs of nodes, and the probability of a link between two nodes increases with the dot product of vectors associated with the nodes. Recent work has shown that these models are unable to capture key structures in real-world graphs, particularly heterophilous structures, wherein links occur between dissimilar nodes. We propose the first edge-independent graph generative model that is a) expressive enough to capture heterophily, b) produces nonnegative embeddings, which allow link predictions to be interpreted in terms of communities, and c) optimizes effectively on real-world graphs with gradient descent on a cross-entropy loss. Our theoretical results demonstrate the expressiveness of our model in its ability to exactly reconstruct a graph using a number of clusters that is linear in the maximum degree, along with its ability to capture both heterophily and homophily in the data. Further, our experiments demonstrate the effectiveness of our model for a variety of important application tasks such as multi-label clustering and link prediction.

Coresets for Classification -- Simplified and Strengthened

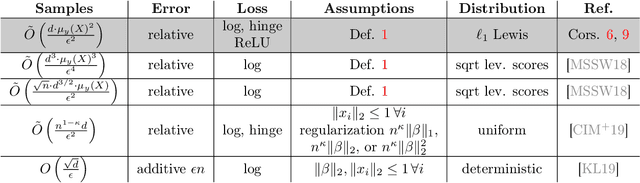
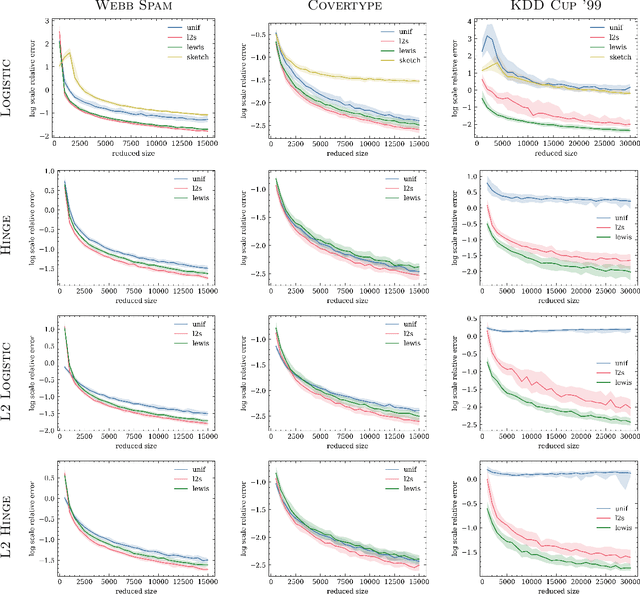
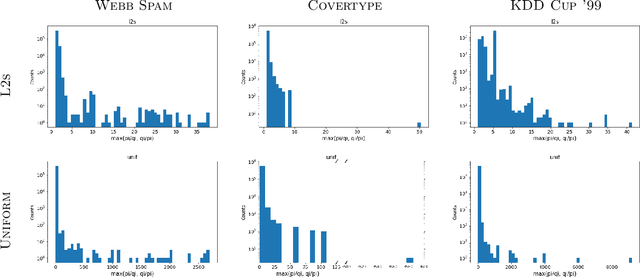
We give relative error coresets for training linear classifiers with a broad class of loss functions, including the logistic loss and hinge loss. Our construction achieves $(1\pm \epsilon)$ relative error with $\tilde O(d \cdot \mu_y(X)^2/\epsilon^2)$ points, where $\mu_y(X)$ is a natural complexity measure of the data matrix $X \in \mathbb{R}^{n \times d}$ and label vector $y \in \{-1,1\}^n$, introduced in by Munteanu et al. 2018. Our result is based on subsampling data points with probabilities proportional to their $\ell_1$ $Lewis$ $weights$. It significantly improves on existing theoretical bounds and performs well in practice, outperforming uniform subsampling along with other importance sampling methods. Our sampling distribution does not depend on the labels, so can be used for active learning. It also does not depend on the specific loss function, so a single coreset can be used in multiple training scenarios.