Causal Discovery-Driven Change Point Detection in Time Series

Change point detection in time series seeks to identify times when the probability distribution of time series changes. It is widely applied in many areas, such as human-activity sensing and medical science. In the context of multivariate time series, this typically involves examining the joint distribution of high-dimensional data: If any one variable changes, the whole time series is assumed to have changed. However, in practical applications, we may be interested only in certain components of the time series, exploring abrupt changes in their distributions in the presence of other time series. Here, assuming an underlying structural causal model that governs the time-series data generation, we address this problem by proposing a two-stage non-parametric algorithm that first learns parts of the causal structure through constraint-based discovery methods. The algorithm then uses conditional relative Pearson divergence estimation to identify the change points. The conditional relative Pearson divergence quantifies the distribution disparity between consecutive segments in the time series, while the causal discovery method enables a focus on the causal mechanism, facilitating access to independent and identically distributed (IID) samples. Theoretically, the typical assumption of samples being IID in conventional change point detection methods can be relaxed based on the Causal Markov Condition. Through experiments on both synthetic and real-world datasets, we validate the correctness and utility of our approach.

Causal Discovery in Semi-Stationary Time Series

Discovering causal relations from observational time series without making the stationary assumption is a significant challenge. In practice, this challenge is common in many areas, such as retail sales, transportation systems, and medical science. Here, we consider this problem for a class of non-stationary time series. The structural causal model (SCM) of this type of time series, called the semi-stationary time series, exhibits that a finite number of different causal mechanisms occur sequentially and periodically across time. This model holds considerable practical utility because it can represent periodicity, including common occurrences such as seasonality and diurnal variation. We propose a constraint-based, non-parametric algorithm for discovering causal relations in this setting. The resulting algorithm, PCMCI$_{\Omega}$, can capture the alternating and recurring changes in the causal mechanisms and then identify the underlying causal graph with conditional independence (CI) tests. We show that this algorithm is sound in identifying causal relations on discrete time series. We validate the algorithm with extensive experiments on continuous and discrete simulated data. We also apply our algorithm to a real-world climate dataset.

Limits of Approximating the Median Treatment Effect

Average Treatment Effect (ATE) estimation is a well-studied problem in causal inference. However, it does not necessarily capture the heterogeneity in the data, and several approaches have been proposed to tackle the issue, including estimating the Quantile Treatment Effects. In the finite population setting containing $n$ individuals, with treatment and control values denoted by the potential outcome vectors $\mathbf{a}, \mathbf{b}$, much of the prior work focused on estimating median$(\mathbf{a}) -$ median$(\mathbf{b})$, where median($\mathbf x$) denotes the median value in the sorted ordering of all the values in vector $\mathbf x$. It is known that estimating the difference of medians is easier than the desired estimand of median$(\mathbf{a-b})$, called the Median Treatment Effect (MTE). The fundamental problem of causal inference -- for every individual $i$, we can only observe one of the potential outcome values, i.e., either the value $a_i$ or $b_i$, but not both, makes estimating MTE particularly challenging. In this work, we argue that MTE is not estimable and detail a novel notion of approximation that relies on the sorted order of the values in $\mathbf{a-b}$. Next, we identify a quantity called variability that exactly captures the complexity of MTE estimation. By drawing connections to instance-optimality studied in theoretical computer science, we show that every algorithm for estimating the MTE obtains an approximation error that is no better than the error of an algorithm that computes variability. Finally, we provide a simple linear time algorithm for computing the variability exactly. Unlike much prior work, a particular highlight of our work is that we make no assumptions about how the potential outcome vectors are generated or how they are correlated, except that the potential outcome values are $k$-ary, i.e., take one of $k$ discrete values.

Continuous Treatment Effects with Surrogate Outcomes

In many real-world causal inference applications, the primary outcomes (labels) are often partially missing, especially if they are expensive or difficult to collect. If the missingness depends on covariates (i.e., missingness is not completely at random), analyses based on fully-observed samples alone may be biased. Incorporating surrogates, which are fully observed post-treatment variables related to the primary outcome, can improve estimation in this case. In this paper, we study the role of surrogates in estimating continuous treatment effects and propose a doubly robust method to efficiently incorporate surrogates in the analysis, which uses both labeled and unlabeled data and does not suffer from the above selection bias problem. Importantly, we establish asymptotic normality of the proposed estimator and show possible improvements on the variance compared with methods that solely use labeled data. Extensive simulations show our methods enjoy appealing empirical performance.

Sample Constrained Treatment Effect Estimation

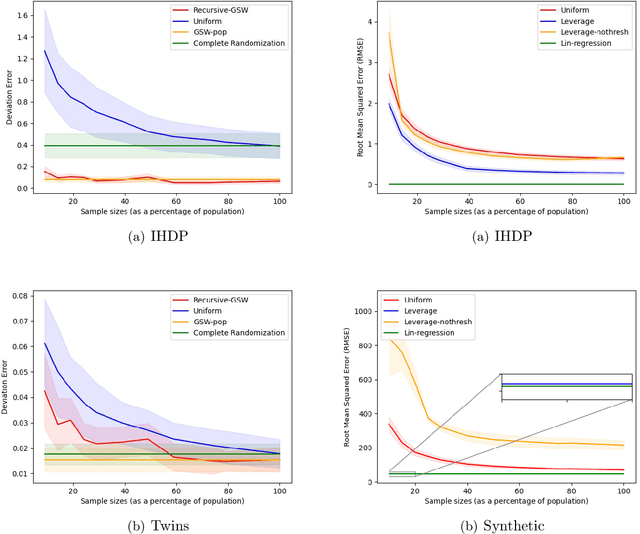
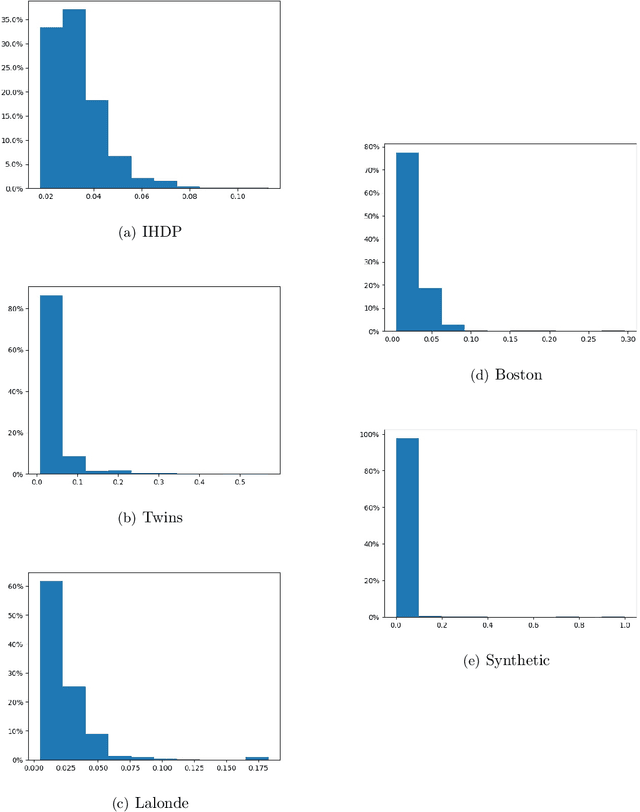
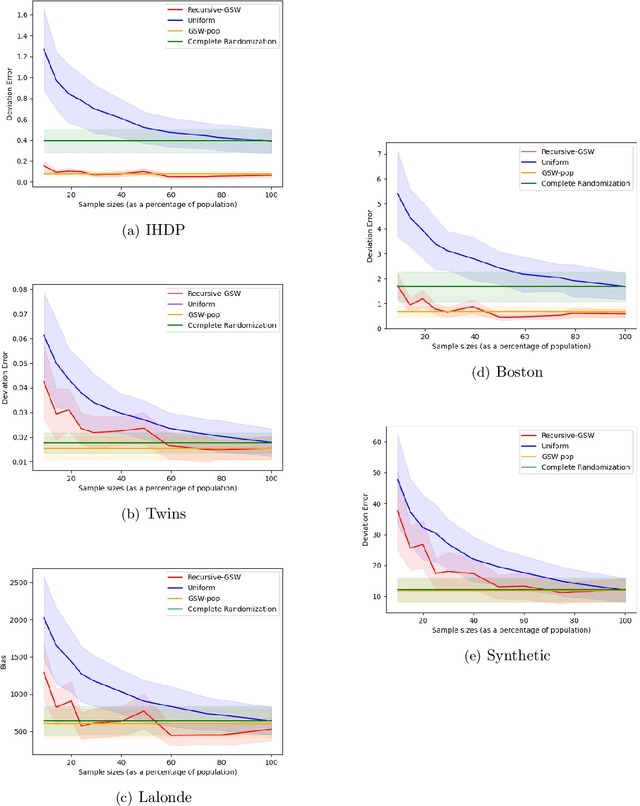
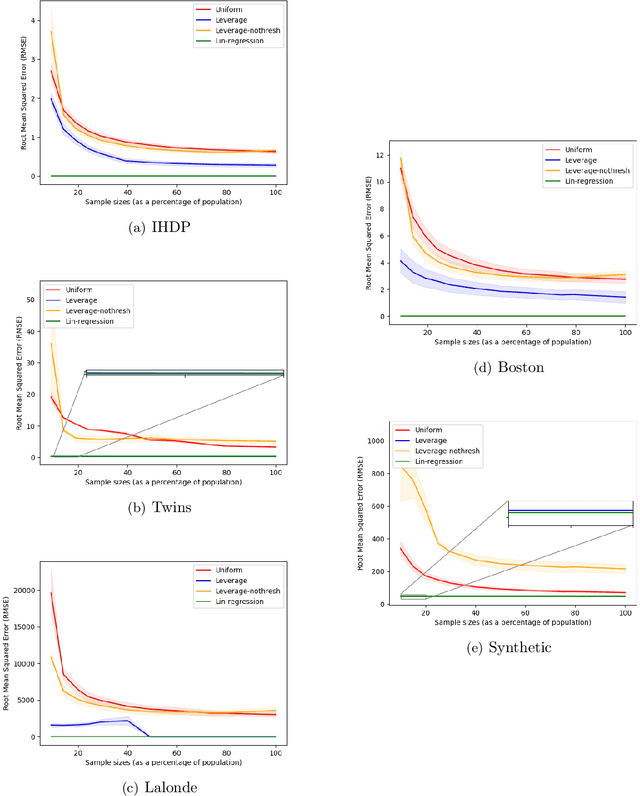
Treatment effect estimation is a fundamental problem in causal inference. We focus on designing efficient randomized controlled trials, to accurately estimate the effect of some treatment on a population of $n$ individuals. In particular, we study sample-constrained treatment effect estimation, where we must select a subset of $s \ll n$ individuals from the population to experiment on. This subset must be further partitioned into treatment and control groups. Algorithms for partitioning the entire population into treatment and control groups, or for choosing a single representative subset, have been well-studied. The key challenge in our setting is jointly choosing a representative subset and a partition for that set. We focus on both individual and average treatment effect estimation, under a linear effects model. We give provably efficient experimental designs and corresponding estimators, by identifying connections to discrepancy minimization and leverage-score-based sampling used in randomized numerical linear algebra. Our theoretical results obtain a smooth transition to known guarantees when $s$ equals the population size. We also empirically demonstrate the performance of our algorithms.

Collaborative Causal Discovery with Atomic Interventions

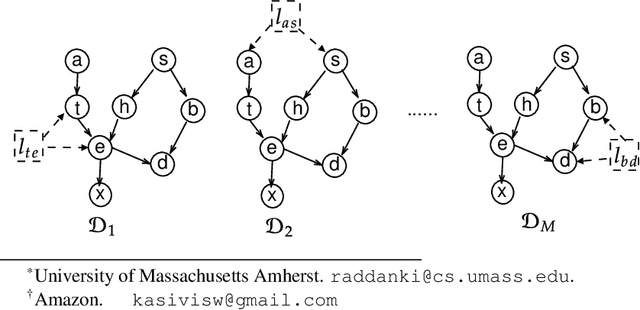
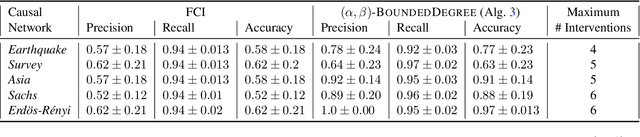
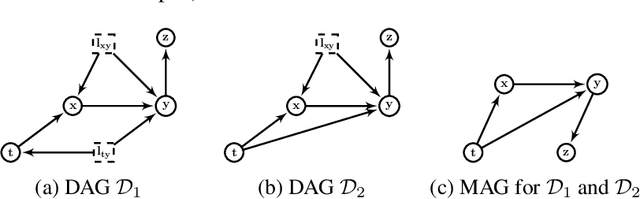
We introduce a new Collaborative Causal Discovery problem, through which we model a common scenario in which we have multiple independent entities each with their own causal graph, and the goal is to simultaneously learn all these causal graphs. We study this problem without the causal sufficiency assumption, using Maximal Ancestral Graphs (MAG) to model the causal graphs, and assuming that we have the ability to actively perform independent single vertex (or atomic) interventions on the entities. If the $M$ underlying (unknown) causal graphs of the entities satisfy a natural notion of clustering, we give algorithms that leverage this property and recovers all the causal graphs using roughly logarithmic in $M$ number of atomic interventions per entity. These are significantly fewer than $n$ atomic interventions per entity required to learn each causal graph separately, where $n$ is the number of observable nodes in the causal graph. We complement our results with a lower bound and discuss various extensions of our collaborative setting.

How to Design Robust Algorithms using Noisy Comparison Oracle

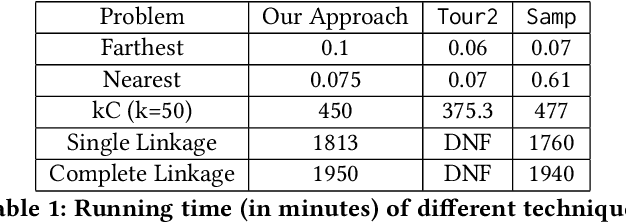
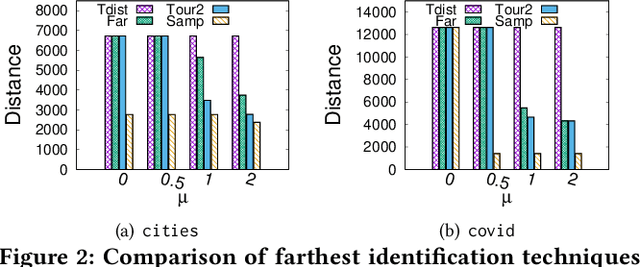
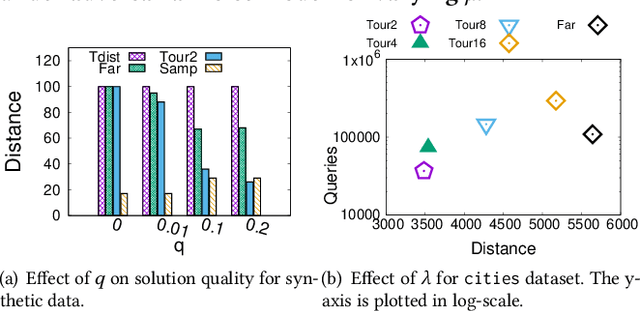
Metric based comparison operations such as finding maximum, nearest and farthest neighbor are fundamental to studying various clustering techniques such as $k$-center clustering and agglomerative hierarchical clustering. These techniques crucially rely on accurate estimation of pairwise distance between records. However, computing exact features of the records, and their pairwise distances is often challenging, and sometimes not possible. We circumvent this challenge by leveraging weak supervision in the form of a comparison oracle that compares the relative distance between the queried points such as `Is point u closer to v or w closer to x?'. However, it is possible that some queries are easier to answer than others using a comparison oracle. We capture this by introducing two different noise models called adversarial and probabilistic noise. In this paper, we study various problems that include finding maximum, nearest/farthest neighbor search under these noise models. Building upon the techniques we develop for these comparison operations, we give robust algorithms for k-center clustering and agglomerative hierarchical clustering. We prove that our algorithms achieve good approximation guarantees with a high probability and analyze their query complexity. We evaluate the effectiveness and efficiency of our techniques empirically on various real-world datasets.

Intervention Efficient Algorithms for Approximate Learning of Causal Graphs

We study the problem of learning the causal relationships between a set of observed variables in the presence of latents, while minimizing the cost of interventions on the observed variables. We assume access to an undirected graph $G$ on the observed variables whose edges represent either all direct causal relationships or, less restrictively, a superset of causal relationships (identified, e.g., via conditional independence tests or a domain expert). Our goal is to recover the directions of all causal or ancestral relations in $G$, via a minimum cost set of interventions. It is known that constructing an exact minimum cost intervention set for an arbitrary graph $G$ is NP-hard. We further argue that, conditioned on the hardness of approximate graph coloring, no polynomial time algorithm can achieve an approximation factor better than $\Theta(\log n)$, where $n$ is the number of observed variables in $G$. To overcome this limitation, we introduce a bi-criteria approximation goal that lets us recover the directions of all but $\epsilon n^2$ edges in $G$, for some specified error parameter $\epsilon > 0$. Under this relaxed goal, we give polynomial time algorithms that achieve intervention cost within a small constant factor of the optimal. Our algorithms combine work on efficient intervention design and the design of low-cost separating set systems, with ideas from the literature on graph property testing.

Efficient Intervention Design for Causal Discovery with Latents

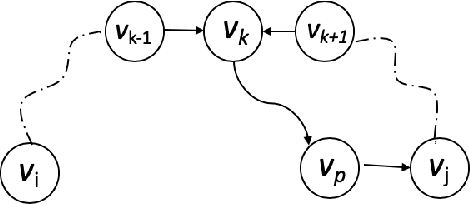
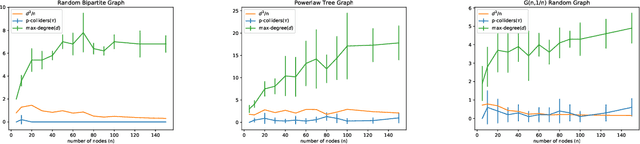
We consider recovering a causal graph in presence of latent variables, where we seek to minimize the cost of interventions used in the recovery process. We consider two intervention cost models: (1) a linear cost model where the cost of an intervention on a subset of variables has a linear form, and (2) an identity cost model where the cost of an intervention is the same, regardless of what variables it is on, i.e., the goal is just to minimize the number of interventions. Under the linear cost model, we give an algorithm to identify the ancestral relations of the underlying causal graph, achieving within a $2$-factor of the optimal intervention cost. This approximation factor can be improved to $1+\epsilon$ for any $\epsilon > 0$ under some mild restrictions. Under the identity cost model, we bound the number of interventions needed to recover the entire causal graph, including the latent variables, using a parameterization of the causal graph through a special type of colliders. In particular, we introduce the notion of $p$-colliders, that are colliders between pair of nodes arising from a specific type of conditioning in the causal graph, and provide an upper bound on the number of interventions as a function of the maximum number of $p$-colliders between any two nodes in the causal graph.

Snomed2Vec: Random Walk and Poincaré Embeddings of a Clinical Knowledge Base for Healthcare Analytics

Representation learning methods that transform encoded data (e.g., diagnosis and drug codes) into continuous vector spaces (i.e., vector embeddings) are critical for the application of deep learning in healthcare. Initial work in this area explored the use of variants of the word2vec algorithm to learn embeddings for medical concepts from electronic health records or medical claims datasets. We propose learning embeddings for medical concepts by using graph-based representation learning methods on SNOMED-CT, a widely popular knowledge graph in the healthcare domain with numerous operational and research applications. Current work presents an empirical analysis of various embedding methods, including the evaluation of their performance on multiple tasks of biomedical relevance (node classification, link prediction, and patient state prediction). Our results show that concept embeddings derived from the SNOMED-CT knowledge graph significantly outperform state-of-the-art embeddings, showing 5-6x improvement in ``concept similarity" and 6-20\% improvement in patient diagnosis.