Analysis of the MICCAI Brain Tumor Segmentation -- Metastases (BraTS-METS) 2025 Lighthouse Challenge: Brain Metastasis Segmentation on Pre- and Post-treatment MRI

Despite continuous advancements in cancer treatment, brain metastatic disease remains a significant complication of primary cancer and is associated with an unfavorable prognosis. One approach for improving diagnosis, management, and outcomes is to implement algorithms based on artificial intelligence for the automated segmentation of both pre- and post-treatment MRI brain images. Such algorithms rely on volumetric criteria for lesion identification and treatment response assessment, which are still not available in clinical practice. Therefore, it is critical to establish tools for rapid volumetric segmentations methods that can be translated to clinical practice and that are trained on high quality annotated data. The BraTS-METS 2025 Lighthouse Challenge aims to address this critical need by establishing inter-rater and intra-rater variability in dataset annotation by generating high quality annotated datasets from four individual instances of segmentation by neuroradiologists while being recorded on video (two instances doing "from scratch" and two instances after AI pre-segmentation). This high-quality annotated dataset will be used for testing phase in 2025 Lighthouse challenge and will be publicly released at the completion of the challenge. The 2025 Lighthouse challenge will also release the 2023 and 2024 segmented datasets that were annotated using an established pipeline of pre-segmentation, student annotation, two neuroradiologists checking, and one neuroradiologist finalizing the process. It builds upon its previous edition by including post-treatment cases in the dataset. Using these high-quality annotated datasets, the 2025 Lighthouse challenge plans to test benchmark algorithms for automated segmentation of pre-and post-treatment brain metastases (BM), trained on diverse and multi-institutional datasets of MRI images obtained from patients with brain metastases.

Data subsampling for Poisson regression with pth-root-link

We develop and analyze data subsampling techniques for Poisson regression, the standard model for count data $y\in\mathbb{N}$. In particular, we consider the Poisson generalized linear model with ID- and square root-link functions. We consider the method of coresets, which are small weighted subsets that approximate the loss function of Poisson regression up to a factor of $1\pm\varepsilon$. We show $\Omega(n)$ lower bounds against coresets for Poisson regression that continue to hold against arbitrary data reduction techniques up to logarithmic factors. By introducing a novel complexity parameter and a domain shifting approach, we show that sublinear coresets with $1\pm\varepsilon$ approximation guarantee exist when the complexity parameter is small. In particular, the dependence on the number of input points can be reduced to polylogarithmic. We show that the dependence on other input parameters can also be bounded sublinearly, though not always logarithmically. In particular, we show that the square root-link admits an $O(\log(y_{\max}))$ dependence, where $y_{\max}$ denotes the largest count presented in the data, while the ID-link requires a $\Theta(\sqrt{y_{\max}/\log(y_{\max})})$ dependence. As an auxiliary result for proving the tightness of the bound with respect to $y_{\max}$ in the case of the ID-link, we show an improved bound on the principal branch of the Lambert $W_0$ function, which may be of independent interest. We further show the limitations of our analysis when $p$th degree root-link functions for $p\geq 3$ are considered, which indicate that other analytical or computational methods would be required if such a generalization is even possible.

Scalable Learning of Item Response Theory Models

Item Response Theory (IRT) models aim to assess latent abilities of $n$ examinees along with latent difficulty characteristics of $m$ test items from categorical data that indicates the quality of their corresponding answers. Classical psychometric assessments are based on a relatively small number of examinees and items, say a class of $200$ students solving an exam comprising $10$ problems. More recent global large scale assessments such as PISA, or internet studies, may lead to significantly increased numbers of participants. Additionally, in the context of Machine Learning where algorithms take the role of examinees and data analysis problems take the role of items, both $n$ and $m$ may become very large, challenging the efficiency and scalability of computations. To learn the latent variables in IRT models from large data, we leverage the similarity of these models to logistic regression, which can be approximated accurately using small weighted subsets called coresets. We develop coresets for their use in alternating IRT training algorithms, facilitating scalable learning from large data.

Optimal Sketching Bounds for Sparse Linear Regression

We study oblivious sketching for $k$-sparse linear regression under various loss functions such as an $\ell_p$ norm, or from a broad class of hinge-like loss functions, which includes the logistic and ReLU losses. We show that for sparse $\ell_2$ norm regression, there is a distribution over oblivious sketches with $\Theta(k\log(d/k)/\varepsilon^2)$ rows, which is tight up to a constant factor. This extends to $\ell_p$ loss with an additional additive $O(k\log(k/\varepsilon)/\varepsilon^2)$ term in the upper bound. This establishes a surprising separation from the related sparse recovery problem, which is an important special case of sparse regression. For this problem, under the $\ell_2$ norm, we observe an upper bound of $O(k \log (d)/\varepsilon + k\log(k/\varepsilon)/\varepsilon^2)$ rows, showing that sparse recovery is strictly easier to sketch than sparse regression. For sparse regression under hinge-like loss functions including sparse logistic and sparse ReLU regression, we give the first known sketching bounds that achieve $o(d)$ rows showing that $O(\mu^2 k\log(\mu n d/\varepsilon)/\varepsilon^2)$ rows suffice, where $\mu$ is a natural complexity parameter needed to obtain relative error bounds for these loss functions. We again show that this dimension is tight, up to lower order terms and the dependence on $\mu$. Finally, we show that similar sketching bounds can be achieved for LASSO regression, a popular convex relaxation of sparse regression, where one aims to minimize $\|Ax-b\|_2^2+\lambda\|x\|_1$ over $x\in\mathbb{R}^d$. We show that sketching dimension $O(\log(d)/(\lambda \varepsilon)^2)$ suffices and that the dependence on $d$ and $\lambda$ is tight.

Almost Linear Constant-Factor Sketching for $\ell_1$ and Logistic Regression

We improve upon previous oblivious sketching and turnstile streaming results for $\ell_1$ and logistic regression, giving a much smaller sketching dimension achieving $O(1)$-approximation and yielding an efficient optimization problem in the sketch space. Namely, we achieve for any constant $c>0$ a sketching dimension of $\tilde{O}(d^{1+c})$ for $\ell_1$ regression and $\tilde{O}(\mu d^{1+c})$ for logistic regression, where $\mu$ is a standard measure that captures the complexity of compressing the data. For $\ell_1$-regression our sketching dimension is near-linear and improves previous work which either required $\Omega(\log d)$-approximation with this sketching dimension, or required a larger $\operatorname{poly}(d)$ number of rows. Similarly, for logistic regression previous work had worse $\operatorname{poly}(\mu d)$ factors in its sketching dimension. We also give a tradeoff that yields a $1+\varepsilon$ approximation in input sparsity time by increasing the total size to $(d\log(n)/\varepsilon)^{O(1/\varepsilon)}$ for $\ell_1$ and to $(\mu d\log(n)/\varepsilon)^{O(1/\varepsilon)}$ for logistic regression. Finally, we show that our sketch can be extended to approximate a regularized version of logistic regression where the data-dependent regularizer corresponds to the variance of the individual logistic losses.

Bounding the Width of Neural Networks via Coupled Initialization -- A Worst Case Analysis

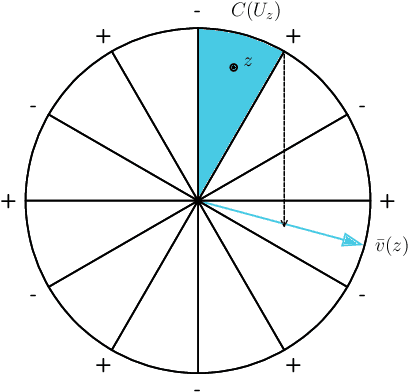
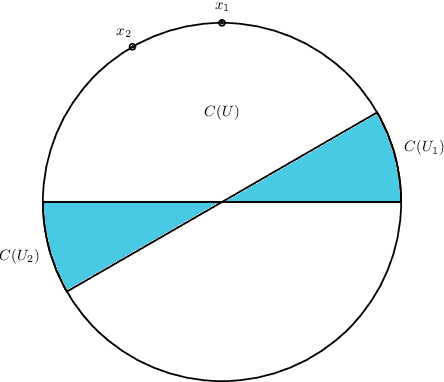
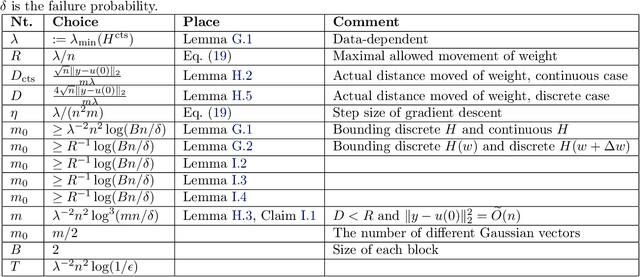
A common method in training neural networks is to initialize all the weights to be independent Gaussian vectors. We observe that by instead initializing the weights into independent pairs, where each pair consists of two identical Gaussian vectors, we can significantly improve the convergence analysis. While a similar technique has been studied for random inputs [Daniely, NeurIPS 2020], it has not been analyzed with arbitrary inputs. Using this technique, we show how to significantly reduce the number of neurons required for two-layer ReLU networks, both in the under-parameterized setting with logistic loss, from roughly $\gamma^{-8}$ [Ji and Telgarsky, ICLR 2020] to $\gamma^{-2}$, where $\gamma$ denotes the separation margin with a Neural Tangent Kernel, as well as in the over-parameterized setting with squared loss, from roughly $n^4$ [Song and Yang, 2019] to $n^2$, implicitly also improving the recent running time bound of [Brand, Peng, Song and Weinstein, ITCS 2021]. For the under-parameterized setting we also prove new lower bounds that improve upon prior work, and that under certain assumptions, are best possible.

$p$-Generalized Probit Regression and Scalable Maximum Likelihood Estimation via Sketching and Coresets

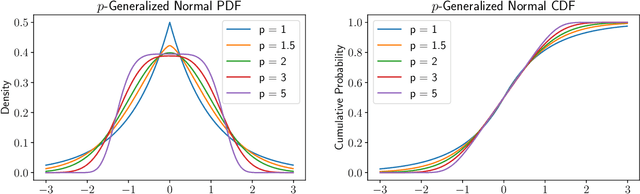
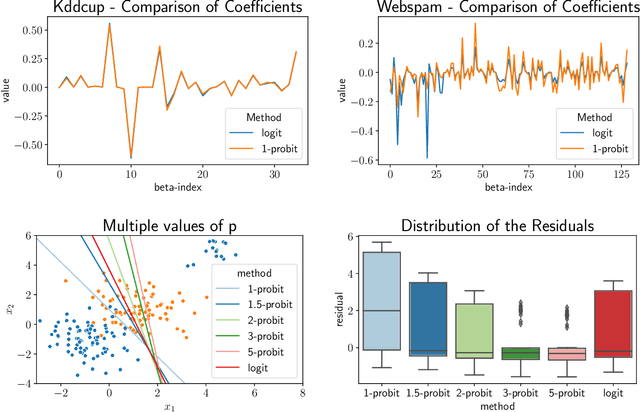
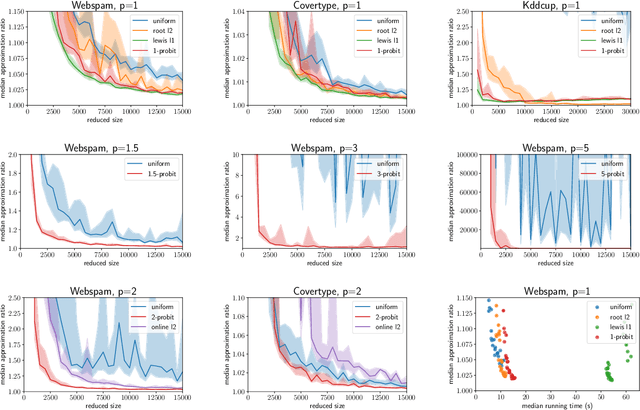
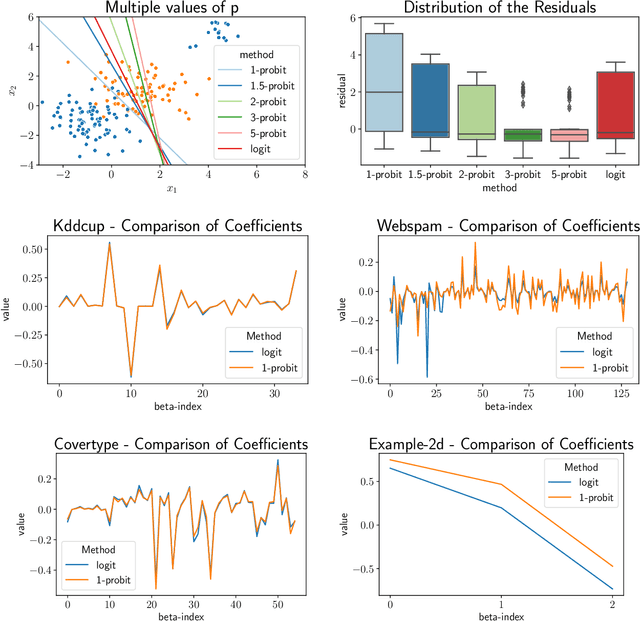
We study the $p$-generalized probit regression model, which is a generalized linear model for binary responses. It extends the standard probit model by replacing its link function, the standard normal cdf, by a $p$-generalized normal distribution for $p\in[1, \infty)$. The $p$-generalized normal distributions \citep{Sub23} are of special interest in statistical modeling because they fit much more flexibly to data. Their tail behavior can be controlled by choice of the parameter $p$, which influences the model's sensitivity to outliers. Special cases include the Laplace, the Gaussian, and the uniform distributions. We further show how the maximum likelihood estimator for $p$-generalized probit regression can be approximated efficiently up to a factor of $(1+\varepsilon)$ on large data by combining sketching techniques with importance subsampling to obtain a small data summary called coreset.

Oblivious sketching for logistic regression

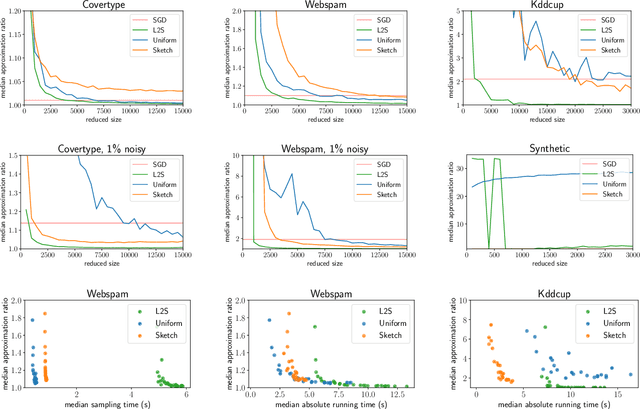
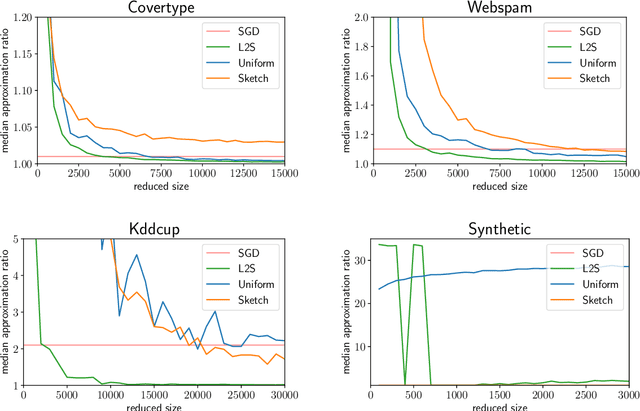
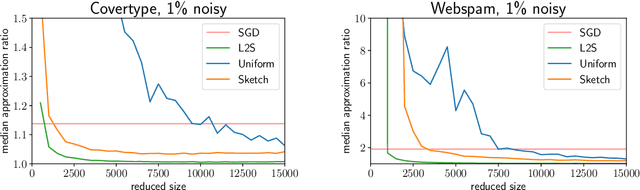
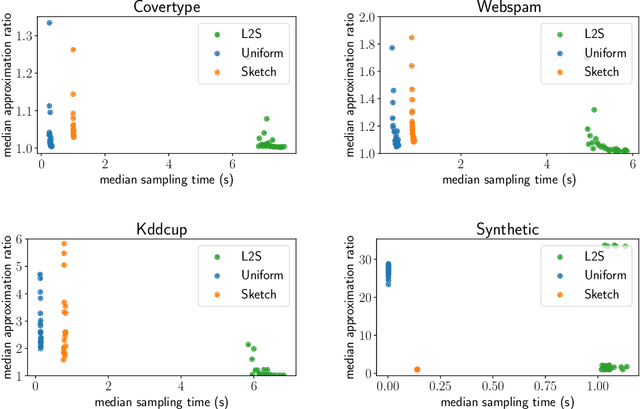
What guarantees are possible for solving logistic regression in one pass over a data stream? To answer this question, we present the first data oblivious sketch for logistic regression. Our sketch can be computed in input sparsity time over a turnstile data stream and reduces the size of a $d$-dimensional data set from $n$ to only $\operatorname{poly}(\mu d\log n)$ weighted points, where $\mu$ is a useful parameter which captures the complexity of compressing the data. Solving (weighted) logistic regression on the sketch gives an $O(\log n)$-approximation to the original problem on the full data set. We also show how to obtain an $O(1)$-approximation with slight modifications. Our sketches are fast, simple, easy to implement, and our experiments demonstrate their practicality.

Random projections and sampling algorithms for clustering of high-dimensional polygonal curves

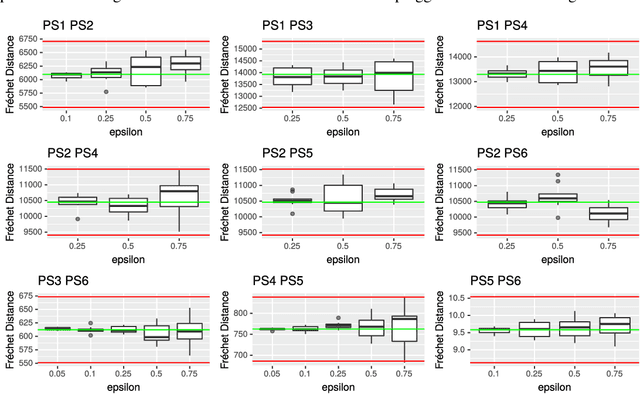
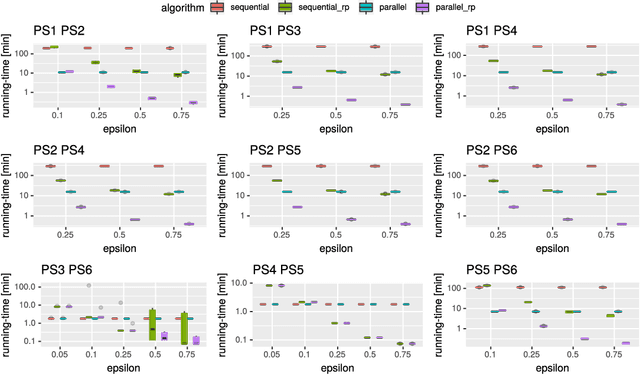
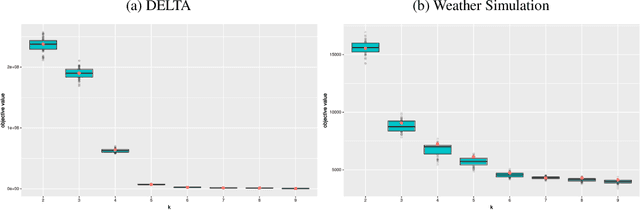
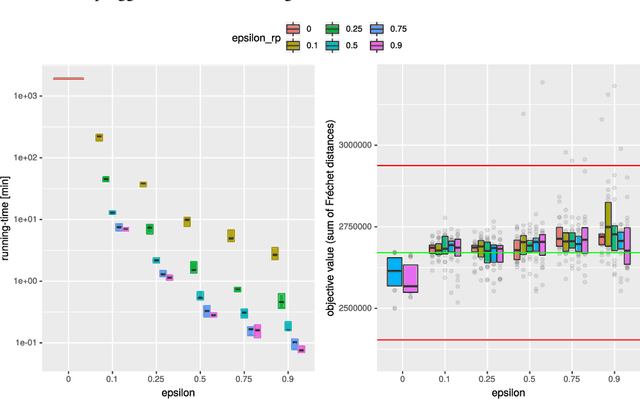
We study the center and median clustering problems for high-dimensional polygonal curves with finite but unbounded complexity. We tackle the computational issue that arises from the high number of dimensions by defining a Johnson-Lindenstrauss projection for polygonal curves. We analyze the resulting error in terms of the Fr\'echet distance, which is a natural dissimilarity measure for curves. Our algorithms for the median clustering achieve sublinear dependency on the number of input curves via subsampling. For the center clustering we utilize Buchin et al. (2019a) algorithm that achieves linear running-time in the number of input curves. We evaluate our results empirically utilizing a fast, CUDA-parallelized variant of the Alt and Godau algorithm for the Fr\'echet distance. Our experiments show that our clustering algorithms have fast and accurate practical implementations that yield meaningful results on real world data from various physical domains.

Probabilistic smallest enclosing ball in high dimensions via subgradient sampling

We study a variant of the median problem for a collection of point sets in high dimensions. This generalizes the geometric median as well as the (probabilistic) smallest enclosing ball (pSEB) problems. Our main objective and motivation is to improve the previously best algorithm for the pSEB problem by reducing its exponential dependence on the dimension to linear. This is achieved via a novel combination of sampling techniques for clustering problems in metric spaces with the framework of stochastic subgradient descent. As a result, the algorithm becomes applicable to shape fitting problems in Hilbert spaces of unbounded dimension via kernel functions. We present an exemplary application by extending the support vector data description (SVDD) shape fitting method to the probabilistic case. This is done by simulating the pSEB algorithm implicitly in the feature space induced by the kernel function.