ScaleViz: Scaling Visualization Recommendation Models on Large Data

Automated visualization recommendations (vis-rec) help users to derive crucial insights from new datasets. Typically, such automated vis-rec models first calculate a large number of statistics from the datasets and then use machine-learning models to score or classify multiple visualizations choices to recommend the most effective ones, as per the statistics. However, state-of-the art models rely on very large number of expensive statistics and therefore using such models on large datasets become infeasible due to prohibitively large computational time, limiting the effectiveness of such techniques to most real world complex and large datasets. In this paper, we propose a novel reinforcement-learning (RL) based framework that takes a given vis-rec model and a time-budget from the user and identifies the best set of input statistics that would be most effective while generating the visual insights within a given time budget, using the given model. Using two state-of-the-art vis-rec models applied on three large real-world datasets, we show the effectiveness of our technique in significantly reducing time-to visualize with very small amount of introduced error. Our approach is about 10X times faster compared to the baseline approaches that introduce similar amounts of error.

Electra: Conditional Generative Model based Predicate-Aware Query Approximation

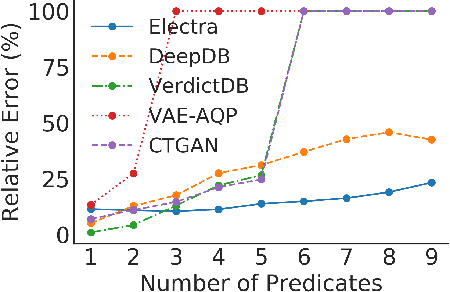
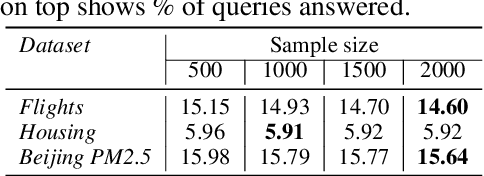
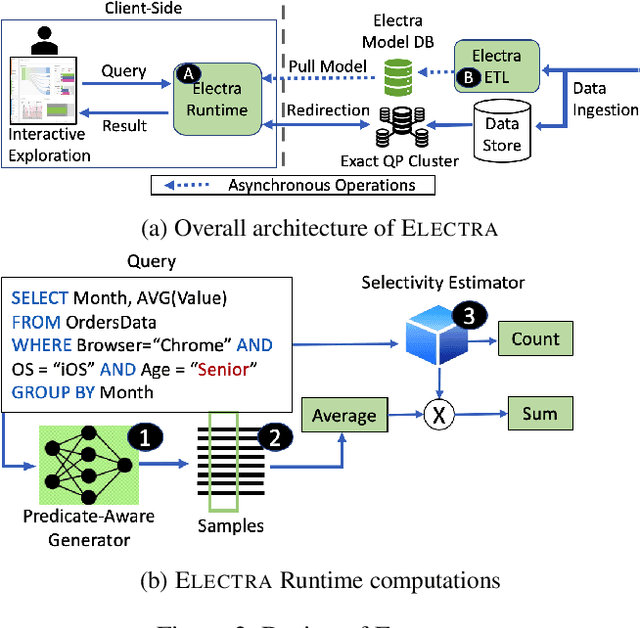
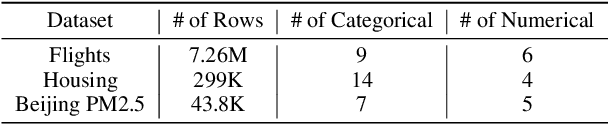
The goal of Approximate Query Processing (AQP) is to provide very fast but "accurate enough" results for costly aggregate queries thereby improving user experience in interactive exploration of large datasets. Recently proposed Machine-Learning based AQP techniques can provide very low latency as query execution only involves model inference as compared to traditional query processing on database clusters. However, with increase in the number of filtering predicates(WHERE clauses), the approximation error significantly increases for these methods. Analysts often use queries with a large number of predicates for insights discovery. Thus, maintaining low approximation error is important to prevent analysts from drawing misleading conclusions. In this paper, we propose ELECTRA, a predicate-aware AQP system that can answer analytics-style queries with a large number of predicates with much smaller approximation errors. ELECTRA uses a conditional generative model that learns the conditional distribution of the data and at runtime generates a small (~1000 rows) but representative sample, on which the query is executed to compute the approximate result. Our evaluations with four different baselines on three real-world datasets show that ELECTRA provides lower AQP error for large number of predicates compared to baselines.

Almost Optimal Universal Lower Bound for Learning Causal DAGs with Atomic Interventions

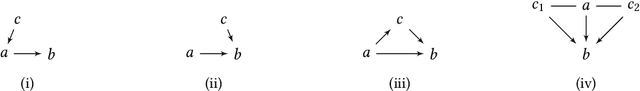
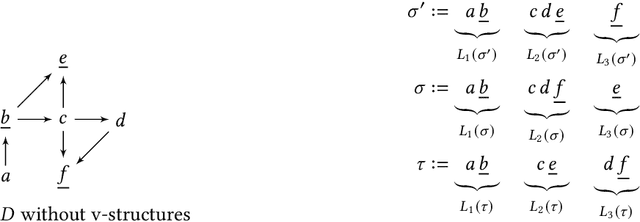
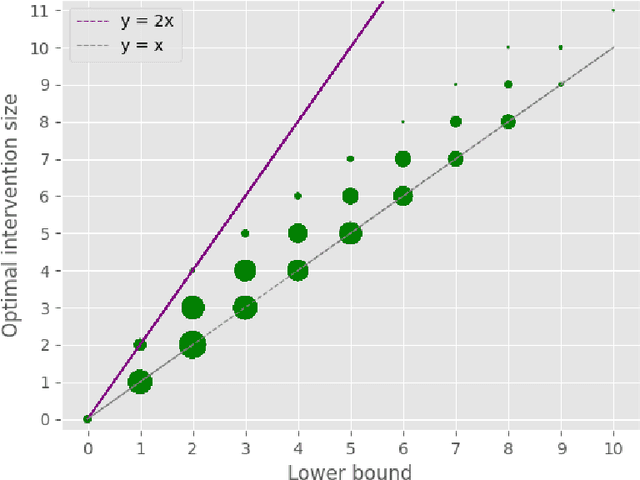
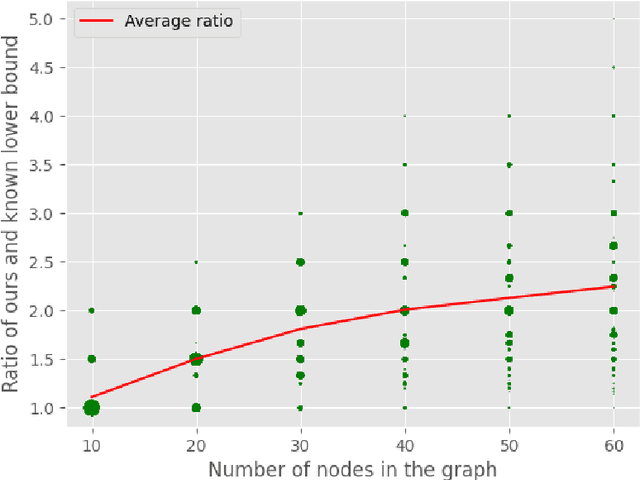
A well-studied challenge that arises in the structure learning problem of causal directed acyclic graphs (DAG) is that using observational data, one can only learn the graph up to a "Markov equivalence class" (MEC). The remaining undirected edges have to be oriented using interventions, which can be very expensive to perform in applications. Thus, the problem of minimizing the number of interventions needed to fully orient the MEC has received a lot of recent attention, and is also the focus of this work. We prove two main results. The first is a new universal lower bound on the number of atomic interventions that any algorithm (whether active or passive) would need to perform in order to orient a given MEC. Our second result shows that this bound is, in fact, within a factor of two of the size of the smallest set of atomic interventions that can orient the MEC. Our lower bound is provably better than previously known lower bounds. The proof of our lower bound is based on the new notion of clique-block shared-parents (CBSP) orderings, which are topological orderings of DAGs without v-structures and satisfy certain special properties. Further, using simulations on synthetic graphs and by giving examples of special graph families, we show that our bound is often significantly better.