Online Adaptive Mahalanobis Distance Estimation

Mahalanobis metrics are widely used in machine learning in conjunction with methods like $k$-nearest neighbors, $k$-means clustering, and $k$-medians clustering. Despite their importance, there has not been any prior work on applying sketching techniques to speed up algorithms for Mahalanobis metrics. In this paper, we initiate the study of dimension reduction for Mahalanobis metrics. In particular, we provide efficient data structures for solving the Approximate Distance Estimation (ADE) problem for Mahalanobis distances. We first provide a randomized Monte Carlo data structure. Then, we show how we can adapt it to provide our main data structure which can handle sequences of \textit{adaptive} queries and also online updates to both the Mahalanobis metric matrix and the data points, making it amenable to be used in conjunction with prior algorithms for online learning of Mahalanobis metrics.

Adaptive and Dynamic Multi-Resolution Hashing for Pairwise Summations

In this paper, we propose Adam-Hash: an adaptive and dynamic multi-resolution hashing data-structure for fast pairwise summation estimation. Given a data-set $X \subset \mathbb{R}^d$, a binary function $f:\mathbb{R}^d\times \mathbb{R}^d\to \mathbb{R}$, and a point $y \in \mathbb{R}^d$, the Pairwise Summation Estimate $\mathrm{PSE}_X(y) := \frac{1}{|X|} \sum_{x \in X} f(x,y)$. For any given data-set $X$, we need to design a data-structure such that given any query point $y \in \mathbb{R}^d$, the data-structure approximately estimates $\mathrm{PSE}_X(y)$ in time that is sub-linear in $|X|$. Prior works on this problem have focused exclusively on the case where the data-set is static, and the queries are independent. In this paper, we design a hashing-based PSE data-structure which works for the more practical \textit{dynamic} setting in which insertions, deletions, and replacements of points are allowed. Moreover, our proposed Adam-Hash is also robust to adaptive PSE queries, where an adversary can choose query $q_j \in \mathbb{R}^d$ depending on the output from previous queries $q_1, q_2, \dots, q_{j-1}$.

Dynamic Tensor Product Regression

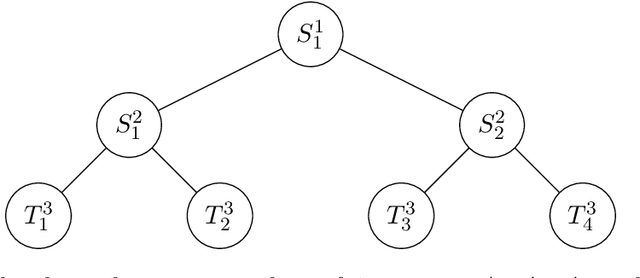
In this work, we initiate the study of \emph{Dynamic Tensor Product Regression}. One has matrices $A_1\in \mathbb{R}^{n_1\times d_1},\ldots,A_q\in \mathbb{R}^{n_q\times d_q}$ and a label vector $b\in \mathbb{R}^{n_1\ldots n_q}$, and the goal is to solve the regression problem with the design matrix $A$ being the tensor product of the matrices $A_1, A_2, \dots, A_q$ i.e. $\min_{x\in \mathbb{R}^{d_1\ldots d_q}}~\|(A_1\otimes \ldots\otimes A_q)x-b\|_2$. At each time step, one matrix $A_i$ receives a sparse change, and the goal is to maintain a sketch of the tensor product $A_1\otimes\ldots \otimes A_q$ so that the regression solution can be updated quickly. Recomputing the solution from scratch for each round is very slow and so it is important to develop algorithms which can quickly update the solution with the new design matrix. Our main result is a dynamic tree data structure where any update to a single matrix can be propagated quickly throughout the tree. We show that our data structure can be used to solve dynamic versions of not only Tensor Product Regression, but also Tensor Product Spline regression (which is a generalization of ridge regression) and for maintaining Low Rank Approximations for the tensor product.

Online MAP Inference and Learning for Nonsymmetric Determinantal Point Processes

In this paper, we introduce the online and streaming MAP inference and learning problems for Non-symmetric Determinantal Point Processes (NDPPs) where data points arrive in an arbitrary order and the algorithms are constrained to use a single-pass over the data as well as sub-linear memory. The online setting has an additional requirement of maintaining a valid solution at any point in time. For solving these new problems, we propose algorithms with theoretical guarantees, evaluate them on several real-world datasets, and show that they give comparable performance to state-of-the-art offline algorithms that store the entire data in memory and take multiple passes over it.

Beyond Perturbation Stability: LP Recovery Guarantees for MAP Inference on Noisy Stable Instances

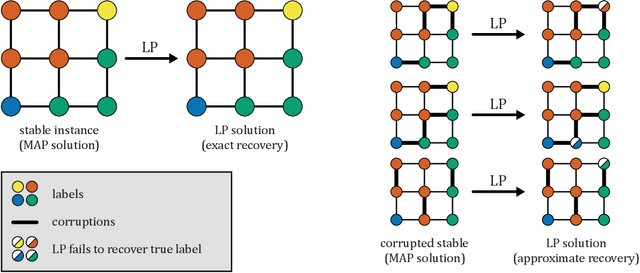
Several works have shown that perturbation stable instances of the MAP inference problem in Potts models can be solved exactly using a natural linear programming (LP) relaxation. However, most of these works give few (or no) guarantees for the LP solutions on instances that do not satisfy the relatively strict perturbation stability definitions. In this work, we go beyond these stability results by showing that the LP approximately recovers the MAP solution of a stable instance even after the instance is corrupted by noise. This "noisy stable" model realistically fits with practical MAP inference problems: we design an algorithm for finding "close" stable instances, and show that several real-world instances from computer vision have nearby instances that are perturbation stable. These results suggest a new theoretical explanation for the excellent performance of this LP relaxation in practice.

Improved Guarantees for k-means++ and k-means++ Parallel

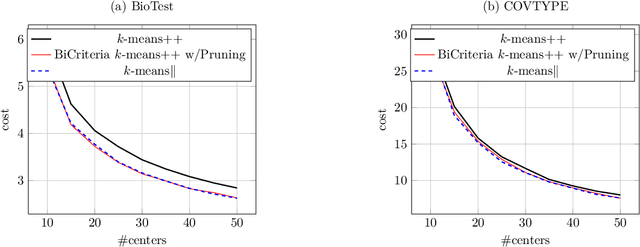
In this paper, we study k-means++ and k-means++ parallel, the two most popular algorithms for the classic k-means clustering problem. We provide novel analyses and show improved approximation and bi-criteria approximation guarantees for k-means++ and k-means++ parallel. Our results give a better theoretical justification for why these algorithms perform extremely well in practice. We also propose a new variant of k-means++ parallel algorithm (Exponential Race k-means++) that has the same approximation guarantees as k-means++.