Optimal Sketching Bounds for Sparse Linear Regression

We study oblivious sketching for $k$-sparse linear regression under various loss functions such as an $\ell_p$ norm, or from a broad class of hinge-like loss functions, which includes the logistic and ReLU losses. We show that for sparse $\ell_2$ norm regression, there is a distribution over oblivious sketches with $\Theta(k\log(d/k)/\varepsilon^2)$ rows, which is tight up to a constant factor. This extends to $\ell_p$ loss with an additional additive $O(k\log(k/\varepsilon)/\varepsilon^2)$ term in the upper bound. This establishes a surprising separation from the related sparse recovery problem, which is an important special case of sparse regression. For this problem, under the $\ell_2$ norm, we observe an upper bound of $O(k \log (d)/\varepsilon + k\log(k/\varepsilon)/\varepsilon^2)$ rows, showing that sparse recovery is strictly easier to sketch than sparse regression. For sparse regression under hinge-like loss functions including sparse logistic and sparse ReLU regression, we give the first known sketching bounds that achieve $o(d)$ rows showing that $O(\mu^2 k\log(\mu n d/\varepsilon)/\varepsilon^2)$ rows suffice, where $\mu$ is a natural complexity parameter needed to obtain relative error bounds for these loss functions. We again show that this dimension is tight, up to lower order terms and the dependence on $\mu$. Finally, we show that similar sketching bounds can be achieved for LASSO regression, a popular convex relaxation of sparse regression, where one aims to minimize $\|Ax-b\|_2^2+\lambda\|x\|_1$ over $x\in\mathbb{R}^d$. We show that sketching dimension $O(\log(d)/(\lambda \varepsilon)^2)$ suffices and that the dependence on $d$ and $\lambda$ is tight.

Coresets for Classification -- Simplified and Strengthened

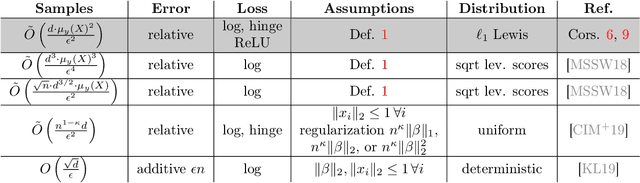
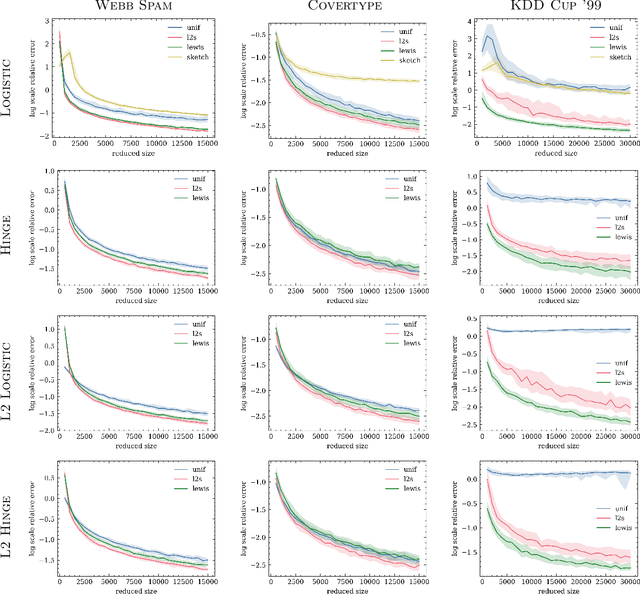
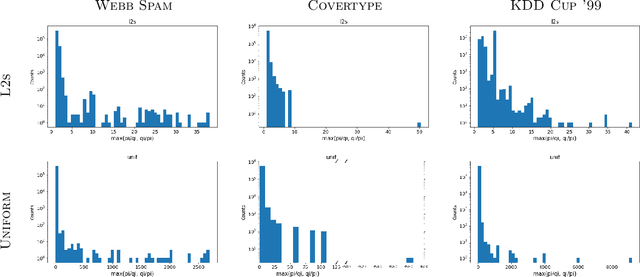
We give relative error coresets for training linear classifiers with a broad class of loss functions, including the logistic loss and hinge loss. Our construction achieves $(1\pm \epsilon)$ relative error with $\tilde O(d \cdot \mu_y(X)^2/\epsilon^2)$ points, where $\mu_y(X)$ is a natural complexity measure of the data matrix $X \in \mathbb{R}^{n \times d}$ and label vector $y \in \{-1,1\}^n$, introduced in by Munteanu et al. 2018. Our result is based on subsampling data points with probabilities proportional to their $\ell_1$ $Lewis$ $weights$. It significantly improves on existing theoretical bounds and performs well in practice, outperforming uniform subsampling along with other importance sampling methods. Our sampling distribution does not depend on the labels, so can be used for active learning. It also does not depend on the specific loss function, so a single coreset can be used in multiple training scenarios.

Efficient Second-Order Shape-Constrained Function Fitting

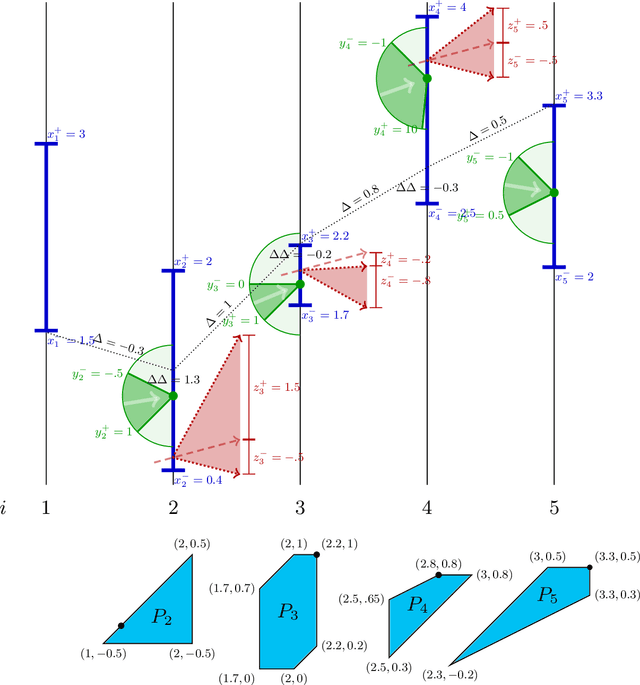
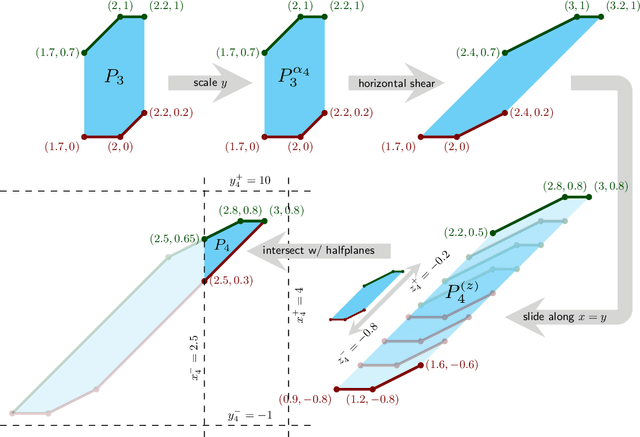
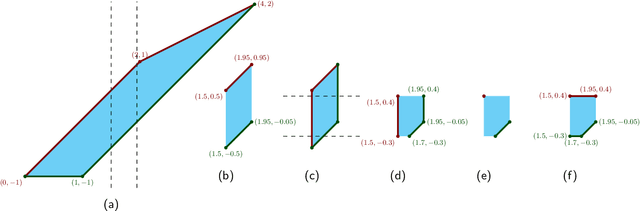
We give an algorithm to compute a one-dimensional shape-constrained function that best fits given data in weighted-$L_{\infty}$ norm. We give a single algorithm that works for a variety of commonly studied shape constraints including monotonicity, Lipschitz-continuity and convexity, and more generally, any shape constraint expressible by bounds on first- and/or second-order differences. Our algorithm computes an approximation with additive error $\varepsilon$ in $O\left(n \log \frac{U}{\varepsilon} \right)$ time, where $U$ captures the range of input values. We also give a simple greedy algorithm that runs in $O(n)$ time for the special case of unweighted $L_{\infty}$ convex regression. These are the first (near-)linear-time algorithms for second-order-constrained function fitting. To achieve these results, we use a novel geometric interpretation of the underlying dynamic programming problem. We further show that a generalization of the corresponding problems to directed acyclic graphs (DAGs) is as difficult as linear programming.

Agnostic Estimation of Mean and Covariance

We consider the problem of estimating the mean and covariance of a distribution from iid samples in $\mathbb{R}^n$, in the presence of an $\eta$ fraction of malicious noise; this is in contrast to much recent work where the noise itself is assumed to be from a distribution of known type. The agnostic problem includes many interesting special cases, e.g., learning the parameters of a single Gaussian (or finding the best-fit Gaussian) when $\eta$ fraction of data is adversarially corrupted, agnostically learning a mixture of Gaussians, agnostic ICA, etc. We present polynomial-time algorithms to estimate the mean and covariance with error guarantees in terms of information-theoretic lower bounds. As a corollary, we also obtain an agnostic algorithm for Singular Value Decomposition.