Global Convergence of Gradient EM for Over-Parameterized Gaussian Mixtures

Learning Gaussian Mixture Models (GMMs) is a fundamental problem in machine learning, with the Expectation-Maximization (EM) algorithm and its popular variant gradient EM being arguably the most widely used algorithms in practice. In the exact-parameterized setting, where both the ground truth GMM and the learning model have the same number of components $m$, a vast line of work has aimed to establish rigorous recovery guarantees for EM. However, global convergence has only been proven for the case of $m=2$, and EM is known to fail to recover the ground truth when $m\geq 3$. In this paper, we consider the $\textit{over-parameterized}$ setting, where the learning model uses $n>m$ components to fit an $m$-component ground truth GMM. In contrast to the exact-parameterized case, we provide a rigorous global convergence guarantee for gradient EM. Specifically, for any well separated GMMs in general position, we prove that with only mild over-parameterization $n = \Omega(m\log m)$, randomly initialized gradient EM converges globally to the ground truth at a polynomial rate with polynomial samples. Our analysis proceeds in two stages and introduces a suite of novel tools for Gaussian Mixture analysis. We use Hermite polynomials to study the dynamics of gradient EM and employ tensor decomposition to characterize the geometric landscape of the likelihood loss. This is the first global convergence and recovery result for EM or Gradient EM beyond the special case of $m=2$.

UniRes: Universal Image Restoration for Complex Degradations

Real-world image restoration is hampered by diverse degradations stemming from varying capture conditions, capture devices and post-processing pipelines. Existing works make improvements through simulating those degradations and leveraging image generative priors, however generalization to in-the-wild data remains an unresolved problem. In this paper, we focus on complex degradations, i.e., arbitrary mixtures of multiple types of known degradations, which is frequently seen in the wild. A simple yet flexible diffusionbased framework, named UniRes, is proposed to address such degradations in an end-to-end manner. It combines several specialized models during the diffusion sampling steps, hence transferring the knowledge from several well-isolated restoration tasks to the restoration of complex in-the-wild degradations. This only requires well-isolated training data for several degradation types. The framework is flexible as extensions can be added through a unified formulation, and the fidelity-quality trade-off can be adjusted through a new paradigm. Our proposed method is evaluated on both complex-degradation and single-degradation image restoration datasets. Extensive qualitative and quantitative experimental results show consistent performance gain especially for images with complex degradations.

Reference-Guided Identity Preserving Face Restoration

Preserving face identity is a critical yet persistent challenge in diffusion-based image restoration. While reference faces offer a path forward, existing reference-based methods often fail to fully exploit their potential. This paper introduces a novel approach that maximizes reference face utility for improved face restoration and identity preservation. Our method makes three key contributions: 1) Composite Context, a comprehensive representation that fuses multi-level (high- and low-level) information from the reference face, offering richer guidance than prior singular representations. 2) Hard Example Identity Loss, a novel loss function that leverages the reference face to address the identity learning inefficiencies found in the existing identity loss. 3) A training-free method to adapt the model to multi-reference inputs during inference. The proposed method demonstrably restores high-quality faces and achieves state-of-the-art identity preserving restoration on benchmarks such as FFHQ-Ref and CelebA-Ref-Test, consistently outperforming previous work.

Chordless Structure: A Pathway to Simple and Expressive GNNs

Researchers have proposed various methods of incorporating more structured information into the design of Graph Neural Networks (GNNs) to enhance their expressiveness. However, these methods are either computationally expensive or lacking in provable expressiveness. In this paper, we observe that the chords increase the complexity of the graph structure while contributing little useful information in many cases. In contrast, chordless structures are more efficient and effective for representing the graph. Therefore, when leveraging the information of cycles, we choose to omit the chords. Accordingly, we propose a Chordless Structure-based Graph Neural Network (CSGNN) and prove that its expressiveness is strictly more powerful than the k-hop GNN (KPGNN) with polynomial complexity. Experimental results on real-world datasets demonstrate that CSGNN outperforms existing GNNs across various graph tasks while incurring lower computational costs and achieving better performance than the GNNs of 3-WL expressiveness.

FlashForge: Ultra-Efficient Prefix-Aware Attention for LLM Decoding

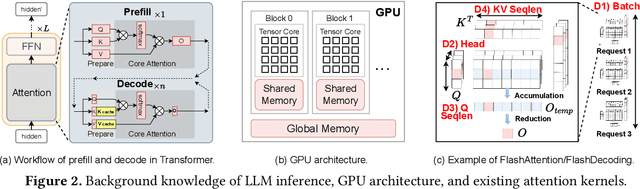
Prefix-sharing among multiple prompts presents opportunities to combine the operations of the shared prefix, while attention computation in the decode stage, which becomes a critical bottleneck with increasing context lengths, is a memory-intensive process requiring heavy memory access on the key-value (KV) cache of the prefixes. Therefore, in this paper, we explore the potential of prefix-sharing in the attention computation of the decode stage. However, the tree structure of the prefix-sharing mechanism presents significant challenges for attention computation in efficiently processing shared KV cache access patterns while managing complex dependencies and balancing irregular workloads. To address the above challenges, we propose a dedicated attention kernel to combine the memory access of shared prefixes in the decoding stage, namely FlashForge. FlashForge delivers two key innovations: a novel shared-prefix attention kernel that optimizes memory hierarchy and exploits both intra-block and inter-block parallelism, and a comprehensive workload balancing mechanism that efficiently estimates cost, divides tasks, and schedules execution. Experimental results show that FlashForge achieves an average 1.9x speedup and 120.9x memory access reduction compared to the state-of-the-art FlashDecoding kernel regarding attention computation in the decode stage and 3.8x end-to-end time per output token compared to the vLLM.

PartStickers: Generating Parts of Objects for Rapid Prototyping

Design prototyping involves creating mockups of products or concepts to gather feedback and iterate on ideas. While prototyping often requires specific parts of objects, such as when constructing a novel creature for a video game, existing text-to-image methods tend to only generate entire objects. To address this, we propose a novel task and method of ``part sticker generation", which entails generating an isolated part of an object on a neutral background. Experiments demonstrate our method outperforms state-of-the-art baselines with respect to realism and text alignment, while preserving object-level generation capabilities. We publicly share our code and models to encourage community-wide progress on this new task: https://partsticker.github.io.

ProbDiffFlow: An Efficient Learning-Free Framework for Probabilistic Single-Image Optical Flow Estimation

This paper studies optical flow estimation, a critical task in motion analysis with applications in autonomous navigation, action recognition, and film production. Traditional optical flow methods require consecutive frames, which are often unavailable due to limitations in data acquisition or real-world scene disruptions. Thus, single-frame optical flow estimation is emerging in the literature. However, existing single-frame approaches suffer from two major limitations: (1) they rely on labeled training data, making them task-specific, and (2) they produce deterministic predictions, failing to capture motion uncertainty. To overcome these challenges, we propose ProbDiffFlow, a training-free framework that estimates optical flow distributions from a single image. Instead of directly predicting motion, ProbDiffFlow follows an estimation-by-synthesis paradigm: it first generates diverse plausible future frames using a diffusion-based model, then estimates motion from these synthesized samples using a pre-trained optical flow model, and finally aggregates the results into a probabilistic flow distribution. This design eliminates the need for task-specific training while capturing multiple plausible motions. Experiments on both synthetic and real-world datasets demonstrate that ProbDiffFlow achieves superior accuracy, diversity, and efficiency, outperforming existing single-image and two-frame baselines.

Gradient-Guided Parameter Mask for Multi-Scenario Image Restoration Under Adverse Weather

Removing adverse weather conditions such as rain, raindrop, and snow from images is critical for various real-world applications, including autonomous driving, surveillance, and remote sensing. However, existing multi-task approaches typically rely on augmenting the model with additional parameters to handle multiple scenarios. While this enables the model to address diverse tasks, the introduction of extra parameters significantly complicates its practical deployment. In this paper, we propose a novel Gradient-Guided Parameter Mask for Multi-Scenario Image Restoration under adverse weather, designed to effectively handle image degradation under diverse weather conditions without additional parameters. Our method segments model parameters into common and specific components by evaluating the gradient variation intensity during training for each specific weather condition. This enables the model to precisely and adaptively learn relevant features for each weather scenario, improving both efficiency and effectiveness without compromising on performance. This method constructs specific masks based on gradient fluctuations to isolate parameters influenced by other tasks, ensuring that the model achieves strong performance across all scenarios without adding extra parameters. We demonstrate the state-of-the-art performance of our framework through extensive experiments on multiple benchmark datasets. Specifically, our method achieves PSNR scores of 29.22 on the Raindrop dataset, 30.76 on the Rain dataset, and 29.56 on the Snow100K dataset. Code is available at: \href{https://github.com/AierLab/MultiTask}{https://github.com/AierLab/MultiTask}.

V2X-Radar: A Multi-modal Dataset with 4D Radar for Cooperative Perception

Modern autonomous vehicle perception systems often struggle with occlusions and limited perception range. Previous studies have demonstrated the effectiveness of cooperative perception in extending the perception range and overcoming occlusions, thereby improving the safety of autonomous driving. In recent years, a series of cooperative perception datasets have emerged. However, these datasets only focus on camera and LiDAR, overlooking 4D Radar, a sensor employed in single-vehicle autonomous driving for robust perception in adverse weather conditions. In this paper, to bridge the gap of missing 4D Radar datasets in cooperative perception, we present V2X-Radar, the first large real-world multi-modal dataset featuring 4D Radar. Our V2X-Radar dataset is collected using a connected vehicle platform and an intelligent roadside unit equipped with 4D Radar, LiDAR, and multi-view cameras. The collected data includes sunny and rainy weather conditions, spanning daytime, dusk, and nighttime, as well as typical challenging scenarios. The dataset comprises 20K LiDAR frames, 40K camera images, and 20K 4D Radar data, with 350K annotated bounding boxes across five categories. To facilitate diverse research domains, we establish V2X-Radar-C for cooperative perception, V2X-Radar-I for roadside perception, and V2X-Radar-V for single-vehicle perception. We further provide comprehensive benchmarks of recent perception algorithms on the above three sub-datasets. The dataset and benchmark codebase will be available at \url{http://openmpd.com/column/V2X-Radar}.

Score-based Neural Ordinary Differential Equations for Computing Mean Field Control Problems

Classical neural ordinary differential equations (ODEs) are powerful tools for approximating the log-density functions in high-dimensional spaces along trajectories, where neural networks parameterize the velocity fields. This paper proposes a system of neural differential equations representing first- and second-order score functions along trajectories based on deep neural networks. We reformulate the mean field control (MFC) problem with individual noises into an unconstrained optimization problem framed by the proposed neural ODE system. Additionally, we introduce a novel regularization term to enforce characteristics of viscous Hamilton--Jacobi--Bellman (HJB) equations to be satisfied based on the evolution of the second-order score function. Examples include regularized Wasserstein proximal operators (RWPOs), probability flow matching of Fokker--Planck (FP) equations, and linear quadratic (LQ) MFC problems, which demonstrate the effectiveness and accuracy of the proposed method.