Transformers Trained via Gradient Descent Can Provably Learn a Class of Teacher Models

Transformers have achieved great success across a wide range of applications, yet the theoretical foundations underlying their success remain largely unexplored. To demystify the strong capacities of transformers applied to versatile scenarios and tasks, we theoretically investigate utilizing transformers as students to learn from a class of teacher models. Specifically, the teacher models covered in our analysis include convolution layers with average pooling, graph convolution layers, and various classic statistical learning models, including a variant of sparse token selection models [Sanford et al., 2023, Wang et al., 2024] and group-sparse linear predictors [Zhang et al., 2025]. When learning from this class of teacher models, we prove that one-layer transformers with simplified "position-only'' attention can successfully recover all parameter blocks of the teacher models, thus achieving the optimal population loss. Building upon the efficient mimicry of trained transformers towards teacher models, we further demonstrate that they can generalize well to a broad class of out-of-distribution data under mild assumptions. The key in our analysis is to identify a fundamental bilinear structure shared by various learning tasks, which enables us to establish unified learning guarantees for these tasks when treating them as teachers for transformers.

Dimension-Independent Convergence of Underdamped Langevin Monte Carlo in KL Divergence

Underdamped Langevin dynamics (ULD) is a widely-used sampler for Gibbs distributions $π\propto e^{-V}$, and is often empirically effective in high dimensions. However, existing non-asymptotic convergence guarantees for discretized ULD typically scale polynomially with the ambient dimension $d$, leading to vacuous bounds when $d$ is large. The main known dimension-free result concerns the randomized midpoint discretization in Wasserstein-2 distance (Liu et al.,2023), while dimension-independent guarantees for ULD discretizations in KL divergence have remained open. We close this gap by proving the first dimension-free KL divergence bounds for discretized ULD. Our analysis refines the KL local error framework (Altschuler et al., 2025) to a dimension-free setting and yields bounds that depend on $\mathrm{tr}(\mathbf{H})$, where $\mathbf{H}$ upper bounds the Hessian of $V$, rather than on $d$. As a consequence, we obtain improved iteration complexity for underdamped Langevin Monte Carlo relative to overdamped Langevin methods in regimes where $\mathrm{tr}(\mathbf{H})\ll d$.

Near-Optimal Regret for KL-Regularized Multi-Armed Bandits

Recent studies have shown that reinforcement learning with KL-regularized objectives can enjoy faster rates of convergence or logarithmic regret, in contrast to the classical $\sqrt{T}$-type regret in the unregularized setting. However, the statistical efficiency of online learning with respect to KL-regularized objectives remains far from completely characterized, even when specialized to multi-armed bandits (MABs). We address this problem for MABs via a sharp analysis of KL-UCB using a novel peeling argument, which yields a $\tilde{O}(ηK\log^2T)$ upper bound: the first high-probability regret bound with linear dependence on $K$. Here, $T$ is the time horizon, $K$ is the number of arms, $η^{-1}$ is the regularization intensity, and $\tilde{O}$ hides all logarithmic factors except those involving $\log T$. The near-tightness of our analysis is certified by the first non-constant lower bound $Ω(ηK \log T)$, which follows from subtle hard-instance constructions and a tailored decomposition of the Bayes prior. Moreover, in the low-regularization regime (i.e., large $η$), we show that the KL-regularized regret for MABs is $η$-independent and scales as $\tildeΘ(\sqrt{KT})$. Overall, our results provide a thorough understanding of KL-regularized MABs across all regimes of $η$ and yield nearly optimal bounds in terms of $K$, $η$, and $T$.

Protein Autoregressive Modeling via Multiscale Structure Generation

We present protein autoregressive modeling (PAR), the first multi-scale autoregressive framework for protein backbone generation via coarse-to-fine next-scale prediction. Using the hierarchical nature of proteins, PAR generates structures that mimic sculpting a statue, forming a coarse topology and refining structural details over scales. To achieve this, PAR consists of three key components: (i) multi-scale downsampling operations that represent protein structures across multiple scales during training; (ii) an autoregressive transformer that encodes multi-scale information and produces conditional embeddings to guide structure generation; (iii) a flow-based backbone decoder that generates backbone atoms conditioned on these embeddings. Moreover, autoregressive models suffer from exposure bias, caused by the training and the generation procedure mismatch, and substantially degrades structure generation quality. We effectively alleviate this issue by adopting noisy context learning and scheduled sampling, enabling robust backbone generation. Notably, PAR exhibits strong zero-shot generalization, supporting flexible human-prompted conditional generation and motif scaffolding without requiring fine-tuning. On the unconditional generation benchmark, PAR effectively learns protein distributions and produces backbones of high design quality, and exhibits favorable scaling behavior. Together, these properties establish PAR as a promising framework for protein structure generation.

Scalable Spatio-Temporal SE(3) Diffusion for Long-Horizon Protein Dynamics

Molecular dynamics (MD) simulations remain the gold standard for studying protein dynamics, but their computational cost limits access to biologically relevant timescales. Recent generative models have shown promise in accelerating simulations, yet they struggle with long-horizon generation due to architectural constraints, error accumulation, and inadequate modeling of spatio-temporal dynamics. We present STAR-MD (Spatio-Temporal Autoregressive Rollout for Molecular Dynamics), a scalable SE(3)-equivariant diffusion model that generates physically plausible protein trajectories over microsecond timescales. Our key innovation is a causal diffusion transformer with joint spatio-temporal attention that efficiently captures complex space-time dependencies while avoiding the memory bottlenecks of existing methods. On the standard ATLAS benchmark, STAR-MD achieves state-of-the-art performance across all metrics--substantially improving conformational coverage, structural validity, and dynamic fidelity compared to previous methods. STAR-MD successfully extrapolates to generate stable microsecond-scale trajectories where baseline methods fail catastrophically, maintaining high structural quality throughout the extended rollout. Our comprehensive evaluation reveals severe limitations in current models for long-horizon generation, while demonstrating that STAR-MD's joint spatio-temporal modeling enables robust dynamics simulation at biologically relevant timescales, paving the way for accelerated exploration of protein function.

Deep Delta Learning

The efficacy of deep residual networks is fundamentally predicated on the identity shortcut connection. While this mechanism effectively mitigates the vanishing gradient problem, it imposes a strictly additive inductive bias on feature transformations, thereby limiting the network's capacity to model complex state transitions. In this paper, we introduce Deep Delta Learning (DDL), a novel architecture that generalizes the standard residual connection by modulating the identity shortcut with a learnable, data-dependent geometric transformation. This transformation, termed the Delta Operator, constitutes a rank-1 perturbation of the identity matrix, parameterized by a reflection direction vector $\mathbf{k}(\mathbf{X})$ and a gating scalar $β(\mathbf{X})$. We provide a spectral analysis of this operator, demonstrating that the gate $β(\mathbf{X})$ enables dynamic interpolation between identity mapping, orthogonal projection, and geometric reflection. Furthermore, we restructure the residual update as a synchronous rank-1 injection, where the gate acts as a dynamic step size governing both the erasure of old information and the writing of new features. This unification empowers the network to explicitly control the spectrum of its layer-wise transition operator, enabling the modeling of complex, non-monotonic dynamics while preserving the stable training characteristics of gated residual architectures.

Group Representational Position Encoding

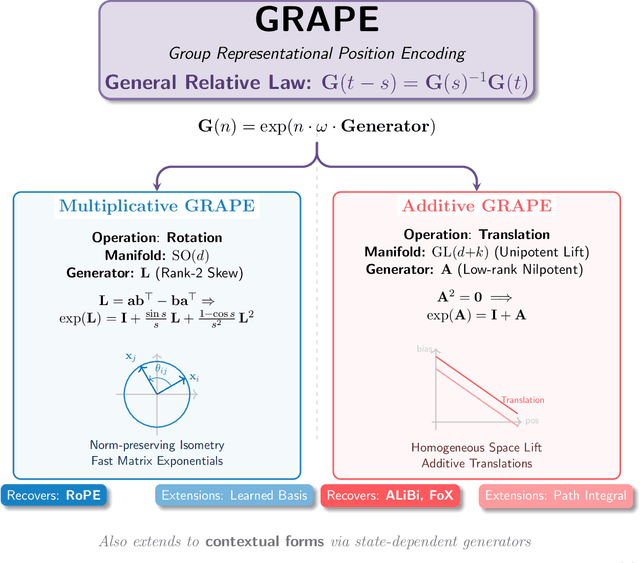
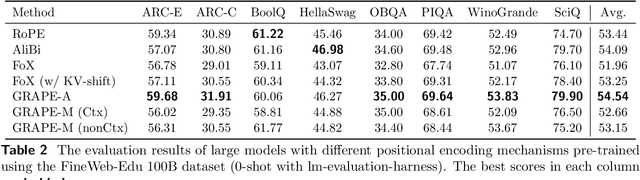
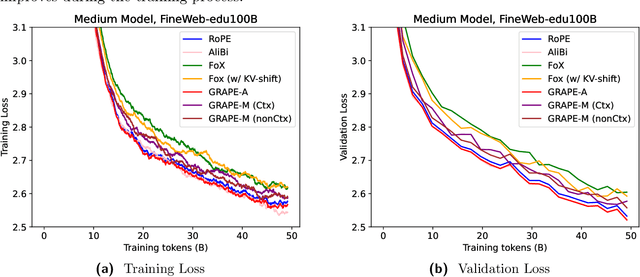
We present GRAPE (Group RepresentAtional Position Encoding), a unified framework for positional encoding based on group actions. GRAPE brings together two families of mechanisms: (i) multiplicative rotations (Multiplicative GRAPE) in $\mathrm{SO}(d)$ and (ii) additive logit biases (Additive GRAPE) arising from unipotent actions in the general linear group $\mathrm{GL}$. In Multiplicative GRAPE, a position $n \in \mathbb{Z}$ (or $t \in \mathbb{R}$) acts as $\mathbf{G}(n)=\exp(n\,ω\,\mathbf{L})$ with a rank-2 skew generator $\mathbf{L} \in \mathbb{R}^{d \times d}$, yielding a relative, compositional, norm-preserving map with a closed-form matrix exponential. RoPE is recovered exactly when the $d/2$ planes are the canonical coordinate pairs with log-uniform spectrum. Learned commuting subspaces and compact non-commuting mixtures strictly extend this geometry to capture cross-subspace feature coupling at $O(d)$ and $O(r d)$ cost per head, respectively. In Additive GRAPE, additive logits arise as rank-1 (or low-rank) unipotent actions, recovering ALiBi and the Forgetting Transformer (FoX) as exact special cases while preserving an exact relative law and streaming cacheability. Altogether, GRAPE supplies a principled design space for positional geometry in long-context models, subsuming RoPE and ALiBi as special cases. Project Page: https://github.com/model-architectures/GRAPE.

Higher-order Linear Attention

The quadratic cost of scaled dot-product attention is a central obstacle to scaling autoregressive language models to long contexts. Linear-time attention and State Space Models (SSMs) provide scalable alternatives but are typically restricted to first-order or kernel-based approximations, which can limit expressivity. We introduce Higher-order Linear Attention (HLA), a causal, streaming mechanism that realizes higher interactions via compact prefix sufficient statistics. In the second-order case, HLA maintains a constant-size state and computes per-token outputs in linear time without materializing any $n \times n$ matrices. We give closed-form streaming identities, a strictly causal masked variant using two additional summaries, and a chunk-parallel training scheme based on associative scans that reproduces the activations of a serial recurrence exactly. We further outline extensions to third and higher orders. Collectively, these results position HLA as a principled, scalable building block that combines attention-like, data-dependent mixing with the efficiency of modern recurrent architectures. Project Page: https://github.com/yifanzhang-pro/HLA.

Causal Attention with Lookahead Keys

In standard causal attention, each token's query, key, and value (QKV) are static and encode only preceding context. We introduce CAuSal aTtention with Lookahead kEys (CASTLE), an attention mechanism that continually updates each token's keys as the context unfolds. We term these updated keys lookahead keys because they belong to earlier positions yet integrate information from tokens that appear later relative to those positions, while strictly preserving the autoregressive property. Although the mechanism appears sequential, we derive a mathematical equivalence that avoids explicitly materializing lookahead keys at each position and enables efficient parallel training. On language modeling benchmarks, CASTLE consistently outperforms standard causal attention across model scales, reducing validation perplexity and improving performance on a range of downstream tasks.

SwingArena: Competitive Programming Arena for Long-context GitHub Issue Solving

We present SwingArena, a competitive evaluation framework for Large Language Models (LLMs) that closely mirrors real-world software development workflows. Unlike traditional static benchmarks, SwingArena models the collaborative process of software iteration by pairing LLMs as submitters, who generate patches, and reviewers, who create test cases and verify the patches through continuous integration (CI) pipelines. To support these interactive evaluations, we introduce a retrieval-augmented code generation (RACG) module that efficiently handles long-context challenges by providing syntactically and semantically relevant code snippets from large codebases, supporting multiple programming languages (C++, Python, Rust, and Go). This enables the framework to scale across diverse tasks and contexts while respecting token limitations. Our experiments, using over 400 high-quality real-world GitHub issues selected from a pool of 2,300 issues, show that models like GPT-4o excel at aggressive patch generation, whereas DeepSeek and Gemini prioritize correctness in CI validation. SwingArena presents a scalable and extensible methodology for evaluating LLMs in realistic, CI-driven software development settings. More details are available on our project page: swing-bench.github.io