A Spectral Condition for Feature Learning

The push to train ever larger neural networks has motivated the study of initialization and training at large network width. A key challenge is to scale training so that a network's internal representations evolve nontrivially at all widths, a process known as feature learning. Here, we show that feature learning is achieved by scaling the spectral norm of weight matrices and their updates like $\sqrt{\texttt{fan-out}/\texttt{fan-in}}$, in contrast to widely used but heuristic scalings based on Frobenius norm and entry size. Our spectral scaling analysis also leads to an elementary derivation of \emph{maximal update parametrization}. All in all, we aim to provide the reader with a solid conceptual understanding of feature learning in neural networks.

Tensor Programs VI: Feature Learning in Infinite-Depth Neural Networks

By classifying infinite-width neural networks and identifying the *optimal* limit, Tensor Programs IV and V demonstrated a universal way, called $\mu$P, for *widthwise hyperparameter transfer*, i.e., predicting optimal hyperparameters of wide neural networks from narrow ones. Here we investigate the analogous classification for *depthwise parametrizations* of deep residual networks (resnets). We classify depthwise parametrizations of block multiplier and learning rate by their infinite-width-then-depth limits. In resnets where each block has only one layer, we identify a unique optimal parametrization, called Depth-$\mu$P that extends $\mu$P and show empirically it admits depthwise hyperparameter transfer. We identify *feature diversity* as a crucial factor in deep networks, and Depth-$\mu$P can be characterized as maximizing both feature learning and feature diversity. Exploiting this, we find that absolute value, among all homogeneous nonlinearities, maximizes feature diversity and indeed empirically leads to significantly better performance. However, if each block is deeper (such as modern transformers), then we find fundamental limitations in all possible infinite-depth limits of such parametrizations, which we illustrate both theoretically and empirically on simple networks as well as Megatron transformer trained on Common Crawl.

Tensor Programs IVb: Adaptive Optimization in the Infinite-Width Limit

Going beyond stochastic gradient descent (SGD), what new phenomena emerge in wide neural networks trained by adaptive optimizers like Adam? Here we show: The same dichotomy between feature learning and kernel behaviors (as in SGD) holds for general optimizers as well, including Adam -- albeit with a nonlinear notion of "kernel." We derive the corresponding "neural tangent" and "maximal update" limits for any architecture. Two foundational advances underlie the above results: 1) A new Tensor Program language, NEXORT, that can express how adaptive optimizers process gradients into updates. 2) The introduction of bra-ket notation to drastically simplify expressions and calculations in Tensor Programs. This work summarizes and generalizes all previous results in the Tensor Programs series of papers.

Width and Depth Limits Commute in Residual Networks

We show that taking the width and depth to infinity in a deep neural network with skip connections, when branches are scaled by $1/\sqrt{depth}$ (the only nontrivial scaling), result in the same covariance structure no matter how that limit is taken. This explains why the standard infinite-width-then-depth approach provides practical insights even for networks with depth of the same order as width. We also demonstrate that the pre-activations, in this case, have Gaussian distributions which has direct applications in Bayesian deep learning. We conduct extensive simulations that show an excellent match with our theoretical findings.

High-dimensional Asymptotics of Feature Learning: How One Gradient Step Improves the Representation

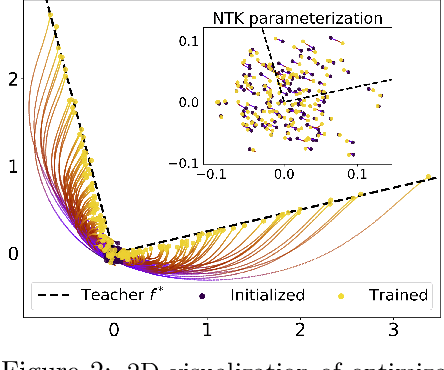
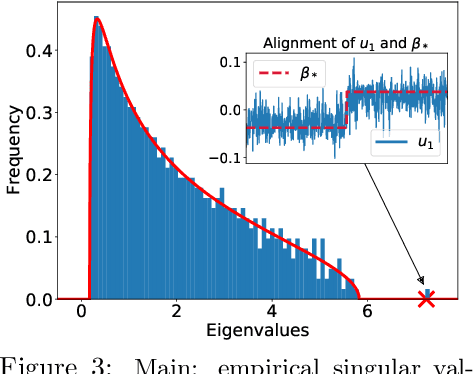
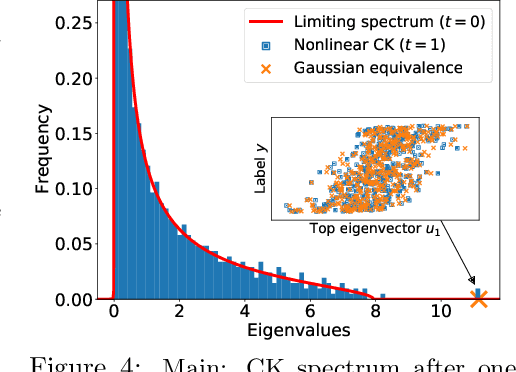
We study the first gradient descent step on the first-layer parameters $\boldsymbol{W}$ in a two-layer neural network: $f(\boldsymbol{x}) = \frac{1}{\sqrt{N}}\boldsymbol{a}^\top\sigma(\boldsymbol{W}^\top\boldsymbol{x})$, where $\boldsymbol{W}\in\mathbb{R}^{d\times N}, \boldsymbol{a}\in\mathbb{R}^{N}$ are randomly initialized, and the training objective is the empirical MSE loss: $\frac{1}{n}\sum_{i=1}^n (f(\boldsymbol{x}_i)-y_i)^2$. In the proportional asymptotic limit where $n,d,N\to\infty$ at the same rate, and an idealized student-teacher setting, we show that the first gradient update contains a rank-1 "spike", which results in an alignment between the first-layer weights and the linear component of the teacher model $f^*$. To characterize the impact of this alignment, we compute the prediction risk of ridge regression on the conjugate kernel after one gradient step on $\boldsymbol{W}$ with learning rate $\eta$, when $f^*$ is a single-index model. We consider two scalings of the first step learning rate $\eta$. For small $\eta$, we establish a Gaussian equivalence property for the trained feature map, and prove that the learned kernel improves upon the initial random features model, but cannot defeat the best linear model on the input. Whereas for sufficiently large $\eta$, we prove that for certain $f^*$, the same ridge estimator on trained features can go beyond this "linear regime" and outperform a wide range of random features and rotationally invariant kernels. Our results demonstrate that even one gradient step can lead to a considerable advantage over random features, and highlight the role of learning rate scaling in the initial phase of training.

Tensor Programs V: Tuning Large Neural Networks via Zero-Shot Hyperparameter Transfer

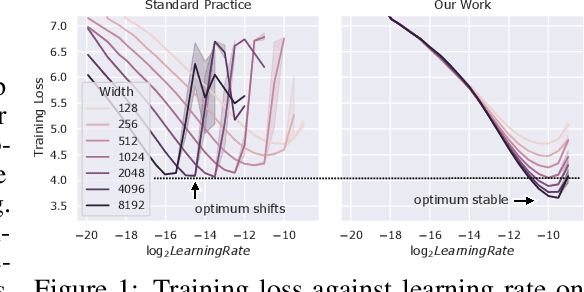
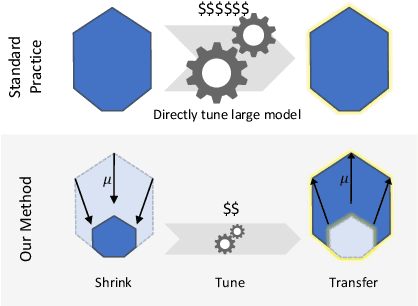
Hyperparameter (HP) tuning in deep learning is an expensive process, prohibitively so for neural networks (NNs) with billions of parameters. We show that, in the recently discovered Maximal Update Parametrization (muP), many optimal HPs remain stable even as model size changes. This leads to a new HP tuning paradigm we call muTransfer: parametrize the target model in muP, tune the HP indirectly on a smaller model, and zero-shot transfer them to the full-sized model, i.e., without directly tuning the latter at all. We verify muTransfer on Transformer and ResNet. For example, 1) by transferring pretraining HPs from a model of 13M parameters, we outperform published numbers of BERT-large (350M parameters), with a total tuning cost equivalent to pretraining BERT-large once; 2) by transferring from 40M parameters, we outperform published numbers of the 6.7B GPT-3 model, with tuning cost only 7% of total pretraining cost. A Pytorch implementation of our technique can be found at github.com/microsoft/mup and installable via `pip install mup`.

CLUES: Few-Shot Learning Evaluation in Natural Language Understanding

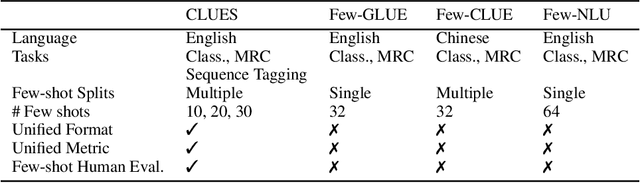
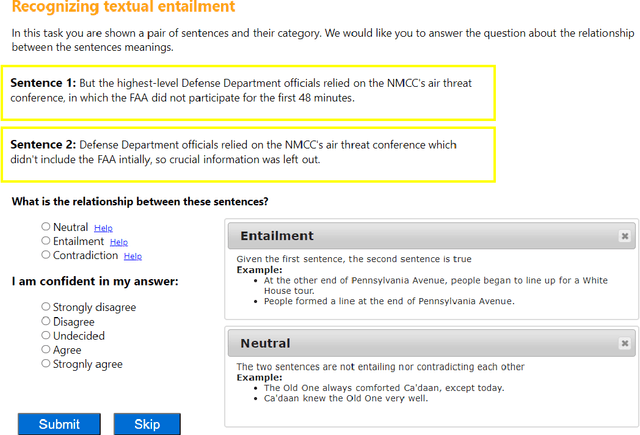
Most recent progress in natural language understanding (NLU) has been driven, in part, by benchmarks such as GLUE, SuperGLUE, SQuAD, etc. In fact, many NLU models have now matched or exceeded "human-level" performance on many tasks in these benchmarks. Most of these benchmarks, however, give models access to relatively large amounts of labeled data for training. As such, the models are provided far more data than required by humans to achieve strong performance. That has motivated a line of work that focuses on improving few-shot learning performance of NLU models. However, there is a lack of standardized evaluation benchmarks for few-shot NLU resulting in different experimental settings in different papers. To help accelerate this line of work, we introduce CLUES (Constrained Language Understanding Evaluation Standard), a benchmark for evaluating the few-shot learning capabilities of NLU models. We demonstrate that while recent models reach human performance when they have access to large amounts of labeled data, there is a huge gap in performance in the few-shot setting for most tasks. We also demonstrate differences between alternative model families and adaptation techniques in the few shot setting. Finally, we discuss several principles and choices in designing the experimental settings for evaluating the true few-shot learning performance and suggest a unified standardized approach to few-shot learning evaluation. We aim to encourage research on NLU models that can generalize to new tasks with a small number of examples. Code and data for CLUES are available at https://github.com/microsoft/CLUES.

Implicit Acceleration and Feature Learning in Infinitely Wide Neural Networks with Bottlenecks

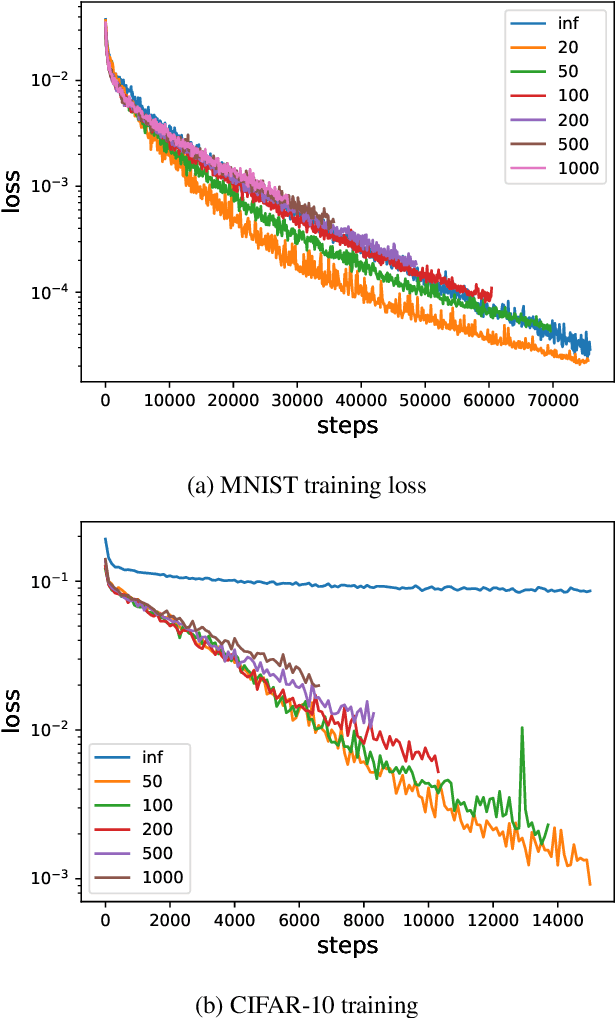
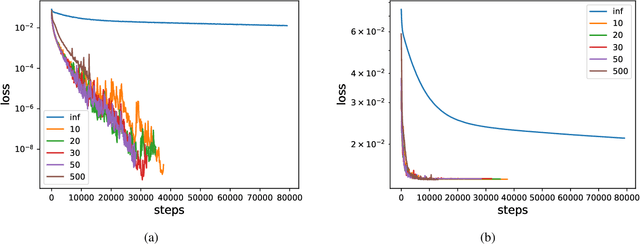
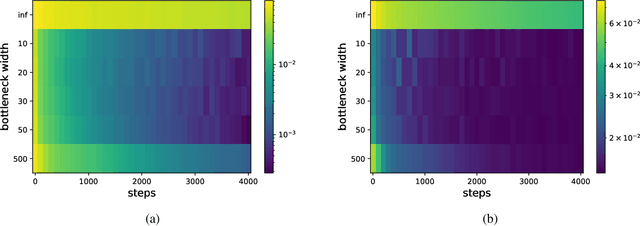
We analyze the learning dynamics of infinitely wide neural networks with a finite sized bottle-neck. Unlike the neural tangent kernel limit, a bottleneck in an otherwise infinite width network al-lows data dependent feature learning in its bottle-neck representation. We empirically show that a single bottleneck in infinite networks dramatically accelerates training when compared to purely in-finite networks, with an improved overall performance. We discuss the acceleration phenomena by drawing similarities to infinitely wide deep linear models, where the acceleration effect of a bottleneck can be understood theoretically.

3DB: A Framework for Debugging Computer Vision Models

We introduce 3DB: an extendable, unified framework for testing and debugging vision models using photorealistic simulation. We demonstrate, through a wide range of use cases, that 3DB allows users to discover vulnerabilities in computer vision systems and gain insights into how models make decisions. 3DB captures and generalizes many robustness analyses from prior work, and enables one to study their interplay. Finally, we find that the insights generated by the system transfer to the physical world. We are releasing 3DB as a library (https://github.com/3db/3db) alongside a set of example analyses, guides, and documentation: https://3db.github.io/3db/ .

Tensor Programs IIb: Architectural Universality of Neural Tangent Kernel Training Dynamics

Yang (2020a) recently showed that the Neural Tangent Kernel (NTK) at initialization has an infinite-width limit for a large class of architectures including modern staples such as ResNet and Transformers. However, their analysis does not apply to training. Here, we show the same neural networks (in the so-called NTK parametrization) during training follow a kernel gradient descent dynamics in function space, where the kernel is the infinite-width NTK. This completes the proof of the *architectural universality* of NTK behavior. To achieve this result, we apply the Tensor Programs technique: Write the entire SGD dynamics inside a Tensor Program and analyze it via the Master Theorem. To facilitate this proof, we develop a graphical notation for Tensor Programs.