Time Series Analysis
Time series analysis comprises statistical methods for analyzing a sequence of data points collected over an interval of time to identify interesting patterns and trends.
Papers and Code
Eco-Friendly AI: Unleashing Data Power for Green Federated Learning
Jul 23, 2025The widespread adoption of Artificial Intelligence (AI) and Machine Learning (ML) comes with a significant environmental impact, particularly in terms of energy consumption and carbon emissions. This pressing issue highlights the need for innovative solutions to mitigate AI's ecological footprint. One of the key factors influencing the energy consumption of ML model training is the size of the training dataset. ML models are often trained on vast amounts of data continuously generated by sensors and devices distributed across multiple locations. To reduce data transmission costs and enhance privacy, Federated Learning (FL) enables model training without the need to move or share raw data. While FL offers these advantages, it also introduces challenges due to the heterogeneity of data sources (related to volume and quality), computational node capabilities, and environmental impact. This paper contributes to the advancement of Green AI by proposing a data-centric approach to Green Federated Learning. Specifically, we focus on reducing FL's environmental impact by minimizing the volume of training data. Our methodology involves the analysis of the characteristics of federated datasets, the selecting of an optimal subset of data based on quality metrics, and the choice of the federated nodes with the lowest environmental impact. We develop a comprehensive methodology that examines the influence of data-centric factors, such as data quality and volume, on FL training performance and carbon emissions. Building on these insights, we introduce an interactive recommendation system that optimizes FL configurations through data reduction, minimizing environmental impact during training. Applying this methodology to time series classification has demonstrated promising results in reducing the environmental impact of FL tasks.
A Novel Modeling Framework and Data Product for Extended VIIRS-like Artificial Nighttime Light Image Reconstruction (1986-2024)
Aug 01, 2025
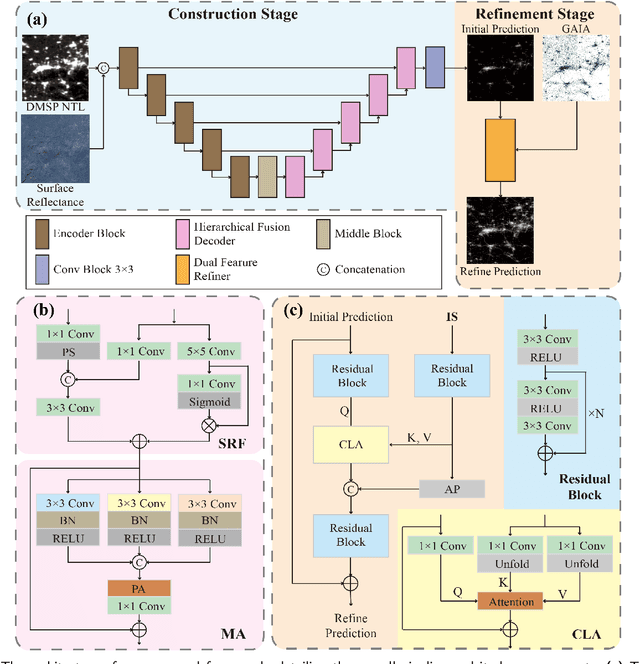
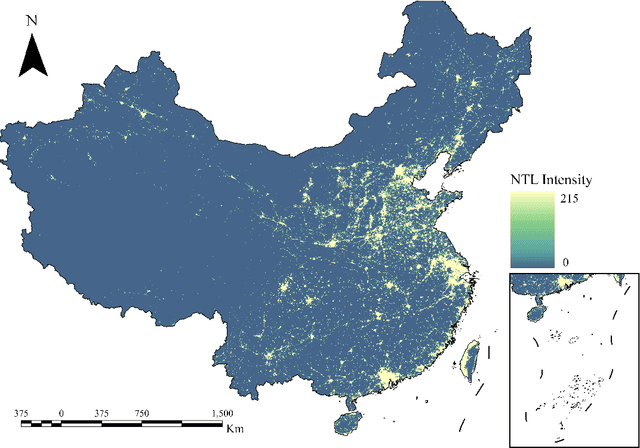
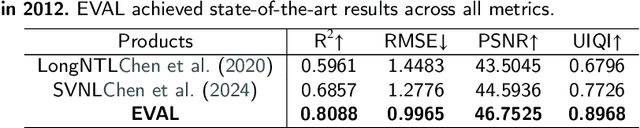
Artificial Night-Time Light (NTL) remote sensing is a vital proxy for quantifying the intensity and spatial distribution of human activities. Although the NPP-VIIRS sensor provides high-quality NTL observations, its temporal coverage, which begins in 2012, restricts long-term time-series studies that extend to earlier periods. Despite the progress in extending VIIRS-like NTL time-series, current methods still suffer from two significant shortcomings: the underestimation of light intensity and the structural omission. To overcome these limitations, we propose a novel reconstruction framework consisting of a two-stage process: construction and refinement. The construction stage features a Hierarchical Fusion Decoder (HFD) designed to enhance the fidelity of the initial reconstruction. The refinement stage employs a Dual Feature Refiner (DFR), which leverages high-resolution impervious surface masks to guide and enhance fine-grained structural details. Based on this framework, we developed the Extended VIIRS-like Artificial Nighttime Light (EVAL) product for China, extending the standard data record backwards by 26 years to begin in 1986. Quantitative evaluation shows that EVAL significantly outperforms existing state-of-the-art products, boosting the $\text{R}^2$ from 0.68 to 0.80 while lowering the RMSE from 1.27 to 0.99. Furthermore, EVAL exhibits excellent temporal consistency and maintains a high correlation with socioeconomic parameters, confirming its reliability for long-term analysis. The resulting EVAL dataset provides a valuable new resource for the research community and is publicly available at https://doi.org/10.11888/HumanNat.tpdc.302930.
Multiresolution local smoothness detection in non-uniformly sampled multivariate signals
Jul 17, 2025Inspired by edge detection based on the decay behavior of wavelet coefficients, we introduce a (near) linear-time algorithm for detecting the local regularity in non-uniformly sampled multivariate signals. Our approach quantifies regularity within the framework of microlocal spaces introduced by Jaffard. The central tool in our analysis is the fast samplet transform, a distributional wavelet transform tailored to scattered data. We establish a connection between the decay of samplet coefficients and the pointwise regularity of multivariate signals. As a by product, we derive decay estimates for functions belonging to classical H\"older spaces and Sobolev-Slobodeckij spaces. While traditional wavelets are effective for regularity detection in low-dimensional structured data, samplets demonstrate robust performance even for higher dimensional and scattered data. To illustrate our theoretical findings, we present extensive numerical studies detecting local regularity of one-, two- and three-dimensional signals, ranging from non-uniformly sampled time series over image segmentation to edge detection in point clouds.
A Practical Analysis: Understanding Phase Noise Modelling in Time and Frequency Domain for Phase-Locked Loops
Jul 16, 2025In MIMO systems, the presence of phase noise is a significant factor that can degrade performance. For MIMO testbeds build from SDR devices, phase noise cannot be ignored, particular in applications that require phase synchronization. This is especially relevant in MIMO systems that employ digital beamforming, where precise phase alignment is crucial. Accordingly, accurate phase noise modelling of SDR devices is essential. However, the information provided in data sheets for different SDR models varies widely and is often insufficient for comprehensive characterization of their phase noise performance. While numerical simulations of PLL phase noise behavior are documented in the literature, there is a lack of extensive measurements supported by appropriate system modelling. In this work, we present a practical phase noise modeling methodology applied to an SDR from the USRP X310 series. Based on measurement data, we derive estimates of key PLL performance indicators such as cycle-to-cycle jitter, oscillator constants, and PLL bandwidth. Furthermore, we propose a parametric model for the phase noise PSD of the PLL circuit and provide corresponding parameter estimates. This model can be used for further investigation into the impact of phase noise on MIMO system performance implemented by similar SDR devices.
Tailored Architectures for Time Series Forecasting: Evaluating Deep Learning Models on Gaussian Process-Generated Data
Jun 10, 2025Developments in Deep Learning have significantly improved time series forecasting by enabling more accurate modeling of complex temporal dependencies inherent in sequential data. The effectiveness of such models is often demonstrated on limited sets of specific real-world data. Although this allows for comparative analysis, it still does not demonstrate how specific data characteristics align with the architectural strengths of individual models. Our research aims at uncovering clear connections between time series characteristics and particular models. We introduce a novel dataset generated using Gaussian Processes, specifically designed to display distinct, known characteristics for targeted evaluations of model adaptability to them. Furthermore, we present TimeFlex, a new model that incorporates a modular architecture tailored to handle diverse temporal dynamics, including trends and periodic patterns. This model is compared to current state-of-the-art models, offering a deeper understanding of how models perform under varied time series conditions.
Anomaly Detection and Generation with Diffusion Models: A Survey
Jun 11, 2025



Anomaly detection (AD) plays a pivotal role across diverse domains, including cybersecurity, finance, healthcare, and industrial manufacturing, by identifying unexpected patterns that deviate from established norms in real-world data. Recent advancements in deep learning, specifically diffusion models (DMs), have sparked significant interest due to their ability to learn complex data distributions and generate high-fidelity samples, offering a robust framework for unsupervised AD. In this survey, we comprehensively review anomaly detection and generation with diffusion models (ADGDM), presenting a tutorial-style analysis of the theoretical foundations and practical implementations and spanning images, videos, time series, tabular, and multimodal data. Crucially, unlike existing surveys that often treat anomaly detection and generation as separate problems, we highlight their inherent synergistic relationship. We reveal how DMs enable a reinforcing cycle where generation techniques directly address the fundamental challenge of anomaly data scarcity, while detection methods provide critical feedback to improve generation fidelity and relevance, advancing both capabilities beyond their individual potential. A detailed taxonomy categorizes ADGDM methods based on anomaly scoring mechanisms, conditioning strategies, and architectural designs, analyzing their strengths and limitations. We final discuss key challenges including scalability and computational efficiency, and outline promising future directions such as efficient architectures, conditioning strategies, and integration with foundation models (e.g., visual-language models and large language models). By synthesizing recent advances and outlining open research questions, this survey aims to guide researchers and practitioners in leveraging DMs for innovative AD solutions across diverse applications.
Why Do Class-Dependent Evaluation Effects Occur with Time Series Feature Attributions? A Synthetic Data Investigation
Jun 13, 2025Evaluating feature attribution methods represents a critical challenge in explainable AI (XAI), as researchers typically rely on perturbation-based metrics when ground truth is unavailable. However, recent work demonstrates that these evaluation metrics can show different performance across predicted classes within the same dataset. These "class-dependent evaluation effects" raise questions about whether perturbation analysis reliably measures attribution quality, with direct implications for XAI method development and the trustworthiness of evaluation techniques. We investigate under which conditions these class-dependent effects arise by conducting controlled experiments with synthetic time series data where ground truth feature locations are known. We systematically vary feature types and class contrasts across binary classification tasks, then compare perturbation-based degradation scores with ground truth-based precision-recall metrics using multiple attribution methods. Our experiments demonstrate that class-dependent effects emerge with both evaluation approaches even in simple scenarios with temporally localized features, triggered by basic variations in feature amplitude or temporal extent between classes. Most critically, we find that perturbation-based and ground truth metrics frequently yield contradictory assessments of attribution quality across classes, with weak correlations between evaluation approaches. These findings suggest that researchers should interpret perturbation-based metrics with care, as they may not always align with whether attributions correctly identify discriminating features. These findings reveal opportunities to reconsider what attribution evaluation actually measures and to develop more comprehensive evaluation frameworks that capture multiple dimensions of attribution quality.
AI-Based Demand Forecasting and Load Balancing for Optimising Energy use in Healthcare Systems: A real case study
Jul 08, 2025This paper tackles the urgent need for efficient energy management in healthcare facilities, where fluctuating demands challenge operational efficiency and sustainability. Traditional methods often prove inadequate, causing inefficiencies and higher costs. To address this, the study presents an AI-based framework combining Long Short-Term Memory (LSTM), genetic algorithm (GA), and SHAP (Shapley Additive Explanations), specifically designed for healthcare energy management. Although LSTM is widely used for time-series forecasting, its application in healthcare energy prediction remains underexplored. The results reveal that LSTM significantly outperforms ARIMA and Prophet models in forecasting complex, non-linear demand patterns. LSTM achieves a Mean Absolute Error (MAE) of 21.69 and Root Mean Square Error (RMSE) of 29.96, far better than Prophet (MAE: 59.78, RMSE: 81.22) and ARIMA (MAE: 87.73, RMSE: 125.22), demonstrating superior performance. The genetic algorithm is applied to optimize model parameters and improve load balancing strategies, enabling adaptive responses to real-time energy fluctuations. SHAP analysis further enhances model transparency by explaining the influence of different features on predictions, fostering trust in decision-making processes. This integrated LSTM-GA-SHAP approach offers a robust solution for improving forecasting accuracy, boosting energy efficiency, and advancing sustainability in healthcare facilities. Future research may explore real-time deployment and hybridization with reinforcement learning for continuous optimization. Overall, the study establishes a solid foundation for using AI in healthcare energy management, highlighting its scalability, efficiency, and resilience potential.
TIMING: Temporality-Aware Integrated Gradients for Time Series Explanation
Jun 05, 2025Recent explainable artificial intelligence (XAI) methods for time series primarily estimate point-wise attribution magnitudes, while overlooking the directional impact on predictions, leading to suboptimal identification of significant points. Our analysis shows that conventional Integrated Gradients (IG) effectively capture critical points with both positive and negative impacts on predictions. However, current evaluation metrics fail to assess this capability, as they inadvertently cancel out opposing feature contributions. To address this limitation, we propose novel evaluation metrics-Cumulative Prediction Difference (CPD) and Cumulative Prediction Preservation (CPP)-to systematically assess whether attribution methods accurately identify significant positive and negative points in time series XAI. Under these metrics, conventional IG outperforms recent counterparts. However, directly applying IG to time series data may lead to suboptimal outcomes, as generated paths ignore temporal relationships and introduce out-of-distribution samples. To overcome these challenges, we introduce TIMING, which enhances IG by incorporating temporal awareness while maintaining its theoretical properties. Extensive experiments on synthetic and real-world time series benchmarks demonstrate that TIMING outperforms existing time series XAI baselines. Our code is available at https://github.com/drumpt/TIMING.
A Kernel-Based Approach for Accurate Steady-State Detection in Performance Time Series
Jun 04, 2025This paper addresses the challenge of accurately detecting the transition from the warmup phase to the steady state in performance metric time series, which is a critical step for effective benchmarking. The goal is to introduce a method that avoids premature or delayed detection, which can lead to inaccurate or inefficient performance analysis. The proposed approach adapts techniques from the chemical reactors domain, detecting steady states online through the combination of kernel-based step detection and statistical methods. By using a window-based approach, it provides detailed information and improves the accuracy of identifying phase transitions, even in noisy or irregular time series. Results show that the new approach reduces total error by 14.5% compared to the state-of-the-art method. It offers more reliable detection of the steady-state onset, delivering greater precision for benchmarking tasks. For users, the new approach enhances the accuracy and stability of performance benchmarking, efficiently handling diverse time series data. Its robustness and adaptability make it a valuable tool for real-world performance evaluation, ensuring consistent and reproducible results.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge