Almost-Optimal Local-Search Methods for Sparse Tensor PCA

Local-search methods are widely employed in statistical applications, yet interestingly, their theoretical foundations remain rather underexplored, compared to other classes of estimators such as low-degree polynomials and spectral methods. Of note, among the few existing results recent studies have revealed a significant "local-computational" gap in the context of a well-studied sparse tensor principal component analysis (PCA), where a broad class of local Markov chain methods exhibits a notable underperformance relative to other polynomial-time algorithms. In this work, we propose a series of local-search methods that provably "close" this gap to the best known polynomial-time procedures in multiple regimes of the model, including and going beyond the previously studied regimes in which the broad family of local Markov chain methods underperforms. Our framework includes: (1) standard greedy and randomized greedy algorithms applied to the (regularized) posterior of the model; and (2) novel random-threshold variants, in which the randomized greedy algorithm accepts a proposed transition if and only if the corresponding change in the Hamiltonian exceeds a random Gaussian threshold-rather that if and only if it is positive, as is customary. The introduction of the random thresholds enables a tight mathematical analysis of the randomized greedy algorithm's trajectory by crucially breaking the dependencies between the iterations, and could be of independent interest to the community.

Introducing Curvature to the Label Space

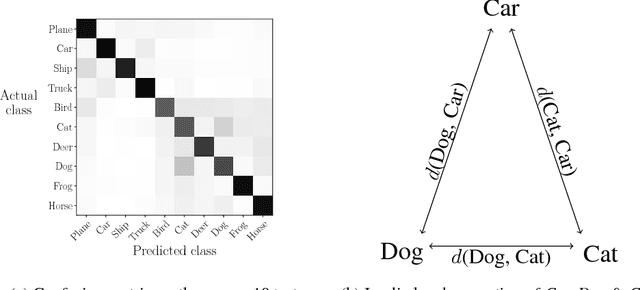
One-hot encoding is a labelling system that embeds classes as standard basis vectors in a label space. Despite seeing near-universal use in supervised categorical classification tasks, the scheme is problematic in its geometric implication that, as all classes are equally distant, all classes are equally different. This is inconsistent with most, if not all, real-world tasks due to the prevalence of ancestral and convergent relationships generating a varying degree of morphological similarity across classes. We address this issue by introducing curvature to the label-space using a metric tensor as a self-regulating method that better represents these relationships as a bolt-on, learning-algorithm agnostic solution. We propose both general constraints and specific statistical parameterizations of the metric and identify a direction for future research using autoencoder-based parameterizations.