Patrick Rebentrost
Accelerating Inference for Multilayer Neural Networks with Quantum Computers
Oct 08, 2025



Abstract:Fault-tolerant Quantum Processing Units (QPUs) promise to deliver exponential speed-ups in select computational tasks, yet their integration into modern deep learning pipelines remains unclear. In this work, we take a step towards bridging this gap by presenting the first fully-coherent quantum implementation of a multilayer neural network with non-linear activation functions. Our constructions mirror widely used deep learning architectures based on ResNet, and consist of residual blocks with multi-filter 2D convolutions, sigmoid activations, skip-connections, and layer normalizations. We analyse the complexity of inference for networks under three quantum data access regimes. Without any assumptions, we establish a quadratic speedup over classical methods for shallow bilinear-style networks. With efficient quantum access to the weights, we obtain a quartic speedup over classical methods. With efficient quantum access to both the inputs and the network weights, we prove that a network with an $N$-dimensional vectorized input, $k$ residual block layers, and a final residual-linear-pooling layer can be implemented with an error of $\epsilon$ with $O(\text{polylog}(N/\epsilon)^k)$ inference cost.
Artificial intelligence for representing and characterizing quantum systems
Sep 05, 2025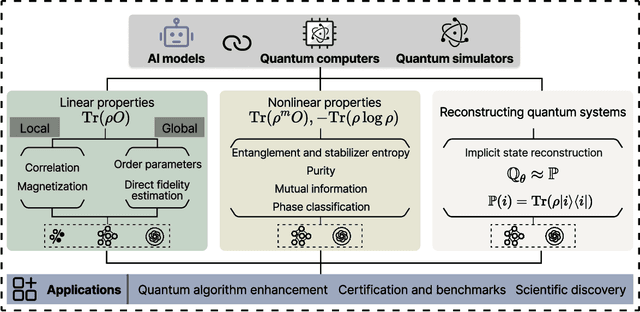

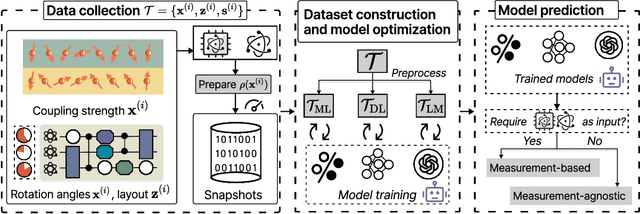
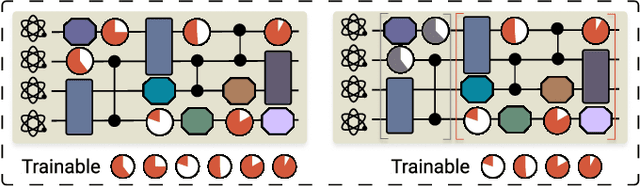
Abstract:Efficient characterization of large-scale quantum systems, especially those produced by quantum analog simulators and megaquop quantum computers, poses a central challenge in quantum science due to the exponential scaling of the Hilbert space with respect to system size. Recent advances in artificial intelligence (AI), with its aptitude for high-dimensional pattern recognition and function approximation, have emerged as a powerful tool to address this challenge. A growing body of research has leveraged AI to represent and characterize scalable quantum systems, spanning from theoretical foundations to experimental realizations. Depending on how prior knowledge and learning architectures are incorporated, the integration of AI into quantum system characterization can be categorized into three synergistic paradigms: machine learning, and, in particular, deep learning and language models. This review discusses how each of these AI paradigms contributes to two core tasks in quantum systems characterization: quantum property prediction and the construction of surrogates for quantum states. These tasks underlie diverse applications, from quantum certification and benchmarking to the enhancement of quantum algorithms and the understanding of strongly correlated phases of matter. Key challenges and open questions are also discussed, together with future prospects at the interface of AI and quantum science.
Degree-Optimized Cumulative Polynomial Kolmogorov-Arnold Networks
May 21, 2025Abstract:We introduce cumulative polynomial Kolmogorov-Arnold networks (CP-KAN), a neural architecture combining Chebyshev polynomial basis functions and quadratic unconstrained binary optimization (QUBO). Our primary contribution involves reformulating the degree selection problem as a QUBO task, reducing the complexity from $O(D^N)$ to a single optimization step per layer. This approach enables efficient degree selection across neurons while maintaining computational tractability. The architecture performs well in regression tasks with limited data, showing good robustness to input scales and natural regularization properties from its polynomial basis. Additionally, theoretical analysis establishes connections between CP-KAN's performance and properties of financial time series. Our empirical validation across multiple domains demonstrates competitive performance compared to several traditional architectures tested, especially in scenarios where data efficiency and numerical stability are important. Our implementation, including strategies for managing computational overhead in larger networks is available in Ref.~\citep{cpkan_implementation}.
Quantum Machine Learning: A Hands-on Tutorial for Machine Learning Practitioners and Researchers
Feb 03, 2025Abstract:This tutorial intends to introduce readers with a background in AI to quantum machine learning (QML) -- a rapidly evolving field that seeks to leverage the power of quantum computers to reshape the landscape of machine learning. For self-consistency, this tutorial covers foundational principles, representative QML algorithms, their potential applications, and critical aspects such as trainability, generalization, and computational complexity. In addition, practical code demonstrations are provided in https://qml-tutorial.github.io/ to illustrate real-world implementations and facilitate hands-on learning. Together, these elements offer readers a comprehensive overview of the latest advancements in QML. By bridging the gap between classical machine learning and quantum computing, this tutorial serves as a valuable resource for those looking to engage with QML and explore the forefront of AI in the quantum era.
Online Learning of Pure States is as Hard as Mixed States
Feb 02, 2025



Abstract:Quantum state tomography, the task of learning an unknown quantum state, is a fundamental problem in quantum information. In standard settings, the complexity of this problem depends significantly on the type of quantum state that one is trying to learn, with pure states being substantially easier to learn than general mixed states. A natural question is whether this separation holds for any quantum state learning setting. In this work, we consider the online learning framework and prove the surprising result that learning pure states in this setting is as hard as learning mixed states. More specifically, we show that both classes share almost the same sequential fat-shattering dimension, leading to identical regret scaling under the $L_1$-loss. We also generalize previous results on full quantum state tomography in the online setting to learning only partially the density matrix, using smooth analysis.
Quantum Algorithm for Sparse Online Learning with Truncated Gradient Descent
Nov 06, 2024
Abstract:Logistic regression, the Support Vector Machine (SVM), and least squares are well-studied methods in the statistical and computer science community, with various practical applications. High-dimensional data arriving on a real-time basis makes the design of online learning algorithms that produce sparse solutions essential. The seminal work of \hyperlink{cite.langford2009sparse}{Langford, Li, and Zhang (2009)} developed a method to obtain sparsity via truncated gradient descent, showing a near-optimal online regret bound. Based on this method, we develop a quantum sparse online learning algorithm for logistic regression, the SVM, and least squares. Given efficient quantum access to the inputs, we show that a quadratic speedup in the time complexity with respect to the dimension of the problem is achievable, while maintaining a regret of $O(1/\sqrt{T})$, where $T$ is the number of iterations.
Concept learning of parameterized quantum models from limited measurements
Aug 09, 2024Abstract:Classical learning of the expectation values of observables for quantum states is a natural variant of learning quantum states or channels. While learning-theoretic frameworks establish the sample complexity and the number of measurement shots per sample required for learning such statistical quantities, the interplay between these two variables has not been adequately quantified before. In this work, we take the probabilistic nature of quantum measurements into account in classical modelling and discuss these quantities under a single unified learning framework. We provide provable guarantees for learning parameterized quantum models that also quantify the asymmetrical effects and interplay of the two variables on the performance of learning algorithms. These results show that while increasing the sample size enhances the learning performance of classical machines, even with single-shot estimates, the improvements from increasing measurements become asymptotically trivial beyond a constant factor. We further apply our framework and theoretical guarantees to study the impact of measurement noise on the classical surrogation of parameterized quantum circuit models. Our work provides new tools to analyse the operational influence of finite measurement noise in the classical learning of quantum systems.
Efficient Quantum Circuits for Machine Learning Activation Functions including Constant T-depth ReLU
Apr 09, 2024



Abstract:In recent years, Quantum Machine Learning (QML) has increasingly captured the interest of researchers. Among the components in this domain, activation functions hold a fundamental and indispensable role. Our research focuses on the development of activation functions quantum circuits for integration into fault-tolerant quantum computing architectures, with an emphasis on minimizing $T$-depth. Specifically, we present novel implementations of ReLU and leaky ReLU activation functions, achieving constant $T$-depths of 4 and 8, respectively. Leveraging quantum lookup tables, we extend our exploration to other activation functions such as the sigmoid. This approach enables us to customize precision and $T$-depth by adjusting the number of qubits, making our results more adaptable to various application scenarios. This study represents a significant advancement towards enhancing the practicality and application of quantum machine learning.
Quantum linear algebra is all you need for Transformer architectures
Feb 26, 2024



Abstract:Generative machine learning methods such as large-language models are revolutionizing the creation of text and images. While these models are powerful they also harness a large amount of computational resources. The transformer is a key component in large language models that aims to generate a suitable completion of a given partial sequence. In this work, we investigate transformer architectures under the lens of fault-tolerant quantum computing. The input model is one where pre-trained weight matrices are given as block encodings to construct the query, key, and value matrices for the transformer. As a first step, we show how to prepare a block encoding of the self-attention matrix, with a row-wise application of the softmax function using the Hadamard product. In addition, we combine quantum subroutines to construct important building blocks in the transformer, the residual connection, layer normalization, and the feed-forward neural network. Our subroutines prepare an amplitude encoding of the transformer output, which can be measured to obtain a prediction. We discuss the potential and challenges for obtaining a quantum advantage.
Quantum Algorithms for the Pathwise Lasso
Dec 21, 2023


Abstract:We present a novel quantum high-dimensional linear regression algorithm with an $\ell_1$-penalty based on the classical LARS (Least Angle Regression) pathwise algorithm. Similarly to available classical numerical algorithms for Lasso, our quantum algorithm provides the full regularisation path as the penalty term varies, but quadratically faster per iteration under specific conditions. A quadratic speedup on the number of features/predictors $d$ is possible by using the simple quantum minimum-finding subroutine from D\"urr and Hoyer (arXiv'96) in order to obtain the joining time at each iteration. We then improve upon this simple quantum algorithm and obtain a quadratic speedup both in the number of features $d$ and the number of observations $n$ by using the recent approximate quantum minimum-finding subroutine from Chen and de Wolf (ICALP'23). As one of our main contributions, we construct a quantum unitary based on quantum amplitude estimation to approximately compute the joining times to be searched over by the approximate quantum minimum finding. Since the joining times are no longer exactly computed, it is no longer clear that the resulting approximate quantum algorithm obtains a good solution. As our second main contribution, we prove, via an approximate version of the KKT conditions and a duality gap, that the LARS algorithm (and therefore our quantum algorithm) is robust to errors. This means that it still outputs a path that minimises the Lasso cost function up to a small error if the joining times are only approximately computed. Finally, in the model where the observations are generated by an underlying linear model with an unknown coefficient vector, we prove bounds on the difference between the unknown coefficient vector and the approximate Lasso solution, which generalises known results about convergence rates in classical statistical learning theory analysis.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge