RocqSmith: Can Automatic Optimization Forge Better Proof Agents?

This work studies the applicability of automatic AI agent optimization methods to real-world agents in formal verification settings, focusing on automated theorem proving in Rocq as a representative and challenging domain. We evaluate how different automatic agent optimizers perform when applied to the task of optimizing a Rocq proof-generation agent, and assess whether parts of the fine-grained tuning of agentic systems, such as prompt design, contextual knowledge, and control strategies, can be automated. Our results show that while several optimizers yield measurable improvements, simple few-shot bootstrapping is the most consistently effective; however, none of the studied methods matches the performance of a carefully engineered state-of-the-art proof agent.

VERGE: Formal Refinement and Guidance Engine for Verifiable LLM Reasoning

Despite the syntactic fluency of Large Language Models (LLMs), ensuring their logical correctness in high-stakes domains remains a fundamental challenge. We present a neurosymbolic framework that combines LLMs with SMT solvers to produce verification-guided answers through iterative refinement. Our approach decomposes LLM outputs into atomic claims, autoformalizes them into first-order logic, and verifies their logical consistency using automated theorem proving. We introduce three key innovations: (1) multi-model consensus via formal semantic equivalence checking to ensure logic-level alignment between candidates, eliminating the syntactic bias of surface-form metrics, (2) semantic routing that directs different claim types to appropriate verification strategies: symbolic solvers for logical claims and LLM ensembles for commonsense reasoning, and (3) precise logical error localization via Minimal Correction Subsets (MCS), which pinpoint the exact subset of claims to revise, transforming binary failure signals into actionable feedback. Our framework classifies claims by their logical status and aggregates multiple verification signals into a unified score with variance-based penalty. The system iteratively refines answers using structured feedback until acceptance criteria are met or convergence is achieved. This hybrid approach delivers formal guarantees where possible and consensus verification elsewhere, advancing trustworthy AI. With the GPT-OSS-120B model, VERGE demonstrates an average performance uplift of 18.7% at convergence across a set of reasoning benchmarks compared to single-pass approaches.

Neural Theorem Proving for Verification Conditions: A Real-World Benchmark

Theorem proving is fundamental to program verification, where the automated proof of Verification Conditions (VCs) remains a primary bottleneck. Real-world program verification frequently encounters hard VCs that existing Automated Theorem Provers (ATPs) cannot prove, leading to a critical need for extensive manual proofs that burden practical application. While Neural Theorem Proving (NTP) has achieved significant success in mathematical competitions, demonstrating the potential of machine learning approaches to formal reasoning, its application to program verification--particularly VC proving--remains largely unexplored. Despite existing work on annotation synthesis and verification-related theorem proving, no benchmark has specifically targeted this fundamental bottleneck: automated VC proving. This work introduces Neural Theorem Proving for Verification Conditions (NTP4VC), presenting the first real-world multi-language benchmark for this task. From real-world projects such as Linux and Contiki-OS kernel, our benchmark leverages industrial pipelines (Why3 and Frama-C) to generate semantically equivalent test cases across formal languages of Isabelle, Lean, and Rocq. We evaluate large language models (LLMs), both general-purpose and those fine-tuned for theorem proving, on NTP4VC. Results indicate that although LLMs show promise in VC proving, significant challenges remain for program verification, highlighting a large gap and opportunity for future research.

Quantum automated theorem proving

Automated theorem proving, or more broadly automated reasoning, aims at using computer programs to automatically prove or disprove mathematical theorems and logical statements. It takes on an essential role across a vast array of applications and the quest for enhanced theorem-proving capabilities remains a prominent pursuit in artificial intelligence. Here, we propose a generic framework for quantum automated theorem proving, where the intrinsic quantum superposition and entanglement features would lead to potential advantages. In particular, we introduce quantum representations of knowledge bases and propose corresponding reasoning algorithms for a variety of tasks. We show how automated reasoning can be achieved with quantum resolution in both propositional and first-order logic with quadratically reduced query complexity. In addition, we propose the quantum algebraic proving method for geometric theorems, extending Wu's algebraic approach beyond the classical setting. Through concrete examples, including geometry problems from the International Mathematical Olympiad, we demonstrate how a quantum computer may prove geometric theorems with quadratic better query complexity. Our results establish a primary approach towards building quantum automatic theorem provers, which would be crucial for practical applications of both near-term and future quantum technologies.

GDEPO: Group Dual-dynamic and Equal-right-advantage Policy Optimization with Enhanced Training Data Utilization for Sample-Constrained Reinforcement Learning

Automated Theorem Proving (ATP) represents a fundamental challenge in Artificial Intelligence (AI), requiring the construction of machine-verifiable proofs in formal languages such as Lean to evaluate AI reasoning capabilities. Reinforcement learning (RL), particularly the high-performance Group Relative Policy Optimization (GRPO) algorithm, has emerged as a mainstream approach for this task. However, in ATP scenarios, GRPO faces two critical issues: when composite rewards are used, its relative advantage estimation may conflict with the binary feedback from the formal verifier; meanwhile, its static sampling strategy may discard entire batches of data if no valid proof is found, resulting in zero contribution to model updates and significant data waste. To address these limitations, we propose Group Dual-dynamic and Equal-right-advantage Policy Optimization (GDEPO), a method incorporating three core mechanisms: 1) dynamic additional sampling, which resamples invalid batches until a valid proof is discovered; 2) equal-right advantage, decoupling the sign of the advantage function (based on correctness) from its magnitude (modulated by auxiliary rewards) to ensure stable and correct policy updates; and 3) dynamic additional iterations, applying extra gradient steps to initially failed but eventually successful samples to accelerate learning on challenging cases. Experiments conducted on three datasets of varying difficulty (MinF2F-test, MathOlympiadBench, PutnamBench) confirm the effectiveness of GDEPO, while ablation studies validate the necessity of its synergistic components. The proposed method enhances data utilization and optimization efficiency, offering a novel training paradigm for ATP.

Imandra CodeLogician: Neuro-Symbolic Reasoning for Precise Analysis of Software Logic

Large Language Models (LLMs) have shown strong performance on code understanding tasks, yet they fundamentally lack the ability to perform precise, exhaustive mathematical reasoning about program behavior. Existing benchmarks either focus on mathematical proof automation, largely disconnected from real-world software, or on engineering tasks that do not require semantic rigor. We present CodeLogician, a neurosymbolic agent for precise analysis of software logic, integrated with ImandraX, an industrial automated reasoning engine deployed in financial markets and safety-critical systems. Unlike prior approaches that use formal methods primarily to validate LLM outputs, CodeLogician uses LLMs to construct explicit formal models of software systems, enabling automated reasoning to answer rich semantic questions beyond binary verification outcomes. To rigorously evaluate mathematical reasoning about software logic, we introduce code-logic-bench, a benchmark targeting the middle ground between theorem proving and software engineering benchmarks. It measures reasoning correctness about program state spaces, control flow, coverage constraints, and edge cases, with ground truth defined via formal modeling and region decomposition. Comparing LLM-only reasoning against LLMs augmented with CodeLogician, formal augmentation yields substantial improvements, closing a 41-47 percentage point gap in reasoning accuracy. These results demonstrate that neurosymbolic integration is essential for scaling program analysis toward rigorous, autonomous software understanding.

Vibe Coding an LLM-powered Theorem Prover

We present Isabellm, an LLM-powered theorem prover for Isabelle/HOL that performs fully automatic proof synthesis. Isabellm works with any local LLM on Ollama and APIs such as Gemini CLI, and it is designed to run on consumer grade computers. The system combines a stepwise prover, which uses large language models to propose proof commands validated by Isabelle in a bounded search loop, with a higher-level proof planner that generates structured Isar outlines and attempts to fill and repair remaining gaps. The framework includes beam search for tactics, tactics reranker ML and RL models, premise selection with small transformer models, micro-RAG for Isar proofs built from AFP, and counter-example guided proof repair. All the code is implemented by GPT 4.1 - 5.2, Gemini 3 Pro, and Claude 4.5. Empirically, Isabellm can prove certain lemmas that defeat Isabelle's standard automation, including Sledgehammer, demonstrating the practical value of LLM-guided proof search. At the same time, we find that even state-of-the-art LLMs, such as GPT 5.2 Extended Thinking and Gemini 3 Pro struggle to reliably implement the intended fill-and-repair mechanisms with complex algorithmic designs, highlighting fundamental challenges in LLM code generation and reasoning. The code of Isabellm is available at https://github.com/zhehou/llm-isabelle

CutisAI: Deep Learning Framework for Automated Dermatology and Cancer Screening

The rapid growth of dermatological imaging and mobile diagnostic tools calls for systems that not only demonstrate empirical performance but also provide strong theoretical guarantees. Deep learning models have shown high predictive accuracy; however, they are often criticized for lacking well, calibrated uncertainty estimates without which these models are hardly deployable in a clinical setting. To this end, we present the Conformal Bayesian Dermatological Classifier (CBDC), a well, founded framework that combines Statistical Learning Theory, Topological Data Analysis (TDA), and Bayesian Conformal Inference. CBDC offers distribution, dependent generalization bounds that reflect dermatological variability, proves a topological stability theorem that guarantees the invariance of convolutional neural network embeddings under photometric and morphological perturbations and provides finite conformal coverage guarantees for trustworthy uncertainty quantification. Through exhaustive experiments on the HAM10000, PH2, and ISIC 2020 datasets, we show that CBDC not only attains classification accuracy but also generates calibrated predictions that are interpretable from a clinical perspective. This research constitutes a theoretical and practical leap for deep dermatological diagnostics, thereby opening the machine learning theory clinical applicability interface.

MSC-180: A Benchmark for Automated Formal Theorem Proving from Mathematical Subject Classification

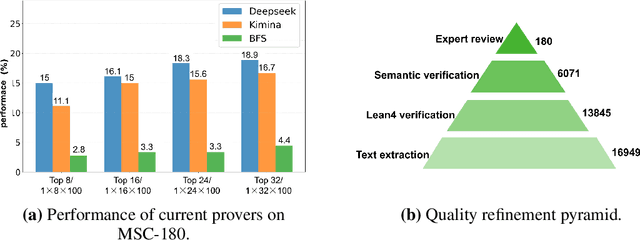
Automated Theorem Proving (ATP) represents a core research direction in artificial intelligence for achieving formal reasoning and verification, playing a significant role in advancing machine intelligence. However, current large language model (LLM)-based theorem provers suffer from limitations such as restricted domain coverage and weak generalization in mathematical reasoning. To address these issues, we propose MSC-180, a benchmark for evaluation based on the MSC2020 mathematical subject classification. It comprises 180 formal verification problems, 3 advanced problems from each of 60 mathematical branches, spanning from undergraduate to graduate levels. Each problem has undergone multiple rounds of verification and refinement by domain experts to ensure formal accuracy. Evaluations of state-of-the-art LLM-based theorem provers under the pass@32 setting reveal that the best model achieves only an 18.89% overall pass rate, with prominent issues including significant domain bias (maximum domain coverage 41.7%) and a difficulty gap (significantly lower pass rates on graduate-level problems). To further quantify performance variability across mathematical domains, we introduce the coefficient of variation (CV) as an evaluation metric. The observed CV values are 4-6 times higher than the statistical high-variability threshold, indicating that the models still rely on pattern matching from training corpora rather than possessing transferable reasoning mechanisms and systematic generalization capabilities. MSC-180, together with its multi-dimensional evaluation framework, provides a discriminative and systematic benchmark for driving the development of next-generation AI systems with genuine mathematical reasoning abilities.

Gödel's Poetry

Formal, automated theorem proving has long been viewed as a challenge to artificial intelligence. We introduce here a new approach to computer theorem proving, one that employs specialized language models for Lean4 proof generation combined with recursive decomposition of difficult theorems into simpler entailing propositions. These models are coordinated through a multi-agent architecture that orchestrates autoformalization (if required), proof generation, decomposition of difficult theorems into simpler entailing propositions, and recursive proof (and/or decomposition) of these propositions. Without decomposition, we achieve a 90.4% pass rate on miniF2F. With decomposition, this is significantly improved. A key technical contribution lies in our extension of the Kimina Lean Server with abstract syntax tree (AST) parsing capabilities to facilitate automated, recursive proof decomposition. The system is made available on PyPI as goedels-poetry (at https://pypi.org/project/goedels-poetry ), and the open-source implementation KellyJDavis/goedels-poetry (at https://github.com/KellyJDavis/goedels-poetry ) facilitates both adaptation to alternative language models and extension with custom functionality.