Subtyping in DHOL -- Extended preprint

The recently introduced dependent typed higher-order logic (DHOL) offers an interesting compromise between expressiveness and automation support. It sacrifices the decidability of its type system in order to significantly extend its expressiveness over standard HOL. Yet it retains strong automated theorem proving support via a sound and complete translation to HOL. We leverage this design to extend DHOL with refinement and quotient types. Both of these are commonly requested by practitioners but rarely provided by automated theorem provers. This is because they inherently require undecidable typing and thus are very difficult to retrofit to decidable type systems. But with DHOL already doing the heavy lifting, adding them is not only possible but elegant and simple. Concretely, we add refinement and quotient types as special cases of subtyping. This turns the associated canonical inclusion resp. projection maps into identity maps and thus avoids costly changes in representation. We present the syntax, semantics, and translation to HOL for the extended language, including the proofs of soundness and completeness.

Theorem Proving in Dependently-Typed Higher-Order Logic -- Extended Preprint

Higher-order logic HOL offers a very simple syntax and semantics for representing and reasoning about typed data structures. But its type system lacks advanced features where types may depend on terms. Dependent type theory offers such a rich type system, but has rather substantial conceptual differences to HOL, as well as comparatively poor proof automation support. We introduce a dependently-typed extension DHOL of HOL that retains the style and conceptual framework of HOL. Moreover, we build a translation from DHOL to HOL and implement it as a preprocessor to a HOL theorem prover, thereby obtaining a theorem prover for DHOL.

Big Math and the One-Brain Barrier A Position Paper and Architecture Proposal

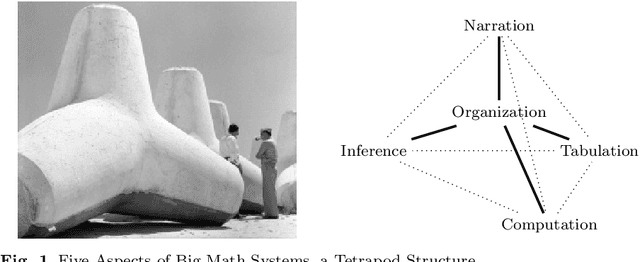
Over the last decades, a class of important mathematical results have required an ever increasing amount of human effort to carry out. For some, the help of computers is now indispensable. We analyze the implications of this trend towards "big mathematics", its relation to human cognition, and how machine support for big math can be organized. The central contribution of this position paper is an information model for "doing mathematics", which posits that humans very efficiently integrate four aspects: inference, computation, tabulation, and narration around a well-organized core of mathematical knowledge. The challenge for mathematical software systems is that these four aspects need to be integrated as well. We briefly survey the state of the art.

Publishing Math Lecture Notes as Linked Data

We mark up a corpus of LaTeX lecture notes semantically and expose them as Linked Data in XHTML+MathML+RDFa. Our application makes the resulting documents interactively browsable for students. Our ontology helps to answer queries from students and lecturers, and paves the path towards an integration of our corpus with external sites.