Zhihong Shao
DeepSeek-Prover-V2: Advancing Formal Mathematical Reasoning via Reinforcement Learning for Subgoal Decomposition
Apr 30, 2025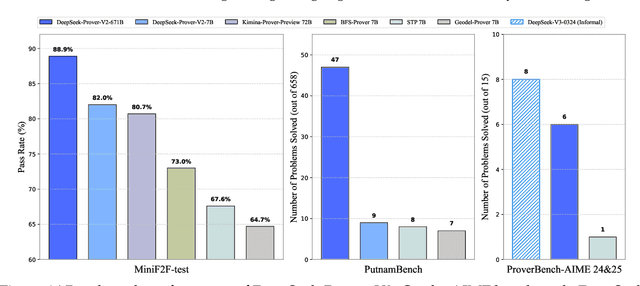



Abstract:We introduce DeepSeek-Prover-V2, an open-source large language model designed for formal theorem proving in Lean 4, with initialization data collected through a recursive theorem proving pipeline powered by DeepSeek-V3. The cold-start training procedure begins by prompting DeepSeek-V3 to decompose complex problems into a series of subgoals. The proofs of resolved subgoals are synthesized into a chain-of-thought process, combined with DeepSeek-V3's step-by-step reasoning, to create an initial cold start for reinforcement learning. This process enables us to integrate both informal and formal mathematical reasoning into a unified model. The resulting model, DeepSeek-Prover-V2-671B, achieves state-of-the-art performance in neural theorem proving, reaching 88.9% pass ratio on the MiniF2F-test and solving 49 out of 658 problems from PutnamBench. In addition to standard benchmarks, we introduce ProverBench, a collection of 325 formalized problems, to enrich our evaluation, including 15 selected problems from the recent AIME competitions (years 24-25). Further evaluation on these 15 AIME problems shows that the model successfully solves 6 of them. In comparison, DeepSeek-V3 solves 8 of these problems using majority voting, highlighting that the gap between formal and informal mathematical reasoning in large language models is substantially narrowing.
DeepSeek-V3 Technical Report
Dec 27, 2024



Abstract:We present DeepSeek-V3, a strong Mixture-of-Experts (MoE) language model with 671B total parameters with 37B activated for each token. To achieve efficient inference and cost-effective training, DeepSeek-V3 adopts Multi-head Latent Attention (MLA) and DeepSeekMoE architectures, which were thoroughly validated in DeepSeek-V2. Furthermore, DeepSeek-V3 pioneers an auxiliary-loss-free strategy for load balancing and sets a multi-token prediction training objective for stronger performance. We pre-train DeepSeek-V3 on 14.8 trillion diverse and high-quality tokens, followed by Supervised Fine-Tuning and Reinforcement Learning stages to fully harness its capabilities. Comprehensive evaluations reveal that DeepSeek-V3 outperforms other open-source models and achieves performance comparable to leading closed-source models. Despite its excellent performance, DeepSeek-V3 requires only 2.788M H800 GPU hours for its full training. In addition, its training process is remarkably stable. Throughout the entire training process, we did not experience any irrecoverable loss spikes or perform any rollbacks. The model checkpoints are available at https://github.com/deepseek-ai/DeepSeek-V3.
DeepSeek-Prover-V1.5: Harnessing Proof Assistant Feedback for Reinforcement Learning and Monte-Carlo Tree Search
Aug 15, 2024



Abstract:We introduce DeepSeek-Prover-V1.5, an open-source language model designed for theorem proving in Lean 4, which enhances DeepSeek-Prover-V1 by optimizing both training and inference processes. Pre-trained on DeepSeekMath-Base with specialization in formal mathematical languages, the model undergoes supervised fine-tuning using an enhanced formal theorem proving dataset derived from DeepSeek-Prover-V1. Further refinement is achieved through reinforcement learning from proof assistant feedback (RLPAF). Beyond the single-pass whole-proof generation approach of DeepSeek-Prover-V1, we propose RMaxTS, a variant of Monte-Carlo tree search that employs an intrinsic-reward-driven exploration strategy to generate diverse proof paths. DeepSeek-Prover-V1.5 demonstrates significant improvements over DeepSeek-Prover-V1, achieving new state-of-the-art results on the test set of the high school level miniF2F benchmark ($63.5\%$) and the undergraduate level ProofNet benchmark ($25.3\%$).
DeepSeek-Coder-V2: Breaking the Barrier of Closed-Source Models in Code Intelligence
Jun 17, 2024



Abstract:We present DeepSeek-Coder-V2, an open-source Mixture-of-Experts (MoE) code language model that achieves performance comparable to GPT4-Turbo in code-specific tasks. Specifically, DeepSeek-Coder-V2 is further pre-trained from an intermediate checkpoint of DeepSeek-V2 with additional 6 trillion tokens. Through this continued pre-training, DeepSeek-Coder-V2 substantially enhances the coding and mathematical reasoning capabilities of DeepSeek-V2, while maintaining comparable performance in general language tasks. Compared to DeepSeek-Coder-33B, DeepSeek-Coder-V2 demonstrates significant advancements in various aspects of code-related tasks, as well as reasoning and general capabilities. Additionally, DeepSeek-Coder-V2 expands its support for programming languages from 86 to 338, while extending the context length from 16K to 128K. In standard benchmark evaluations, DeepSeek-Coder-V2 achieves superior performance compared to closed-source models such as GPT4-Turbo, Claude 3 Opus, and Gemini 1.5 Pro in coding and math benchmarks.
Learning Task Decomposition to Assist Humans in Competitive Programming
Jun 07, 2024



Abstract:When using language models (LMs) to solve complex problems, humans might struggle to understand the LM-generated solutions and repair the flawed ones. To assist humans in repairing them, we propose to automatically decompose complex solutions into multiple simpler pieces that correspond to specific subtasks. We introduce a novel objective for learning task decomposition, termed assistive value (AssistV), which measures the feasibility and speed for humans to repair the decomposed solution. We collect a dataset of human repair experiences on different decomposed solutions. Utilizing the collected data as in-context examples, we then learn to critique, refine, and rank decomposed solutions to improve AssistV. We validate our method under competitive programming problems: under 177 hours of human study, our method enables non-experts to solve 33.3\% more problems, speeds them up by 3.3x, and empowers them to match unassisted experts.
DeepSeek-Prover: Advancing Theorem Proving in LLMs through Large-Scale Synthetic Data
May 23, 2024



Abstract:Proof assistants like Lean have revolutionized mathematical proof verification, ensuring high accuracy and reliability. Although large language models (LLMs) show promise in mathematical reasoning, their advancement in formal theorem proving is hindered by a lack of training data. To address this issue, we introduce an approach to generate extensive Lean 4 proof data derived from high-school and undergraduate-level mathematical competition problems. This approach involves translating natural language problems into formal statements, filtering out low-quality statements, and generating proofs to create synthetic data. After fine-tuning the DeepSeekMath 7B model on this synthetic dataset, which comprises 8 million formal statements with proofs, our model achieved whole-proof generation accuracies of 46.3% with 64 samples and 52% cumulatively on the Lean 4 miniF2F test, surpassing the baseline GPT-4 at 23.0% with 64 samples and a tree search reinforcement learning method at 41.0%. Additionally, our model successfully proved 5 out of 148 problems in the Lean 4 Formalized International Mathematical Olympiad (FIMO) benchmark, while GPT-4 failed to prove any. These results demonstrate the potential of leveraging large-scale synthetic data to enhance theorem-proving capabilities in LLMs. Both the synthetic dataset and the model will be made available to facilitate further research in this promising field.
DeepSeekMath: Pushing the Limits of Mathematical Reasoning in Open Language Models
Feb 06, 2024



Abstract:Mathematical reasoning poses a significant challenge for language models due to its complex and structured nature. In this paper, we introduce DeepSeekMath 7B, which continues pre-training DeepSeek-Coder-Base-v1.5 7B with 120B math-related tokens sourced from Common Crawl, together with natural language and code data. DeepSeekMath 7B has achieved an impressive score of 51.7% on the competition-level MATH benchmark without relying on external toolkits and voting techniques, approaching the performance level of Gemini-Ultra and GPT-4. Self-consistency over 64 samples from DeepSeekMath 7B achieves 60.9% on MATH. The mathematical reasoning capability of DeepSeekMath is attributed to two key factors: First, we harness the significant potential of publicly available web data through a meticulously engineered data selection pipeline. Second, we introduce Group Relative Policy Optimization (GRPO), a variant of Proximal Policy Optimization (PPO), that enhances mathematical reasoning abilities while concurrently optimizing the memory usage of PPO.
DeepSeek LLM: Scaling Open-Source Language Models with Longtermism
Jan 05, 2024



Abstract:The rapid development of open-source large language models (LLMs) has been truly remarkable. However, the scaling law described in previous literature presents varying conclusions, which casts a dark cloud over scaling LLMs. We delve into the study of scaling laws and present our distinctive findings that facilitate scaling of large scale models in two commonly used open-source configurations, 7B and 67B. Guided by the scaling laws, we introduce DeepSeek LLM, a project dedicated to advancing open-source language models with a long-term perspective. To support the pre-training phase, we have developed a dataset that currently consists of 2 trillion tokens and is continuously expanding. We further conduct supervised fine-tuning (SFT) and Direct Preference Optimization (DPO) on DeepSeek LLM Base models, resulting in the creation of DeepSeek Chat models. Our evaluation results demonstrate that DeepSeek LLM 67B surpasses LLaMA-2 70B on various benchmarks, particularly in the domains of code, mathematics, and reasoning. Furthermore, open-ended evaluations reveal that DeepSeek LLM 67B Chat exhibits superior performance compared to GPT-3.5.
Math-Shepherd: Verify and Reinforce LLMs Step-by-step without Human Annotations
Dec 28, 2023



Abstract:In this paper, we present an innovative process-oriented math process reward model called \textbf{Math-Shepherd}, which assigns a reward score to each step of math problem solutions. The training of Math-Shepherd is achieved using automatically constructed process-wise supervision data, breaking the bottleneck of heavy reliance on manual annotation in existing work. We explore the effectiveness of Math-Shepherd in two scenarios: 1) \textit{Verification}: Math-Shepherd is utilized for reranking multiple outputs generated by Large Language Models (LLMs); 2) \textit{Reinforcement Learning}: Math-Shepherd is employed to reinforce LLMs with step-by-step Proximal Policy Optimization (PPO). With Math-Shepherd, a series of open-source LLMs demonstrates exceptional performance. For instance, the step-by-step PPO with Math-Shepherd significantly improves the accuracy of Mistral-7B (77.9\%$\to$84.1\% on GSM8K and 28.6\%$\to$33.0\% on MATH). The accuracy can be further enhanced to 89.1\% and 43.5\% on GSM8K and MATH with the verification of Math-Shepherd, respectively. We believe that automatic process supervision holds significant potential for the future evolution of LLMs.
ToRA: A Tool-Integrated Reasoning Agent for Mathematical Problem Solving
Oct 04, 2023



Abstract:Large language models have made significant progress in various language tasks, yet they still struggle with complex mathematics. In this paper, we propose ToRA a series of Tool-integrated Reasoning Agents designed to solve challenging mathematical problems by seamlessly integrating natural language reasoning with the utilization of external tools (e.g., computation libraries and symbolic solvers), thereby amalgamating the analytical prowess of language and the computational efficiency of tools. To train ToRA, we curate interactive tool-use trajectories on mathematical datasets, apply imitation learning on the annotations, and propose output space shaping to further refine models' reasoning behavior. As a result, ToRA models significantly outperform open-source models on 10 mathematical reasoning datasets across all scales with 13%-19% absolute improvements on average. Notably, ToRA-7B reaches 44.6% on the competition-level dataset MATH, surpassing the best open-source model WizardMath-70B by 22% absolute. ToRA-Code-34B is also the first open-source model that achieves an accuracy exceeding 50% on MATH, which significantly outperforms GPT-4's CoT result, and is competitive with GPT-4 solving problems with programs. Additionally, we conduct a comprehensive analysis of the benefits and remaining challenges of tool interaction for mathematical reasoning, providing valuable insights for future research.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge