Pseudo-Asynchronous Local SGD: Robust and Efficient Data-Parallel Training

Following AI scaling trends, frontier models continue to grow in size and continue to be trained on larger datasets. Training these models requires huge investments in exascale computational resources, which has in turn driven development of distributed deep learning methods. Data parallelism is an essential approach to speed up training, but it requires frequent global communication between workers, which can bottleneck training at the largest scales. In this work, we propose a method called Pseudo-Asynchronous Local SGD (PALSGD) to improve the efficiency of data-parallel training. PALSGD is an extension of Local SGD (Stich, 2018) and DiLoCo (Douillard et al., 2023), designed to further reduce communication frequency by introducing a pseudo-synchronization mechanism. PALSGD allows the use of longer synchronization intervals compared to standard Local SGD. Despite the reduced communication frequency, the pseudo-synchronization approach ensures that model consistency is maintained, leading to performance results comparable to those achieved with more frequent synchronization. Furthermore, we provide a theoretical analysis of PALSGD, establishing its convergence and deriving its convergence rate. This analysis offers insights into the algorithm's behavior and performance guarantees. We evaluated PALSGD on image classification and language modeling tasks. Our results show that PALSGD achieves better performance in less time compared to existing methods like Distributed Data Parallel (DDP), and DiLoCo. Notably, PALSGD trains 18.4% faster than DDP on ImageNet-1K with ResNet-50, 24.4% faster than DDP on TinyStories with GPT-Neo125M, and 21.1% faster than DDP on TinyStories with GPT-Neo-8M.

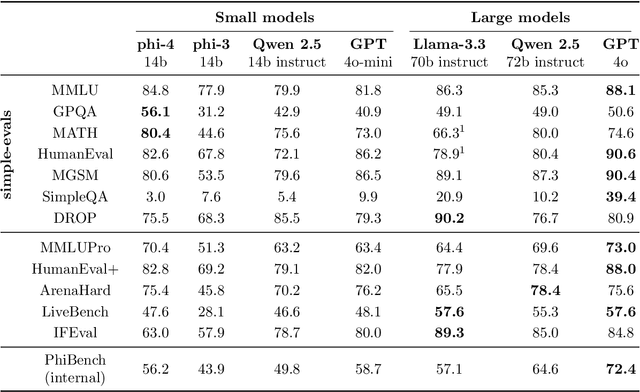
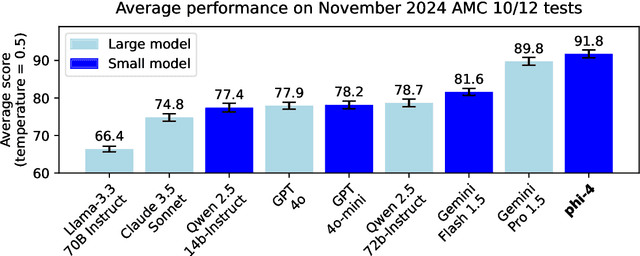
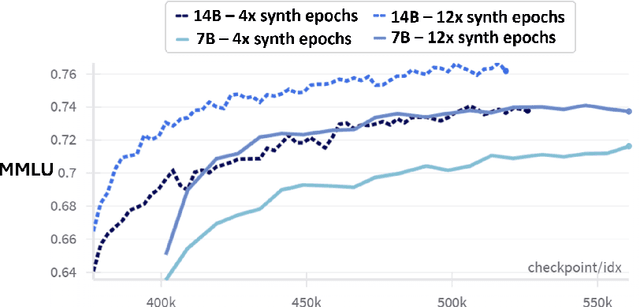
Phi-4 Technical Report

We present phi-4, a 14-billion parameter language model developed with a training recipe that is centrally focused on data quality. Unlike most language models, where pre-training is based primarily on organic data sources such as web content or code, phi-4 strategically incorporates synthetic data throughout the training process. While previous models in the Phi family largely distill the capabilities of a teacher model (specifically GPT-4), phi-4 substantially surpasses its teacher model on STEM-focused QA capabilities, giving evidence that our data-generation and post-training techniques go beyond distillation. Despite minimal changes to the phi-3 architecture, phi-4 achieves strong performance relative to its size -- especially on reasoning-focused benchmarks -- due to improved data, training curriculum, and innovations in the post-training scheme.

Phi-3 Technical Report: A Highly Capable Language Model Locally on Your Phone

We introduce phi-3-mini, a 3.8 billion parameter language model trained on 3.3 trillion tokens, whose overall performance, as measured by both academic benchmarks and internal testing, rivals that of models such as Mixtral 8x7B and GPT-3.5 (e.g., phi-3-mini achieves 69% on MMLU and 8.38 on MT-bench), despite being small enough to be deployed on a phone. The innovation lies entirely in our dataset for training, a scaled-up version of the one used for phi-2, composed of heavily filtered web data and synthetic data. The model is also further aligned for robustness, safety, and chat format. We also provide some initial parameter-scaling results with a 7B and 14B models trained for 4.8T tokens, called phi-3-small and phi-3-medium, both significantly more capable than phi-3-mini (e.g., respectively 75% and 78% on MMLU, and 8.7 and 8.9 on MT-bench).

Differentially Private Synthetic Data via Foundation Model APIs 2: Text

Text data has become extremely valuable due to the emergence of machine learning algorithms that learn from it. A lot of high-quality text data generated in the real world is private and therefore cannot be shared or used freely due to privacy concerns. Generating synthetic replicas of private text data with a formal privacy guarantee, i.e., differential privacy (DP), offers a promising and scalable solution. However, existing methods necessitate DP finetuning of large language models (LLMs) on private data to generate DP synthetic data. This approach is not viable for proprietary LLMs (e.g., GPT-3.5) and also demands considerable computational resources for open-source LLMs. Lin et al. (2024) recently introduced the Private Evolution (PE) algorithm to generate DP synthetic images with only API access to diffusion models. In this work, we propose an augmented PE algorithm, named Aug-PE, that applies to the complex setting of text. We use API access to an LLM and generate DP synthetic text without any model training. We conduct comprehensive experiments on three benchmark datasets. Our results demonstrate that Aug-PE produces DP synthetic text that yields competitive utility with the SOTA DP finetuning baselines. This underscores the feasibility of relying solely on API access of LLMs to produce high-quality DP synthetic texts, thereby facilitating more accessible routes to privacy-preserving LLM applications. Our code and data are available at https://github.com/AI-secure/aug-pe.

Can Generalist Foundation Models Outcompete Special-Purpose Tuning? Case Study in Medicine

Generalist foundation models such as GPT-4 have displayed surprising capabilities in a wide variety of domains and tasks. Yet, there is a prevalent assumption that they cannot match specialist capabilities of fine-tuned models. For example, most explorations to date on medical competency benchmarks have leveraged domain-specific training, as exemplified by efforts on BioGPT and Med-PaLM. We build on a prior study of GPT-4's capabilities on medical challenge benchmarks in the absence of special training. Rather than using simple prompting to highlight the model's out-of-the-box capabilities, we perform a systematic exploration of prompt engineering. We find that prompting innovation can unlock deeper specialist capabilities and show that GPT-4 easily tops prior leading results for medical benchmarks. The prompting methods we explore are general purpose, and make no specific use of domain expertise, removing the need for expert-curated content. Our experimental design carefully controls for overfitting during the prompt engineering process. We introduce Medprompt, based on a composition of several prompting strategies. With Medprompt, GPT-4 achieves state-of-the-art results on all nine of the benchmark datasets in the MultiMedQA suite. The method outperforms leading specialist models such as Med-PaLM 2 by a significant margin with an order of magnitude fewer calls to the model. Steering GPT-4 with Medprompt achieves a 27% reduction in error rate on the MedQA dataset over the best methods to date achieved with specialist models and surpasses a score of 90% for the first time. Beyond medical problems, we show the power of Medprompt to generalize to other domains and provide evidence for the broad applicability of the approach via studies of the strategy on exams in electrical engineering, machine learning, philosophy, accounting, law, nursing, and clinical psychology.

Positional Description Matters for Transformers Arithmetic

Transformers, central to the successes in modern Natural Language Processing, often falter on arithmetic tasks despite their vast capabilities --which paradoxically include remarkable coding abilities. We observe that a crucial challenge is their naive reliance on positional information to solve arithmetic problems with a small number of digits, leading to poor performance on larger numbers. Herein, we delve deeper into the role of positional encoding, and propose several ways to fix the issue, either by modifying the positional encoding directly, or by modifying the representation of the arithmetic task to leverage standard positional encoding differently. We investigate the value of these modifications for three tasks: (i) classical multiplication, (ii) length extrapolation in addition, and (iii) addition in natural language context. For (i) we train a small model on a small dataset (100M parameters and 300k samples) with remarkable aptitude in (direct, no scratchpad) 15 digits multiplication and essentially perfect up to 12 digits, while usual training in this context would give a model failing at 4 digits multiplication. In the experiments on addition, we use a mere 120k samples to demonstrate: for (ii) extrapolation from 10 digits to testing on 12 digits numbers while usual training would have no extrapolation, and for (iii) almost perfect accuracy up to 5 digits while usual training would be correct only up to 3 digits (which is essentially memorization with a training set of 120k samples).

Textbooks Are All You Need II: phi-1.5 technical report

We continue the investigation into the power of smaller Transformer-based language models as initiated by \textbf{TinyStories} -- a 10 million parameter model that can produce coherent English -- and the follow-up work on \textbf{phi-1}, a 1.3 billion parameter model with Python coding performance close to the state-of-the-art. The latter work proposed to use existing Large Language Models (LLMs) to generate ``textbook quality" data as a way to enhance the learning process compared to traditional web data. We follow the ``Textbooks Are All You Need" approach, focusing this time on common sense reasoning in natural language, and create a new 1.3 billion parameter model named \textbf{phi-1.5}, with performance on natural language tasks comparable to models 5x larger, and surpassing most non-frontier LLMs on more complex reasoning tasks such as grade-school mathematics and basic coding. More generally, \textbf{phi-1.5} exhibits many of the traits of much larger LLMs, both good -- such as the ability to ``think step by step" or perform some rudimentary in-context learning -- and bad, including hallucinations and the potential for toxic and biased generations -- encouragingly though, we are seeing improvement on that front thanks to the absence of web data. We open-source \textbf{phi-1.5} to promote further research on these urgent topics.

Textbooks Are All You Need

We introduce phi-1, a new large language model for code, with significantly smaller size than competing models: phi-1 is a Transformer-based model with 1.3B parameters, trained for 4 days on 8 A100s, using a selection of ``textbook quality" data from the web (6B tokens) and synthetically generated textbooks and exercises with GPT-3.5 (1B tokens). Despite this small scale, phi-1 attains pass@1 accuracy 50.6% on HumanEval and 55.5% on MBPP. It also displays surprising emergent properties compared to phi-1-base, our model before our finetuning stage on a dataset of coding exercises, and phi-1-small, a smaller model with 350M parameters trained with the same pipeline as phi-1 that still achieves 45% on HumanEval.

An Empirical Study on Challenging Math Problem Solving with GPT-4

Employing Large Language Models (LLMs) to address mathematical problems is an intriguing research endeavor, considering the abundance of math problems expressed in natural language across numerous science and engineering fields. While several prior works have investigated solving elementary mathematics using LLMs, this work explores the frontier of using GPT-4 for solving more complex and challenging math problems. We evaluate various ways of using GPT-4. Some of them are adapted from existing work, and one is MathChat, a conversational problem-solving framework newly proposed in this work. We perform the evaluation on difficult high school competition problems from the MATH dataset, which shows the advantage of the proposed conversational approach.

Automatic Prompt Optimization with "Gradient Descent" and Beam Search

Large Language Models (LLMs) have shown impressive performance as general purpose agents, but their abilities remain highly dependent on prompts which are hand written with onerous trial-and-error effort. We propose a simple and nonparametric solution to this problem, Automatic Prompt Optimization (APO), which is inspired by numerical gradient descent to automatically improve prompts, assuming access to training data and an LLM API. The algorithm uses minibatches of data to form natural language ``gradients'' that criticize the current prompt. The gradients are then ``propagated'' into the prompt by editing the prompt in the opposite semantic direction of the gradient. These gradient descent steps are guided by a beam search and bandit selection procedure which significantly improves algorithmic efficiency. Preliminary results across three benchmark NLP tasks and the novel problem of LLM jailbreak detection suggest that Automatic Prompt Optimization can outperform prior prompt editing techniques and improve an initial prompt's performance by up to 31\%, by using data to rewrite vague task descriptions into more precise annotation instructions.