NVIDIA Nemotron Nano 2: An Accurate and Efficient Hybrid Mamba-Transformer Reasoning Model

We introduce Nemotron-Nano-9B-v2, a hybrid Mamba-Transformer language model designed to increase throughput for reasoning workloads while achieving state-of-the-art accuracy compared to similarly-sized models. Nemotron-Nano-9B-v2 builds on the Nemotron-H architecture, in which the majority of the self-attention layers in the common Transformer architecture are replaced with Mamba-2 layers, to achieve improved inference speed when generating the long thinking traces needed for reasoning. We create Nemotron-Nano-9B-v2 by first pre-training a 12-billion-parameter model (Nemotron-Nano-12B-v2-Base) on 20 trillion tokens using an FP8 training recipe. After aligning Nemotron-Nano-12B-v2-Base, we employ the Minitron strategy to compress and distill the model with the goal of enabling inference on up to 128k tokens on a single NVIDIA A10G GPU (22GiB of memory, bfloat16 precision). Compared to existing similarly-sized models (e.g., Qwen3-8B), we show that Nemotron-Nano-9B-v2 achieves on-par or better accuracy on reasoning benchmarks while achieving up to 6x higher inference throughput in reasoning settings like 8k input and 16k output tokens. We are releasing Nemotron-Nano-9B-v2, Nemotron-Nano12B-v2-Base, and Nemotron-Nano-9B-v2-Base checkpoints along with the majority of our pre- and post-training datasets on Hugging Face.

Power Stabilization for AI Training Datacenters

Large Artificial Intelligence (AI) training workloads spanning several tens of thousands of GPUs present unique power management challenges. These arise due to the high variability in power consumption during the training. Given the synchronous nature of these jobs, during every iteration there is a computation-heavy phase, where each GPU works on the local data, and a communication-heavy phase where all the GPUs synchronize on the data. Because compute-heavy phases require much more power than communication phases, large power swings occur. The amplitude of these power swings is ever increasing with the increase in the size of training jobs. An even bigger challenge arises from the frequency spectrum of these power swings which, if harmonized with critical frequencies of utilities, can cause physical damage to the power grid infrastructure. Therefore, to continue scaling AI training workloads safely, we need to stabilize the power of such workloads. This paper introduces the challenge with production data and explores innovative solutions across the stack: software, GPU hardware, and datacenter infrastructure. We present the pros and cons of each of these approaches and finally present a multi-pronged approach to solving the challenge. The proposed solutions are rigorously tested using a combination of real hardware and Microsoft's in-house cloud power simulator, providing critical insights into the efficacy of these interventions under real-world conditions.

Pseudo-Asynchronous Local SGD: Robust and Efficient Data-Parallel Training

Following AI scaling trends, frontier models continue to grow in size and continue to be trained on larger datasets. Training these models requires huge investments in exascale computational resources, which has in turn driven development of distributed deep learning methods. Data parallelism is an essential approach to speed up training, but it requires frequent global communication between workers, which can bottleneck training at the largest scales. In this work, we propose a method called Pseudo-Asynchronous Local SGD (PALSGD) to improve the efficiency of data-parallel training. PALSGD is an extension of Local SGD (Stich, 2018) and DiLoCo (Douillard et al., 2023), designed to further reduce communication frequency by introducing a pseudo-synchronization mechanism. PALSGD allows the use of longer synchronization intervals compared to standard Local SGD. Despite the reduced communication frequency, the pseudo-synchronization approach ensures that model consistency is maintained, leading to performance results comparable to those achieved with more frequent synchronization. Furthermore, we provide a theoretical analysis of PALSGD, establishing its convergence and deriving its convergence rate. This analysis offers insights into the algorithm's behavior and performance guarantees. We evaluated PALSGD on image classification and language modeling tasks. Our results show that PALSGD achieves better performance in less time compared to existing methods like Distributed Data Parallel (DDP), and DiLoCo. Notably, PALSGD trains 18.4% faster than DDP on ImageNet-1K with ResNet-50, 24.4% faster than DDP on TinyStories with GPT-Neo125M, and 21.1% faster than DDP on TinyStories with GPT-Neo-8M.

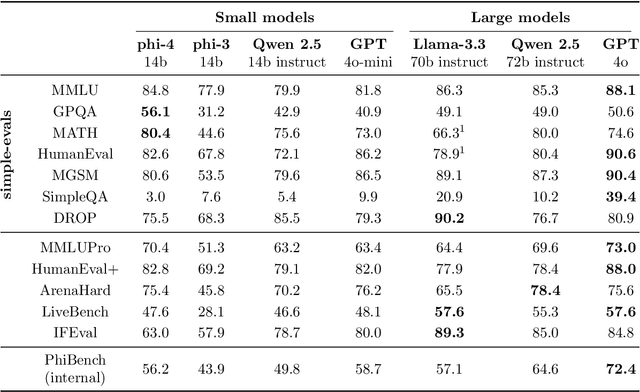
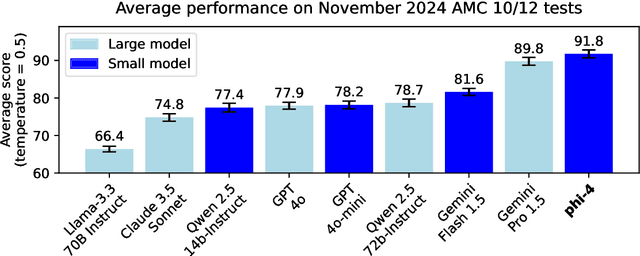
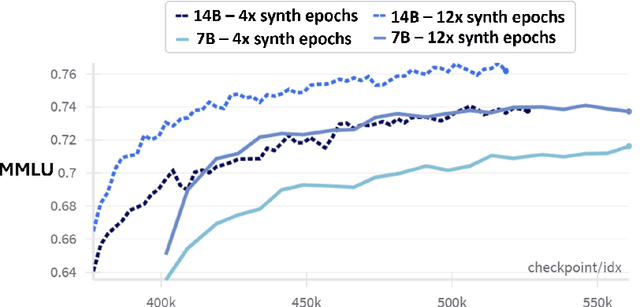
Phi-4 Technical Report

We present phi-4, a 14-billion parameter language model developed with a training recipe that is centrally focused on data quality. Unlike most language models, where pre-training is based primarily on organic data sources such as web content or code, phi-4 strategically incorporates synthetic data throughout the training process. While previous models in the Phi family largely distill the capabilities of a teacher model (specifically GPT-4), phi-4 substantially surpasses its teacher model on STEM-focused QA capabilities, giving evidence that our data-generation and post-training techniques go beyond distillation. Despite minimal changes to the phi-3 architecture, phi-4 achieves strong performance relative to its size -- especially on reasoning-focused benchmarks -- due to improved data, training curriculum, and innovations in the post-training scheme.

Phi-3 Technical Report: A Highly Capable Language Model Locally on Your Phone

We introduce phi-3-mini, a 3.8 billion parameter language model trained on 3.3 trillion tokens, whose overall performance, as measured by both academic benchmarks and internal testing, rivals that of models such as Mixtral 8x7B and GPT-3.5 (e.g., phi-3-mini achieves 69% on MMLU and 8.38 on MT-bench), despite being small enough to be deployed on a phone. The innovation lies entirely in our dataset for training, a scaled-up version of the one used for phi-2, composed of heavily filtered web data and synthetic data. The model is also further aligned for robustness, safety, and chat format. We also provide some initial parameter-scaling results with a 7B and 14B models trained for 4.8T tokens, called phi-3-small and phi-3-medium, both significantly more capable than phi-3-mini (e.g., respectively 75% and 78% on MMLU, and 8.7 and 8.9 on MT-bench).

SciAI4Industry -- Solving PDEs for industry-scale problems with deep learning

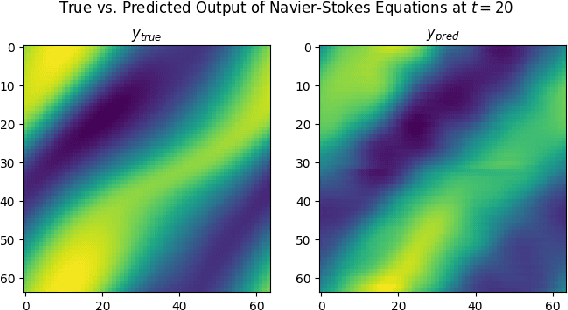
Solving partial differential equations with deep learning makes it possible to reduce simulation times by multiple orders of magnitude and unlock scientific methods that typically rely on large numbers of sequential simulations, such as optimization and uncertainty quantification. Two of the largest challenges of adopting scientific AI for industrial problem settings is that training datasets must be simulated in advance and that neural networks for solving large-scale PDEs exceed the memory capabilities of current GPUs. We introduce a distributed programming API in the Julia language for simulating training data in parallel on the cloud and without requiring users to manage the underlying HPC infrastructure. In addition, we show that model-parallel deep learning based on domain decomposition allows us to scale neural networks for solving PDEs to commercial-scale problem settings and achieve above 90% parallel efficiency. Combining our cloud API for training data generation and model-parallel deep learning, we train large-scale neural networks for solving the 3D Navier-Stokes equation and simulating 3D CO2 flow in porous media. For the CO2 example, we simulate a training dataset based on a commercial carbon capture and storage (CCS) project and train a neural network for CO2 flow simulation on a 3D grid with over 2 million cells that is 5 orders of magnitudes faster than a conventional numerical simulator and 3,200 times cheaper.

Towards Large-Scale Learned Solvers for Parametric PDEs with Model-Parallel Fourier Neural Operators

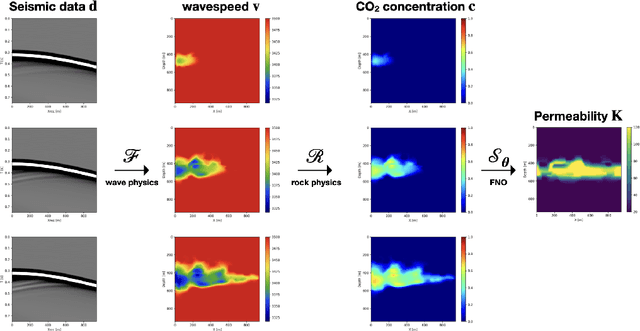
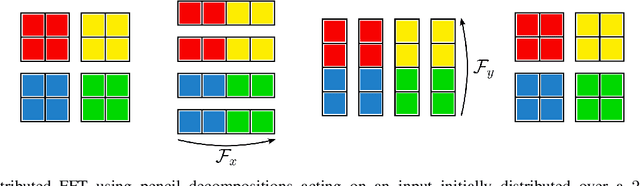
Fourier neural operators (FNOs) are a recently introduced neural network architecture for learning solution operators of partial differential equations (PDEs), which have been shown to perform significantly better than comparable approaches based on convolutional networks. Once trained, FNOs can achieve speed-ups of multiple orders of magnitude over conventional numerical PDE solvers. However, due to the high dimensionality of their input data and network weights, FNOs have so far only been applied to two-dimensional or small three-dimensional problems. To remove this limited problem-size barrier, we propose a model-parallel version of FNOs based on domain-decomposition of both the input data and network weights. We demonstrate that our model-parallel FNO is able to predict time-varying PDE solutions of over 3.2 billions variables on Summit using up to 768 GPUs and show an example of training a distributed FNO on the Azure cloud for simulating multiphase CO$_2$ dynamics in the Earth's subsurface.

A Linear Algebraic Approach to Model Parallelism in Deep Learning

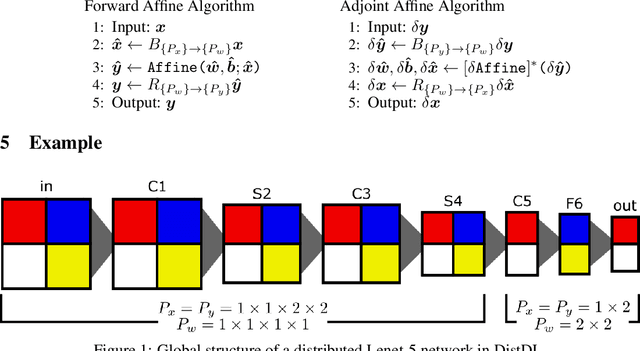
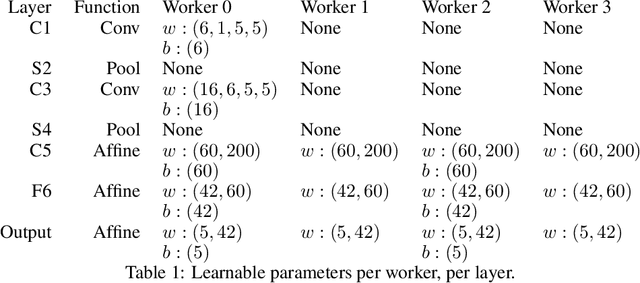
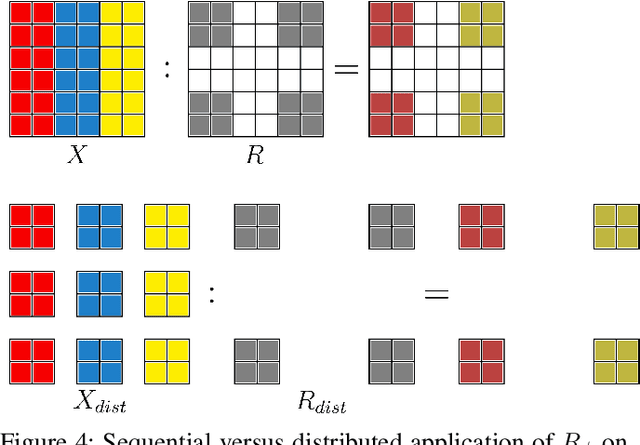
Training deep neural networks (DNNs) in large-cluster computing environments is increasingly necessary, as networks grow in size and complexity. Local memory and processing limitations require robust data and model parallelism for crossing compute node boundaries. We propose a linear-algebraic approach to model parallelism in deep learning, which allows parallel distribution of any tensor in the DNN. Rather than rely on automatic differentiation tools, which do not universally support distributed memory parallelism models, we show that parallel data movement operations, e.g., broadcast, sum-reduce, and halo exchange, are linear operators, and by defining the relevant spaces and inner products, we manually develop the adjoint, or backward, operators required for gradient-based training of DNNs. We build distributed DNN layers using these parallel primitives, composed with sequential layer implementations, and demonstrate their application by building and training a distributed DNN using DistDL, a PyTorch and MPI-based distributed deep learning toolkit.