On the Emergence of Thinking in LLMs I: Searching for the Right Intuition

Recent AI advancements, such as OpenAI's new models, are transforming LLMs into LRMs (Large Reasoning Models) that perform reasoning during inference, taking extra time and compute for higher-quality outputs. We aim to uncover the algorithmic framework for training LRMs. Methods like self-consistency, PRM, and AlphaZero suggest reasoning as guided search. We ask: what is the simplest, most scalable way to enable search in LLMs? We propose a post-training framework called Reinforcement Learning via Self-Play (RLSP). RLSP involves three steps: (1) supervised fine-tuning with human or synthetic demonstrations of the reasoning process, (2) using an exploration reward signal to encourage diverse and efficient reasoning behaviors, and (3) RL training with an outcome verifier to ensure correctness while preventing reward hacking. Our key innovation is to decouple exploration and correctness signals during PPO training, carefully balancing them to improve performance and efficiency. Empirical studies in the math domain show that RLSP improves reasoning. On the Llama-3.1-8B-Instruct model, RLSP can boost performance by 23% in MATH-500 test set; On AIME 2024 math problems, Qwen2.5-32B-Instruct improved by 10% due to RLSP. However, a more important finding of this work is that the models trained using RLSP, even with the simplest exploration reward that encourages the model to take more intermediate steps, showed several emergent behaviors such as backtracking, exploration of ideas, and verification. These findings demonstrate that RLSP framework might be enough to enable emergence of complex reasoning abilities in LLMs when scaled. Lastly, we propose a theory as to why RLSP search strategy is more suitable for LLMs inspired by a remarkable result that says CoT provably increases computational power of LLMs, which grows as the number of steps in CoT \cite{li2024chain,merrill2023expresssive}.

DiscQuant: A Quantization Method for Neural Networks Inspired by Discrepancy Theory

Quantizing the weights of a neural network has two steps: (1) Finding a good low bit-complexity representation for weights (which we call the quantization grid) and (2) Rounding the original weights to values in the quantization grid. In this paper, we study the problem of rounding optimally given any quantization grid. The simplest and most commonly used way to round is Round-to-Nearest (RTN). By rounding in a data-dependent way instead, one can improve the quality of the quantized model significantly. We study the rounding problem from the lens of \emph{discrepancy theory}, which studies how well we can round a continuous solution to a discrete solution without affecting solution quality too much. We prove that given $m=\mathrm{poly}(1/\epsilon)$ samples from the data distribution, we can round all but $O(m)$ model weights such that the expected approximation error of the quantized model on the true data distribution is $\le \epsilon$ as long as the space of gradients of the original model is approximately low rank (which we empirically validate). Our proof, which is algorithmic, inspired a simple and practical rounding algorithm called \emph{DiscQuant}. In our experiments, we demonstrate that DiscQuant significantly improves over the prior state-of-the-art rounding method called GPTQ and the baseline RTN over a range of benchmarks on Phi3mini-3.8B and Llama3.1-8B. For example, rounding Phi3mini-3.8B to a fixed quantization grid with 3.25 bits per parameter using DiscQuant gets 64\% accuracy on the GSM8k dataset, whereas GPTQ achieves 54\% and RTN achieves 31\% (the original model achieves 84\%). We make our code available at https://github.com/jerry-chee/DiscQuant.

Differentially Private Synthetic Data via Foundation Model APIs 2: Text

Text data has become extremely valuable due to the emergence of machine learning algorithms that learn from it. A lot of high-quality text data generated in the real world is private and therefore cannot be shared or used freely due to privacy concerns. Generating synthetic replicas of private text data with a formal privacy guarantee, i.e., differential privacy (DP), offers a promising and scalable solution. However, existing methods necessitate DP finetuning of large language models (LLMs) on private data to generate DP synthetic data. This approach is not viable for proprietary LLMs (e.g., GPT-3.5) and also demands considerable computational resources for open-source LLMs. Lin et al. (2024) recently introduced the Private Evolution (PE) algorithm to generate DP synthetic images with only API access to diffusion models. In this work, we propose an augmented PE algorithm, named Aug-PE, that applies to the complex setting of text. We use API access to an LLM and generate DP synthetic text without any model training. We conduct comprehensive experiments on three benchmark datasets. Our results demonstrate that Aug-PE produces DP synthetic text that yields competitive utility with the SOTA DP finetuning baselines. This underscores the feasibility of relying solely on API access of LLMs to produce high-quality DP synthetic texts, thereby facilitating more accessible routes to privacy-preserving LLM applications. Our code and data are available at https://github.com/AI-secure/aug-pe.

Privacy-Preserving In-Context Learning with Differentially Private Few-Shot Generation

We study the problem of in-context learning (ICL) with large language models (LLMs) on private datasets. This scenario poses privacy risks, as LLMs may leak or regurgitate the private examples demonstrated in the prompt. We propose a novel algorithm that generates synthetic few-shot demonstrations from the private dataset with formal differential privacy (DP) guarantees, and show empirically that it can achieve effective ICL. We conduct extensive experiments on standard benchmarks and compare our algorithm with non-private ICL and zero-shot solutions. Our results demonstrate that our algorithm can achieve competitive performance with strong privacy levels. These results open up new possibilities for ICL with privacy protection for a broad range of applications.

Textbooks Are All You Need

We introduce phi-1, a new large language model for code, with significantly smaller size than competing models: phi-1 is a Transformer-based model with 1.3B parameters, trained for 4 days on 8 A100s, using a selection of ``textbook quality" data from the web (6B tokens) and synthetically generated textbooks and exercises with GPT-3.5 (1B tokens). Despite this small scale, phi-1 attains pass@1 accuracy 50.6% on HumanEval and 55.5% on MBPP. It also displays surprising emergent properties compared to phi-1-base, our model before our finetuning stage on a dataset of coding exercises, and phi-1-small, a smaller model with 350M parameters trained with the same pipeline as phi-1 that still achieves 45% on HumanEval.

Differentially Private Synthetic Data via Foundation Model APIs 1: Images

Generating differentially private (DP) synthetic data that closely resembles the original private data without leaking sensitive user information is a scalable way to mitigate privacy concerns in the current data-driven world. In contrast to current practices that train customized models for this task, we aim to generate DP Synthetic Data via APIs (DPSDA), where we treat foundation models as blackboxes and only utilize their inference APIs. Such API-based, training-free approaches are easier to deploy as exemplified by the recent surge in the number of API-based apps. These approaches can also leverage the power of large foundation models which are accessible via their inference APIs while the model weights are unreleased. However, this comes with greater challenges due to strictly more restrictive model access and the additional need to protect privacy from the API provider. In this paper, we present a new framework called Private Evolution (PE) to solve this problem and show its initial promise on synthetic images. Surprisingly, PE can match or even outperform state-of-the-art (SOTA) methods without any model training. For example, on CIFAR10 (with ImageNet as the public data), we achieve FID<=7.9 with privacy cost epsilon=0.67, significantly improving the previous SOTA from epsilon=32. We further demonstrate the promise of applying PE on large foundation models such as Stable Diffusion to tackle challenging private datasets with a small number of high-resolution images.

Selective Pre-training for Private Fine-tuning

Suppose we want to train text prediction models in email clients or word processors. The models must preserve the privacy of user data and adhere to a specific fixed size to meet memory and inference time requirements. We introduce a generic framework to solve this problem. Specifically, we are given a public dataset $D_\text{pub}$ and a private dataset $D_\text{priv}$ corresponding to a downstream task $T$. How should we pre-train a fixed-size model $M$ on $D_\text{pub}$ and fine-tune it on $D_\text{priv}$ such that performance of $M$ with respect to $T$ is maximized and $M$ satisfies differential privacy with respect to $D_\text{priv}$? We show that pre-training on a {\em subset} of dataset $D_\text{pub}$ that brings the public distribution closer to the private distribution is a crucial ingredient to maximize the transfer learning abilities of $M$ after pre-training, especially in the regimes where model sizes are relatively small. Besides performance improvements, our framework also shows that with careful pre-training and private fine-tuning, {\em smaller models} can match the performance of much larger models, highlighting the promise of differentially private training as a tool for model compression and efficiency.

Algorithmic Aspects of the Log-Laplace Transform and a Non-Euclidean Proximal Sampler

The development of efficient sampling algorithms catering to non-Euclidean geometries has been a challenging endeavor, as discretization techniques which succeed in the Euclidean setting do not readily carry over to more general settings. We develop a non-Euclidean analog of the recent proximal sampler of [LST21], which naturally induces regularization by an object known as the log-Laplace transform (LLT) of a density. We prove new mathematical properties (with an algorithmic flavor) of the LLT, such as strong convexity-smoothness duality and an isoperimetric inequality, which are used to prove a mixing time on our proximal sampler matching [LST21] under a warm start. As our main application, we show our warm-started sampler improves the value oracle complexity of differentially private convex optimization in $\ell_p$ and Schatten-$p$ norms for $p \in [1, 2]$ to match the Euclidean setting [GLL22], while retaining state-of-the-art excess risk bounds [GLLST23]. We find our investigation of the LLT to be a promising proof-of-concept of its utility as a tool for designing samplers, and outline directions for future exploration.

Private Convex Optimization in General Norms

We propose a new framework for differentially private optimization of convex functions which are Lipschitz in an arbitrary norm $\normx{\cdot}$. Our algorithms are based on a regularized exponential mechanism which samples from the density $\propto \exp(-k(F+\mu r))$ where $F$ is the empirical loss and $r$ is a regularizer which is strongly convex with respect to $\normx{\cdot}$, generalizing a recent work of \cite{GLL22} to non-Euclidean settings. We show that this mechanism satisfies Gaussian differential privacy and solves both DP-ERM (empirical risk minimization) and DP-SCO (stochastic convex optimization), by using localization tools from convex geometry. Our framework is the first to apply to private convex optimization in general normed spaces, and directly recovers non-private SCO rates achieved by mirror descent, as the privacy parameter $\eps \to \infty$. As applications, for Lipschitz optimization in $\ell_p$ norms for all $p \in (1, 2)$, we obtain the first optimal privacy-utility tradeoffs; for $p = 1$, we improve tradeoffs obtained by the recent works \cite{AsiFKT21, BassilyGN21} by at least a logarithmic factor. Our $\ell_p$ norm and Schatten-$p$ norm optimization frameworks are complemented with polynomial-time samplers whose query complexity we explicitly bound.

Private Convex Optimization via Exponential Mechanism

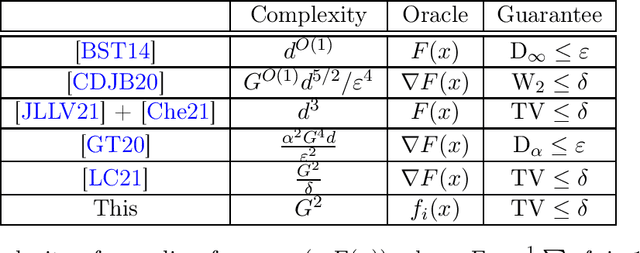
In this paper, we study private optimization problems for non-smooth convex functions $F(x)=\mathbb{E}_i f_i(x)$ on $\mathbb{R}^d$. We show that modifying the exponential mechanism by adding an $\ell_2^2$ regularizer to $F(x)$ and sampling from $\pi(x)\propto \exp(-k(F(x)+\mu\|x\|_2^2/2))$ recovers both the known optimal empirical risk and population loss under $(\epsilon,\delta)$-DP. Furthermore, we show how to implement this mechanism using $\widetilde{O}(n \min(d, n))$ queries to $f_i(x)$ for the DP-SCO where $n$ is the number of samples/users and $d$ is the ambient dimension. We also give a (nearly) matching lower bound $\widetilde{\Omega}(n \min(d, n))$ on the number of evaluation queries. Our results utilize the following tools that are of independent interest: (1) We prove Gaussian Differential Privacy (GDP) of the exponential mechanism if the loss function is strongly convex and the perturbation is Lipschitz. Our privacy bound is \emph{optimal} as it includes the privacy of Gaussian mechanism as a special case and is proved using the isoperimetric inequality for strongly log-concave measures. (2) We show how to sample from $\exp(-F(x)-\mu \|x\|^2_2/2)$ for $G$-Lipschitz $F$ with $\eta$ error in total variation (TV) distance using $\widetilde{O}((G^2/\mu) \log^2(d/\eta))$ unbiased queries to $F(x)$. This is the first sampler whose query complexity has \emph{polylogarithmic dependence} on both dimension $d$ and accuracy $\eta$.