Learned multiphysics inversion with differentiable programming and machine learning

We present the Seismic Laboratory for Imaging and Modeling/Monitoring (SLIM) open-source software framework for computational geophysics and, more generally, inverse problems involving the wave-equation (e.g., seismic and medical ultrasound), regularization with learned priors, and learned neural surrogates for multiphase flow simulations. By integrating multiple layers of abstraction, our software is designed to be both readable and scalable. This allows researchers to easily formulate their problems in an abstract fashion while exploiting the latest developments in high-performance computing. We illustrate and demonstrate our design principles and their benefits by means of building a scalable prototype for permeability inversion from time-lapse crosswell seismic data, which aside from coupling of wave physics and multiphase flow, involves machine learning.

SciAI4Industry -- Solving PDEs for industry-scale problems with deep learning

Solving partial differential equations with deep learning makes it possible to reduce simulation times by multiple orders of magnitude and unlock scientific methods that typically rely on large numbers of sequential simulations, such as optimization and uncertainty quantification. Two of the largest challenges of adopting scientific AI for industrial problem settings is that training datasets must be simulated in advance and that neural networks for solving large-scale PDEs exceed the memory capabilities of current GPUs. We introduce a distributed programming API in the Julia language for simulating training data in parallel on the cloud and without requiring users to manage the underlying HPC infrastructure. In addition, we show that model-parallel deep learning based on domain decomposition allows us to scale neural networks for solving PDEs to commercial-scale problem settings and achieve above 90% parallel efficiency. Combining our cloud API for training data generation and model-parallel deep learning, we train large-scale neural networks for solving the 3D Navier-Stokes equation and simulating 3D CO2 flow in porous media. For the CO2 example, we simulate a training dataset based on a commercial carbon capture and storage (CCS) project and train a neural network for CO2 flow simulation on a 3D grid with over 2 million cells that is 5 orders of magnitudes faster than a conventional numerical simulator and 3,200 times cheaper.

Towards Large-Scale Learned Solvers for Parametric PDEs with Model-Parallel Fourier Neural Operators

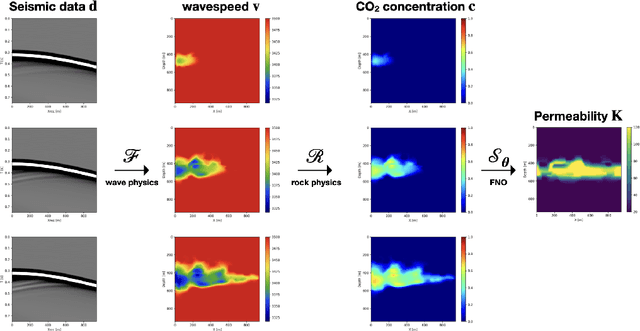
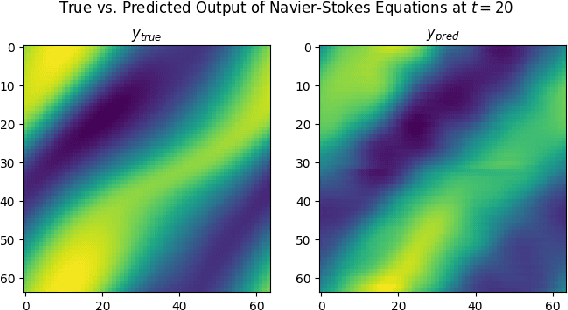
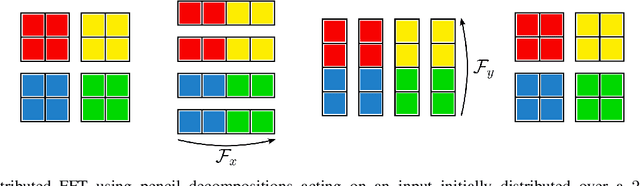
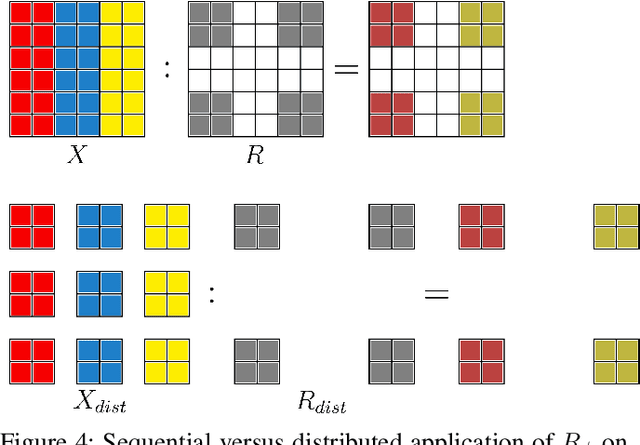
Fourier neural operators (FNOs) are a recently introduced neural network architecture for learning solution operators of partial differential equations (PDEs), which have been shown to perform significantly better than comparable approaches based on convolutional networks. Once trained, FNOs can achieve speed-ups of multiple orders of magnitude over conventional numerical PDE solvers. However, due to the high dimensionality of their input data and network weights, FNOs have so far only been applied to two-dimensional or small three-dimensional problems. To remove this limited problem-size barrier, we propose a model-parallel version of FNOs based on domain-decomposition of both the input data and network weights. We demonstrate that our model-parallel FNO is able to predict time-varying PDE solutions of over 3.2 billions variables on Summit using up to 768 GPUs and show an example of training a distributed FNO on the Azure cloud for simulating multiphase CO$_2$ dynamics in the Earth's subsurface.

Preconditioned training of normalizing flows for variational inference in inverse problems

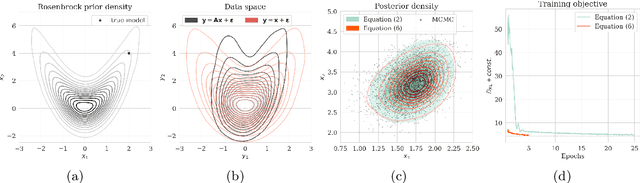
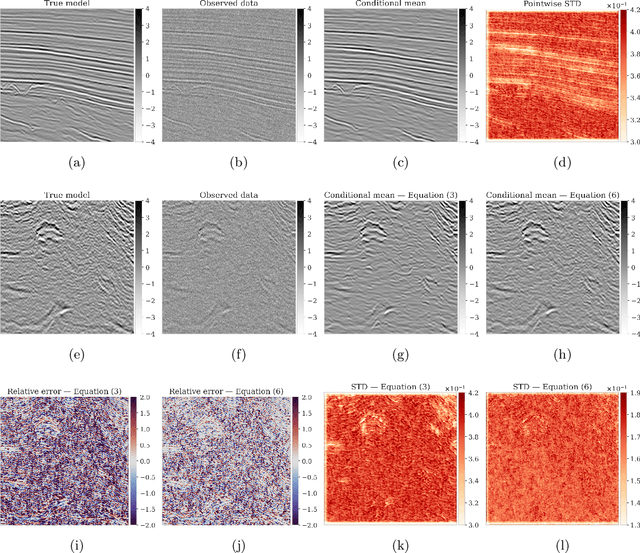
Obtaining samples from the posterior distribution of inverse problems with expensive forward operators is challenging especially when the unknowns involve the strongly heterogeneous Earth. To meet these challenges, we propose a preconditioning scheme involving a conditional normalizing flow (NF) capable of sampling from a low-fidelity posterior distribution directly. This conditional NF is used to speed up the training of the high-fidelity objective involving minimization of the Kullback-Leibler divergence between the predicted and the desired high-fidelity posterior density for indirect measurements at hand. To minimize costs associated with the forward operator, we initialize the high-fidelity NF with the weights of the pretrained low-fidelity NF, which is trained beforehand on available model and data pairs. Our numerical experiments, including a 2D toy and a seismic compressed sensing example, demonstrate that thanks to the preconditioning considerable speed-ups are achievable compared to training NFs from scratch.

Faster Uncertainty Quantification for Inverse Problems with Conditional Normalizing Flows

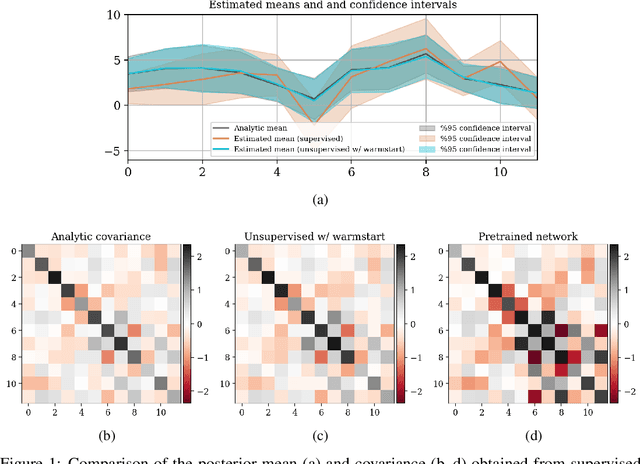
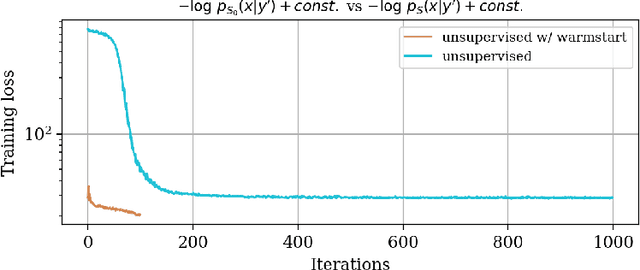
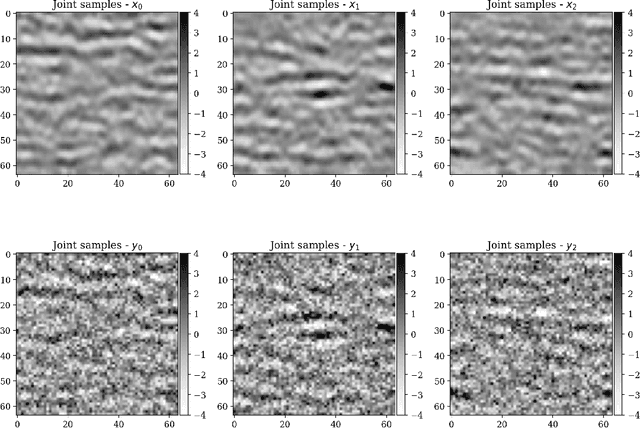
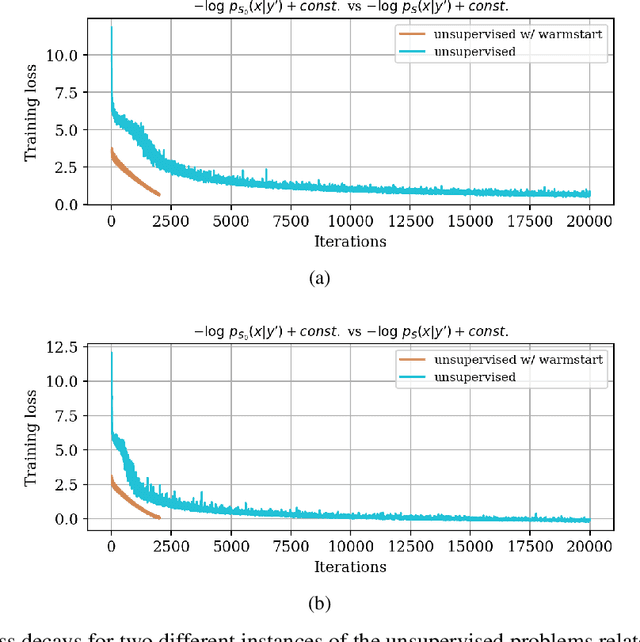
In inverse problems, we often have access to data consisting of paired samples $(x,y)\sim p_{X,Y}(x,y)$ where $y$ are partial observations of a physical system, and $x$ represents the unknowns of the problem. Under these circumstances, we can employ supervised training to learn a solution $x$ and its uncertainty from the observations $y$. We refer to this problem as the "supervised" case. However, the data $y\sim p_{Y}(y)$ collected at one point could be distributed differently than observations $y'\sim p_{Y}'(y')$, relevant for a current set of problems. In the context of Bayesian inference, we propose a two-step scheme, which makes use of normalizing flows and joint data to train a conditional generator $q_{\theta}(x|y)$ to approximate the target posterior density $p_{X|Y}(x|y)$. Additionally, this preliminary phase provides a density function $q_{\theta}(x|y)$, which can be recast as a prior for the "unsupervised" problem, e.g.~when only the observations $y'\sim p_{Y}'(y')$, a likelihood model $y'|x$, and a prior on $x'$ are known. We then train another invertible generator with output density $q'_{\phi}(x|y')$ specifically for $y'$, allowing us to sample from the posterior $p_{X|Y}'(x|y')$. We present some synthetic results that demonstrate considerable training speedup when reusing the pretrained network $q_{\theta}(x|y')$ as a warm start or preconditioning for approximating $p_{X|Y}'(x|y')$, instead of learning from scratch. This training modality can be interpreted as an instance of transfer learning. This result is particularly relevant for large-scale inverse problems that employ expensive numerical simulations.

Parameterizing uncertainty by deep invertible networks, an application to reservoir characterization

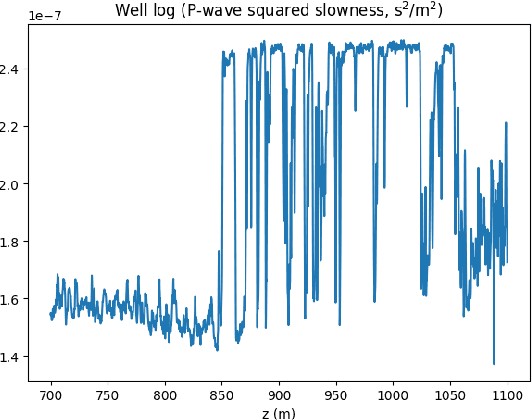
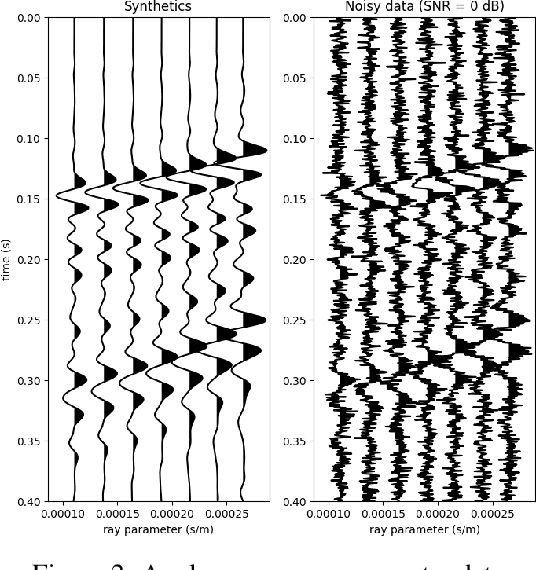
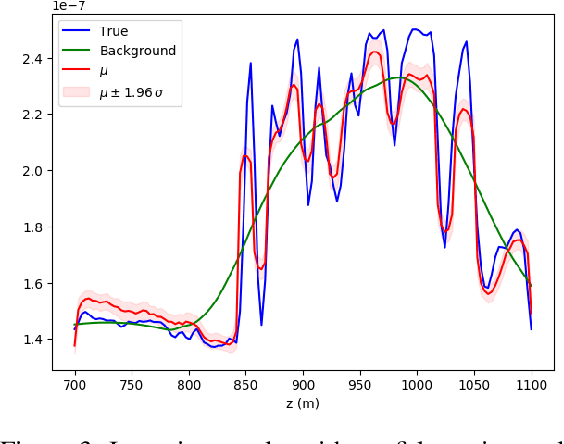
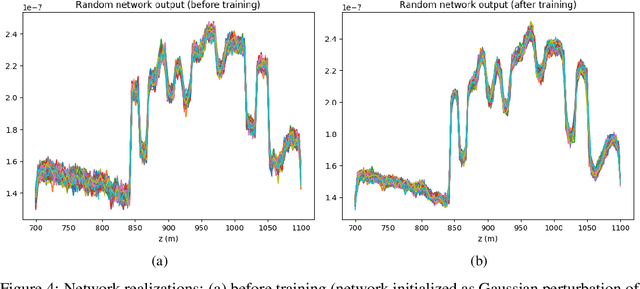
Uncertainty quantification for full-waveform inversion provides a probabilistic characterization of the ill-conditioning of the problem, comprising the sensitivity of the solution with respect to the starting model and data noise. This analysis allows to assess the confidence in the candidate solution and how it is reflected in the tasks that are typically performed after imaging (e.g., stratigraphic segmentation following reservoir characterization). Classically, uncertainty comes in the form of a probability distribution formulated from Bayesian principles, from which we seek to obtain samples. A popular solution involves Monte Carlo sampling. Here, we propose instead an approach characterized by training a deep network that "pushes forward" Gaussian random inputs into the model space (representing, for example, density or velocity) as if they were sampled from the actual posterior distribution. Such network is designed to solve a variational optimization problem based on the Kullback-Leibler divergence between the posterior and the network output distributions. This work is fundamentally rooted in recent developments for invertible networks. Special invertible architectures, besides being computational advantageous with respect to traditional networks, do also enable analytic computation of the output density function. Therefore, after training, these networks can be readily used as a new prior for a related inversion problem. This stands in stark contrast with Monte-Carlo methods, which only produce samples. We validate these ideas with an application to angle-versus-ray parameter analysis for reservoir characterization.