Efficiently Computing Similarities to Private Datasets

Many methods in differentially private model training rely on computing the similarity between a query point (such as public or synthetic data) and private data. We abstract out this common subroutine and study the following fundamental algorithmic problem: Given a similarity function $f$ and a large high-dimensional private dataset $X \subset \mathbb{R}^d$, output a differentially private (DP) data structure which approximates $\sum_{x \in X} f(x,y)$ for any query $y$. We consider the cases where $f$ is a kernel function, such as $f(x,y) = e^{-\|x-y\|_2^2/\sigma^2}$ (also known as DP kernel density estimation), or a distance function such as $f(x,y) = \|x-y\|_2$, among others. Our theoretical results improve upon prior work and give better privacy-utility trade-offs as well as faster query times for a wide range of kernels and distance functions. The unifying approach behind our results is leveraging `low-dimensional structures' present in the specific functions $f$ that we study, using tools such as provable dimensionality reduction, approximation theory, and one-dimensional decomposition of the functions. Our algorithms empirically exhibit improved query times and accuracy over prior state of the art. We also present an application to DP classification. Our experiments demonstrate that the simple methodology of classifying based on average similarity is orders of magnitude faster than prior DP-SGD based approaches for comparable accuracy.

Differentially Private Synthetic Data via Foundation Model APIs 2: Text

Text data has become extremely valuable due to the emergence of machine learning algorithms that learn from it. A lot of high-quality text data generated in the real world is private and therefore cannot be shared or used freely due to privacy concerns. Generating synthetic replicas of private text data with a formal privacy guarantee, i.e., differential privacy (DP), offers a promising and scalable solution. However, existing methods necessitate DP finetuning of large language models (LLMs) on private data to generate DP synthetic data. This approach is not viable for proprietary LLMs (e.g., GPT-3.5) and also demands considerable computational resources for open-source LLMs. Lin et al. (2024) recently introduced the Private Evolution (PE) algorithm to generate DP synthetic images with only API access to diffusion models. In this work, we propose an augmented PE algorithm, named Aug-PE, that applies to the complex setting of text. We use API access to an LLM and generate DP synthetic text without any model training. We conduct comprehensive experiments on three benchmark datasets. Our results demonstrate that Aug-PE produces DP synthetic text that yields competitive utility with the SOTA DP finetuning baselines. This underscores the feasibility of relying solely on API access of LLMs to produce high-quality DP synthetic texts, thereby facilitating more accessible routes to privacy-preserving LLM applications. Our code and data are available at https://github.com/AI-secure/aug-pe.

Privately Aligning Language Models with Reinforcement Learning

Positioned between pre-training and user deployment, aligning large language models (LLMs) through reinforcement learning (RL) has emerged as a prevailing strategy for training instruction following-models such as ChatGPT. In this work, we initiate the study of privacy-preserving alignment of LLMs through Differential Privacy (DP) in conjunction with RL. Following the influential work of Ziegler et al. (2020), we study two dominant paradigms: (i) alignment via RL without human in the loop (e.g., positive review generation) and (ii) alignment via RL from human feedback (RLHF) (e.g., summarization in a human-preferred way). We give a new DP framework to achieve alignment via RL, and prove its correctness. Our experimental results validate the effectiveness of our approach, offering competitive utility while ensuring strong privacy protections.

Exploring the Limits of Differentially Private Deep Learning with Group-wise Clipping

Differentially private deep learning has recently witnessed advances in computational efficiency and privacy-utility trade-off. We explore whether further improvements along the two axes are possible and provide affirmative answers leveraging two instantiations of \emph{group-wise clipping}. To reduce the compute time overhead of private learning, we show that \emph{per-layer clipping}, where the gradient of each neural network layer is clipped separately, allows clipping to be performed in conjunction with backpropagation in differentially private optimization. This results in private learning that is as memory-efficient and almost as fast per training update as non-private learning for many workflows of interest. While per-layer clipping with constant thresholds tends to underperform standard flat clipping, per-layer clipping with adaptive thresholds matches or outperforms flat clipping under given training epoch constraints, hence attaining similar or better task performance within less wall time. To explore the limits of scaling (pretrained) models in differentially private deep learning, we privately fine-tune the 175 billion-parameter GPT-3. We bypass scaling challenges associated with clipping gradients that are distributed across multiple devices with \emph{per-device clipping} that clips the gradient of each model piece separately on its host device. Privately fine-tuning GPT-3 with per-device clipping achieves a task performance at $\epsilon=1$ better than what is attainable by non-privately fine-tuning the largest GPT-2 on a summarization task.

Unveiling Transformers with LEGO: a synthetic reasoning task

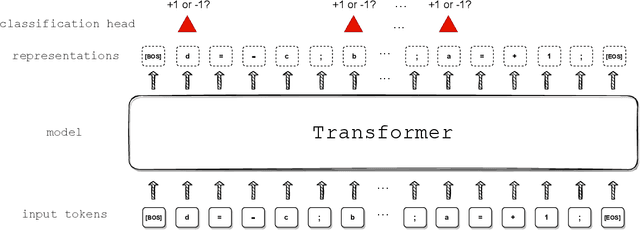
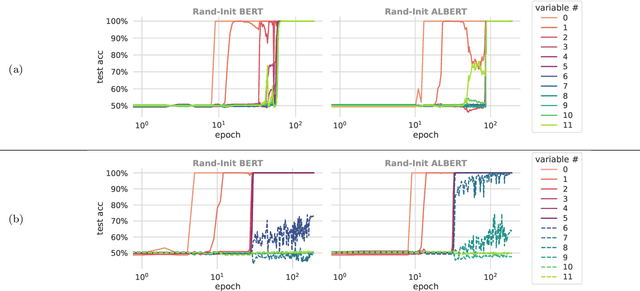
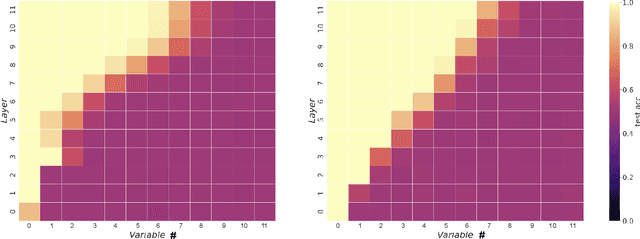
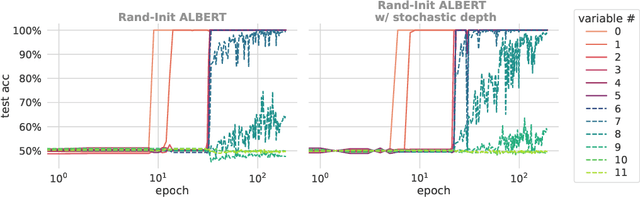
We propose a synthetic task, LEGO (Learning Equality and Group Operations), that encapsulates the problem of following a chain of reasoning, and we study how the transformer architecture learns this task. We pay special attention to data effects such as pretraining (on seemingly unrelated NLP tasks) and dataset composition (e.g., differing chain length at training and test time), as well as architectural variants such as weight-tied layers or adding convolutional components. We study how the trained models eventually succeed at the task, and in particular, we are able to understand (to some extent) some of the attention heads as well as how the information flows in the network. Based on these observations we propose a hypothesis that here pretraining helps merely due to being a smart initialization rather than some deep knowledge stored in the network. We also observe that in some data regime the trained transformer finds "shortcut" solutions to follow the chain of reasoning, which impedes the model's ability to generalize to simple variants of the main task, and moreover we find that one can prevent such shortcut with appropriate architecture modification or careful data preparation. Motivated by our findings, we begin to explore the task of learning to execute C programs, where a convolutional modification to transformers, namely adding convolutional structures in the key/query/value maps, shows an encouraging edge.

Differentially Private Model Compression

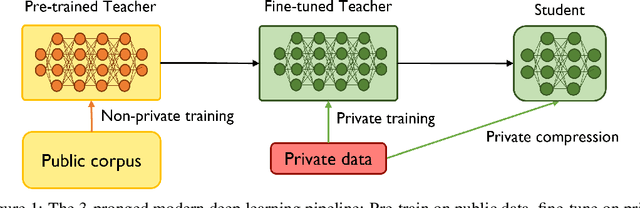
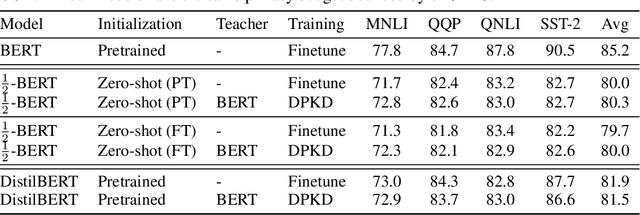
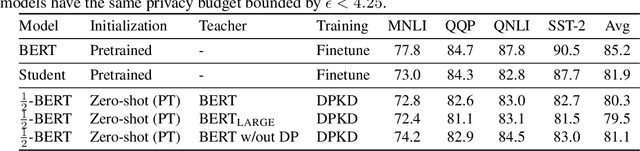
Recent papers have shown that large pre-trained language models (LLMs) such as BERT, GPT-2 can be fine-tuned on private data to achieve performance comparable to non-private models for many downstream Natural Language Processing (NLP) tasks while simultaneously guaranteeing differential privacy. The inference cost of these models -- which consist of hundreds of millions of parameters -- however, can be prohibitively large. Hence, often in practice, LLMs are compressed before they are deployed in specific applications. In this paper, we initiate the study of differentially private model compression and propose frameworks for achieving 50% sparsity levels while maintaining nearly full performance. We demonstrate these ideas on standard GLUE benchmarks using BERT models, setting benchmarks for future research on this topic.

Differentially Private Fine-tuning of Language Models

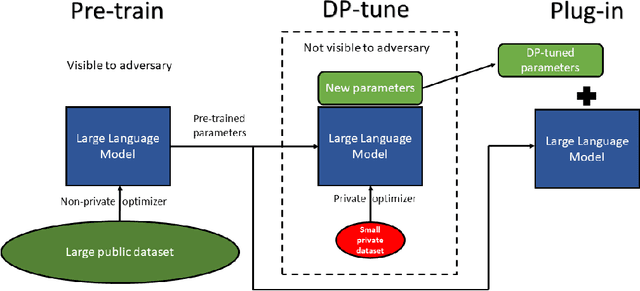
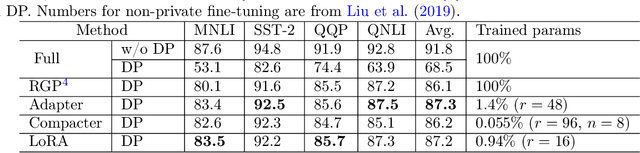
We give simpler, sparser, and faster algorithms for differentially private fine-tuning of large-scale pre-trained language models, which achieve the state-of-the-art privacy versus utility tradeoffs on many standard NLP tasks. We propose a meta-framework for this problem, inspired by the recent success of highly parameter-efficient methods for fine-tuning. Our experiments show that differentially private adaptations of these approaches outperform previous private algorithms in three important dimensions: utility, privacy, and the computational and memory cost of private training. On many commonly studied datasets, the utility of private models approaches that of non-private models. For example, on the MNLI dataset we achieve an accuracy of $87.8\%$ using RoBERTa-Large and $83.5\%$ using RoBERTa-Base with a privacy budget of $\epsilon = 6.7$. In comparison, absent privacy constraints, RoBERTa-Large achieves an accuracy of $90.2\%$. Our findings are similar for natural language generation tasks. Privately fine-tuning with DART, GPT-2-Small, GPT-2-Medium, GPT-2-Large, and GPT-2-XL achieve BLEU scores of 38.5, 42.0, 43.1, and 43.8 respectively (privacy budget of $\epsilon = 6.8,\delta=$ 1e-5) whereas the non-private baseline is $48.1$. All our experiments suggest that larger models are better suited for private fine-tuning: while they are well known to achieve superior accuracy non-privately, we find that they also better maintain their accuracy when privacy is introduced.

Faster Kernel Matrix Algebra via Density Estimation

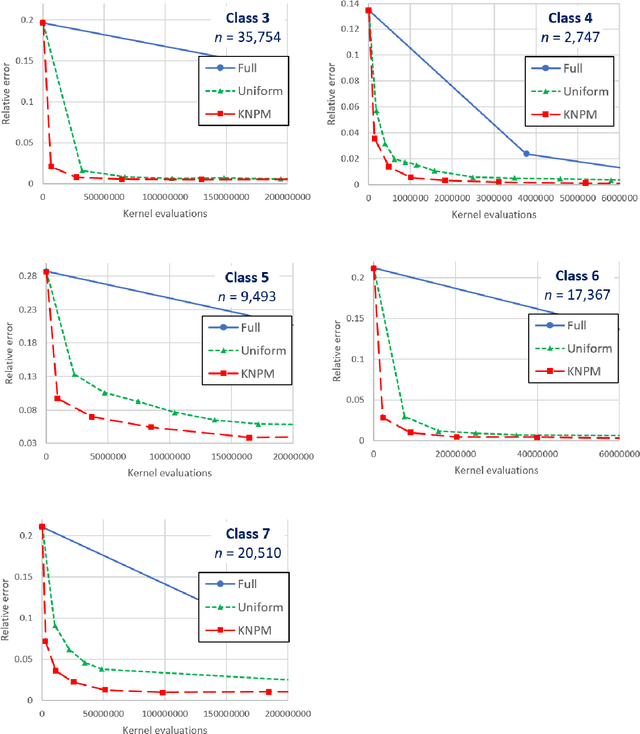
We study fast algorithms for computing fundamental properties of a positive semidefinite kernel matrix $K \in \mathbb{R}^{n \times n}$ corresponding to $n$ points $x_1,\ldots,x_n \in \mathbb{R}^d$. In particular, we consider estimating the sum of kernel matrix entries, along with its top eigenvalue and eigenvector. We show that the sum of matrix entries can be estimated to $1+\epsilon$ relative error in time $sublinear$ in $n$ and linear in $d$ for many popular kernels, including the Gaussian, exponential, and rational quadratic kernels. For these kernels, we also show that the top eigenvalue (and an approximate eigenvector) can be approximated to $1+\epsilon$ relative error in time $subquadratic$ in $n$ and linear in $d$. Our algorithms represent significant advances in the best known runtimes for these problems. They leverage the positive definiteness of the kernel matrix, along with a recent line of work on efficient kernel density estimation.

Generating (Formulaic) Text by Splicing Together Nearest Neighbors

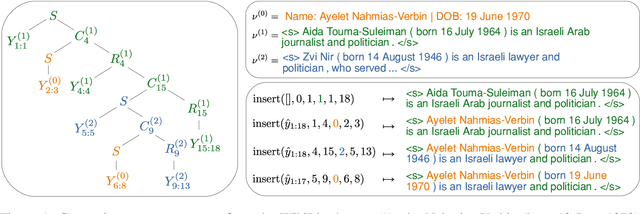
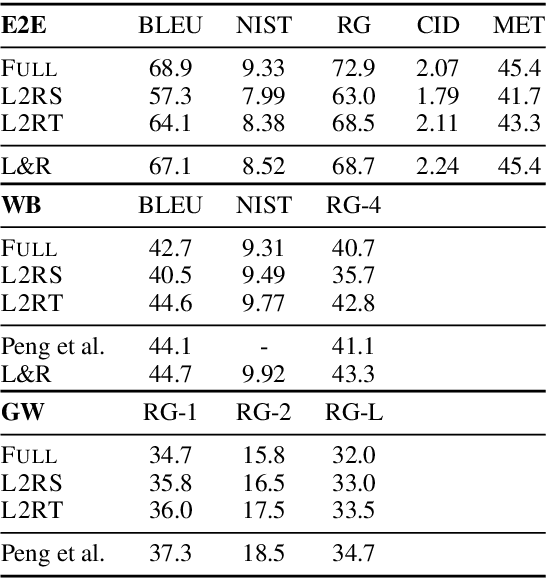
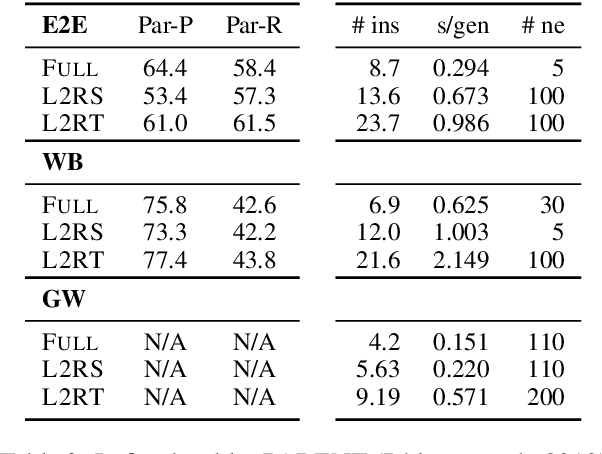
We propose to tackle conditional text generation tasks, especially those which require generating formulaic text, by splicing together segments of text from retrieved "neighbor" source-target pairs. Unlike recent work that conditions on retrieved neighbors in an encoder-decoder setting but generates text token-by-token, left-to-right, we learn a policy that directly manipulates segments of neighbor text (i.e., by inserting or replacing them) to form an output. Standard techniques for training such a policy require an oracle derivation for each generation, and we prove that finding the shortest such derivation can be reduced to parsing under a particular weighted context-free grammar. We find that policies learned in this way allow for interpretable table-to-text or headline generation that is competitive with neighbor-based token-level policies on automatic metrics, though on all but one dataset neighbor-based policies underperform a strong neighborless baseline. In all cases, however, generating by splicing is faster.

Impossibility Results for Grammar-Compressed Linear Algebra

To handle vast amounts of data, it is natural and popular to compress vectors and matrices. When we compress a vector from size $N$ down to size $n \ll N$, it certainly makes it easier to store and transmit efficiently, but does it also make it easier to process? In this paper we consider lossless compression schemes, and ask if we can run our computations on the compressed data as efficiently as if the original data was that small. That is, if an operation has time complexity $T(\rm{inputsize})$, can we perform it on the compressed representation in time $T(n)$ rather than $T(N)$? We consider the most basic linear algebra operations: inner product, matrix-vector multiplication, and matrix multiplication. In particular, given two compressed vectors, can we compute their inner product in time $O(n)$? Or perhaps we must decompress first and then multiply, spending $\Omega(N)$ time? The answer depends on the compression scheme. While for simple ones such as Run-Length-Encoding (RLE) the inner product can be done in $O(n)$ time, we prove that this is impossible for compressions from a richer class: essentially $n^2$ or even larger runtimes are needed in the worst case (under complexity assumptions). This is the class of grammar-compressions containing most popular methods such as the Lempel-Ziv family. These schemes are more compressing than the simple RLE, but alas, we prove that performing computations on them is much harder.