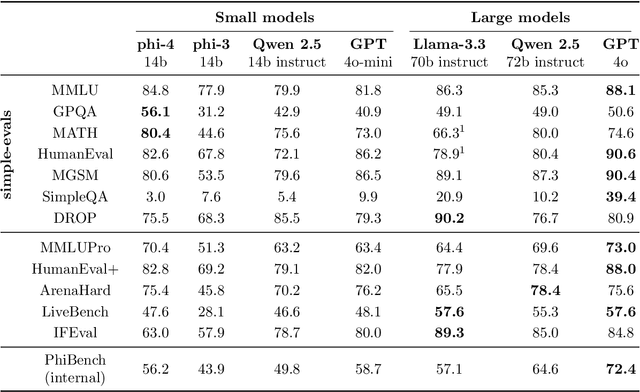
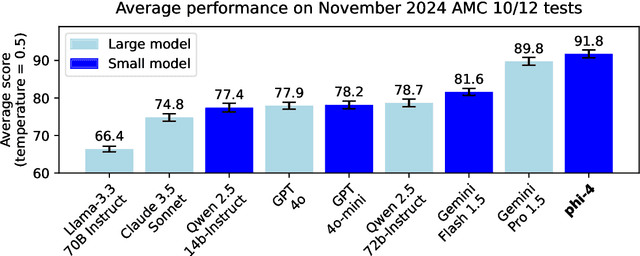
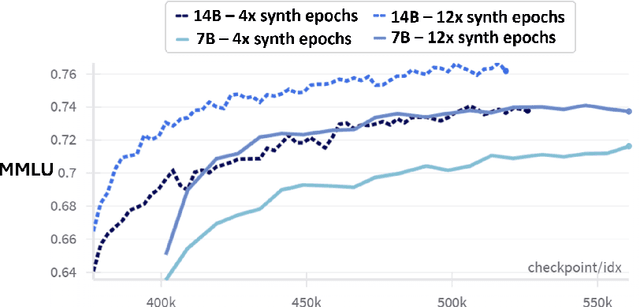
Phi-4 Technical Report

We present phi-4, a 14-billion parameter language model developed with a training recipe that is centrally focused on data quality. Unlike most language models, where pre-training is based primarily on organic data sources such as web content or code, phi-4 strategically incorporates synthetic data throughout the training process. While previous models in the Phi family largely distill the capabilities of a teacher model (specifically GPT-4), phi-4 substantially surpasses its teacher model on STEM-focused QA capabilities, giving evidence that our data-generation and post-training techniques go beyond distillation. Despite minimal changes to the phi-3 architecture, phi-4 achieves strong performance relative to its size -- especially on reasoning-focused benchmarks -- due to improved data, training curriculum, and innovations in the post-training scheme.

Phi-3 Technical Report: A Highly Capable Language Model Locally on Your Phone

We introduce phi-3-mini, a 3.8 billion parameter language model trained on 3.3 trillion tokens, whose overall performance, as measured by both academic benchmarks and internal testing, rivals that of models such as Mixtral 8x7B and GPT-3.5 (e.g., phi-3-mini achieves 69% on MMLU and 8.38 on MT-bench), despite being small enough to be deployed on a phone. The innovation lies entirely in our dataset for training, a scaled-up version of the one used for phi-2, composed of heavily filtered web data and synthetic data. The model is also further aligned for robustness, safety, and chat format. We also provide some initial parameter-scaling results with a 7B and 14B models trained for 4.8T tokens, called phi-3-small and phi-3-medium, both significantly more capable than phi-3-mini (e.g., respectively 75% and 78% on MMLU, and 8.7 and 8.9 on MT-bench).

Great, Now Write an Article About That: The Crescendo Multi-Turn LLM Jailbreak Attack

Large Language Models (LLMs) have risen significantly in popularity and are increasingly being adopted across multiple applications. These LLMs are heavily aligned to resist engaging in illegal or unethical topics as a means to avoid contributing to responsible AI harms. However, a recent line of attacks, known as "jailbreaks", seek to overcome this alignment. Intuitively, jailbreak attacks aim to narrow the gap between what the model can do and what it is willing to do. In this paper, we introduce a novel jailbreak attack called Crescendo. Unlike existing jailbreak methods, Crescendo is a multi-turn jailbreak that interacts with the model in a seemingly benign manner. It begins with a general prompt or question about the task at hand and then gradually escalates the dialogue by referencing the model's replies, progressively leading to a successful jailbreak. We evaluate Crescendo on various public systems, including ChatGPT, Gemini Pro, Gemini-Ultra, LlaMA-2 70b Chat, and Anthropic Chat. Our results demonstrate the strong efficacy of Crescendo, with it achieving high attack success rates across all evaluated models and tasks. Furthermore, we introduce Crescendomation, a tool that automates the Crescendo attack, and our evaluation showcases its effectiveness against state-of-the-art models.

TinyGSM: achieving >80% on GSM8k with small language models

Small-scale models offer various computational advantages, and yet to which extent size is critical for problem-solving abilities remains an open question. Specifically for solving grade school math, the smallest model size so far required to break the 80\% barrier on the GSM8K benchmark remains to be 34B. Our work studies how high-quality datasets may be the key for small language models to acquire mathematical reasoning. We introduce \texttt{TinyGSM}, a synthetic dataset of 12.3M grade school math problems paired with Python solutions, generated fully by GPT-3.5. After finetuning on \texttt{TinyGSM}, we find that a duo of a 1.3B generation model and a 1.3B verifier model can achieve 81.5\% accuracy, outperforming existing models that are orders of magnitude larger. This also rivals the performance of the GPT-3.5 ``teacher'' model (77.4\%), from which our model's training data is generated. Our approach is simple and has two key components: 1) the high-quality dataset \texttt{TinyGSM}, 2) the use of a verifier, which selects the final outputs from multiple candidate generations.

Positional Description Matters for Transformers Arithmetic

Transformers, central to the successes in modern Natural Language Processing, often falter on arithmetic tasks despite their vast capabilities --which paradoxically include remarkable coding abilities. We observe that a crucial challenge is their naive reliance on positional information to solve arithmetic problems with a small number of digits, leading to poor performance on larger numbers. Herein, we delve deeper into the role of positional encoding, and propose several ways to fix the issue, either by modifying the positional encoding directly, or by modifying the representation of the arithmetic task to leverage standard positional encoding differently. We investigate the value of these modifications for three tasks: (i) classical multiplication, (ii) length extrapolation in addition, and (iii) addition in natural language context. For (i) we train a small model on a small dataset (100M parameters and 300k samples) with remarkable aptitude in (direct, no scratchpad) 15 digits multiplication and essentially perfect up to 12 digits, while usual training in this context would give a model failing at 4 digits multiplication. In the experiments on addition, we use a mere 120k samples to demonstrate: for (ii) extrapolation from 10 digits to testing on 12 digits numbers while usual training would have no extrapolation, and for (iii) almost perfect accuracy up to 5 digits while usual training would be correct only up to 3 digits (which is essentially memorization with a training set of 120k samples).

Who's Harry Potter? Approximate Unlearning in LLMs

Large language models (LLMs) are trained on massive internet corpora that often contain copyrighted content. This poses legal and ethical challenges for the developers and users of these models, as well as the original authors and publishers. In this paper, we propose a novel technique for unlearning a subset of the training data from a LLM, without having to retrain it from scratch. We evaluate our technique on the task of unlearning the Harry Potter books from the Llama2-7b model (a generative language model recently open-sourced by Meta). While the model took over 184K GPU-hours to pretrain, we show that in about 1 GPU hour of finetuning, we effectively erase the model's ability to generate or recall Harry Potter-related content, while its performance on common benchmarks (such as Winogrande, Hellaswag, arc, boolq and piqa) remains almost unaffected. We make our fine-tuned model publicly available on HuggingFace for community evaluation. To the best of our knowledge, this is the first paper to present an effective technique for unlearning in generative language models. Our technique consists of three main components: First, we use a reinforced model that is further trained on the target data to identify the tokens that are most related to the unlearning target, by comparing its logits with those of a baseline model. Second, we replace idiosyncratic expressions in the target data with generic counterparts, and leverage the model's own predictions to generate alternative labels for every token. These labels aim to approximate the next-token predictions of a model that has not been trained on the target data. Third, we finetune the model on these alternative labels, which effectively erases the original text from the model's memory whenever it is prompted with its context.

Textbooks Are All You Need II: phi-1.5 technical report

We continue the investigation into the power of smaller Transformer-based language models as initiated by \textbf{TinyStories} -- a 10 million parameter model that can produce coherent English -- and the follow-up work on \textbf{phi-1}, a 1.3 billion parameter model with Python coding performance close to the state-of-the-art. The latter work proposed to use existing Large Language Models (LLMs) to generate ``textbook quality" data as a way to enhance the learning process compared to traditional web data. We follow the ``Textbooks Are All You Need" approach, focusing this time on common sense reasoning in natural language, and create a new 1.3 billion parameter model named \textbf{phi-1.5}, with performance on natural language tasks comparable to models 5x larger, and surpassing most non-frontier LLMs on more complex reasoning tasks such as grade-school mathematics and basic coding. More generally, \textbf{phi-1.5} exhibits many of the traits of much larger LLMs, both good -- such as the ability to ``think step by step" or perform some rudimentary in-context learning -- and bad, including hallucinations and the potential for toxic and biased generations -- encouragingly though, we are seeing improvement on that front thanks to the absence of web data. We open-source \textbf{phi-1.5} to promote further research on these urgent topics.

Textbooks Are All You Need

We introduce phi-1, a new large language model for code, with significantly smaller size than competing models: phi-1 is a Transformer-based model with 1.3B parameters, trained for 4 days on 8 A100s, using a selection of ``textbook quality" data from the web (6B tokens) and synthetically generated textbooks and exercises with GPT-3.5 (1B tokens). Despite this small scale, phi-1 attains pass@1 accuracy 50.6% on HumanEval and 55.5% on MBPP. It also displays surprising emergent properties compared to phi-1-base, our model before our finetuning stage on a dataset of coding exercises, and phi-1-small, a smaller model with 350M parameters trained with the same pipeline as phi-1 that still achieves 45% on HumanEval.

TinyStories: How Small Can Language Models Be and Still Speak Coherent English?

Language models (LMs) are powerful tools for natural language processing, but they often struggle to produce coherent and fluent text when they are small. Models with around 125M parameters such as GPT-Neo (small) or GPT-2 (small) can rarely generate coherent and consistent English text beyond a few words even after extensive training. This raises the question of whether the emergence of the ability to produce coherent English text only occurs at larger scales (with hundreds of millions of parameters or more) and complex architectures (with many layers of global attention). In this work, we introduce TinyStories, a synthetic dataset of short stories that only contain words that a typical 3 to 4-year-olds usually understand, generated by GPT-3.5 and GPT-4. We show that TinyStories can be used to train and evaluate LMs that are much smaller than the state-of-the-art models (below 10 million total parameters), or have much simpler architectures (with only one transformer block), yet still produce fluent and consistent stories with several paragraphs that are diverse and have almost perfect grammar, and demonstrate reasoning capabilities. We also introduce a new paradigm for the evaluation of language models: We suggest a framework which uses GPT-4 to grade the content generated by these models as if those were stories written by students and graded by a (human) teacher. This new paradigm overcomes the flaws of standard benchmarks which often requires the model's output to be very structures, and moreover provides a multidimensional score for the model, providing scores for different capabilities such as grammar, creativity and consistency. We hope that TinyStories can facilitate the development, analysis and research of LMs, especially for low-resource or specialized domains, and shed light on the emergence of language capabilities in LMs.

Sparks of Artificial General Intelligence: Early experiments with GPT-4

Artificial intelligence (AI) researchers have been developing and refining large language models (LLMs) that exhibit remarkable capabilities across a variety of domains and tasks, challenging our understanding of learning and cognition. The latest model developed by OpenAI, GPT-4, was trained using an unprecedented scale of compute and data. In this paper, we report on our investigation of an early version of GPT-4, when it was still in active development by OpenAI. We contend that (this early version of) GPT-4 is part of a new cohort of LLMs (along with ChatGPT and Google's PaLM for example) that exhibit more general intelligence than previous AI models. We discuss the rising capabilities and implications of these models. We demonstrate that, beyond its mastery of language, GPT-4 can solve novel and difficult tasks that span mathematics, coding, vision, medicine, law, psychology and more, without needing any special prompting. Moreover, in all of these tasks, GPT-4's performance is strikingly close to human-level performance, and often vastly surpasses prior models such as ChatGPT. Given the breadth and depth of GPT-4's capabilities, we believe that it could reasonably be viewed as an early (yet still incomplete) version of an artificial general intelligence (AGI) system. In our exploration of GPT-4, we put special emphasis on discovering its limitations, and we discuss the challenges ahead for advancing towards deeper and more comprehensive versions of AGI, including the possible need for pursuing a new paradigm that moves beyond next-word prediction. We conclude with reflections on societal influences of the recent technological leap and future research directions.