Muon is Provably Faster with Momentum Variance Reduction

Recent empirical research has demonstrated that deep learning optimizers based on the linear minimization oracle (LMO) over specifically chosen Non-Euclidean norm balls, such as Muon and Scion, outperform Adam-type methods in the training of large language models. In this work, we show that such optimizers can be provably improved by replacing their vanilla momentum by momentum variance reduction (MVR). Instead of proposing and analyzing MVR variants of Muon and Scion separately, we incorporate MVR into the recently proposed Gluon framework, which captures Muon, Scion and other specific Non-Euclidean LMO-based methods as special cases, and at the same time works with a more general smoothness assumption which better captures the layer-wise structure of neural networks. In the non-convex case, we incorporate MVR into Gluon in three different ways. All of them improve the convergence rate from ${\cal O} (\frac{1}{K^{1/4}})$ to ${\cal O} (\frac{1}{K^{1/3}})$. Additionally, we provide improved rates in the star-convex case. Finally, we conduct several numerical experiments that verify the superior performance of our proposed algorithms in terms of iteration complexity.

Enhancing XR Auditory Realism via Multimodal Scene-Aware Acoustic Rendering

In Extended Reality (XR), rendering sound that accurately simulates real-world acoustics is pivotal in creating lifelike and believable virtual experiences. However, existing XR spatial audio rendering methods often struggle with real-time adaptation to diverse physical scenes, causing a sensory mismatch between visual and auditory cues that disrupts user immersion. To address this, we introduce SAMOSA, a novel on-device system that renders spatially accurate sound by dynamically adapting to its physical environment. SAMOSA leverages a synergistic multimodal scene representation by fusing real-time estimations of room geometry, surface materials, and semantic-driven acoustic context. This rich representation then enables efficient acoustic calibration via scene priors, allowing the system to synthesize a highly realistic Room Impulse Response (RIR). We validate our system through technical evaluation using acoustic metrics for RIR synthesis across various room configurations and sound types, alongside an expert evaluation (N=12). Evaluation results demonstrate SAMOSA's feasibility and efficacy in enhancing XR auditory realism.

NoteIt: A System Converting Instructional Videos to Interactable Notes Through Multimodal Video Understanding

Users often take notes for instructional videos to access key knowledge later without revisiting long videos. Automated note generation tools enable users to obtain informative notes efficiently. However, notes generated by existing research or off-the-shelf tools fail to preserve the information conveyed in the original videos comprehensively, nor can they satisfy users' expectations for diverse presentation formats and interactive features when using notes digitally. In this work, we present NoteIt, a system, which automatically converts instructional videos to interactable notes using a novel pipeline that faithfully extracts hierarchical structure and multimodal key information from videos. With NoteIt's interface, users can interact with the system to further customize the content and presentation formats of the notes according to their preferences. We conducted both a technical evaluation and a comparison user study (N=36). The solid performance in objective metrics and the positive user feedback demonstrated the effectiveness of the pipeline and the overall usability of NoteIt. Project website: https://zhaorunning.github.io/NoteIt/

Thing2Reality: Transforming 2D Content into Conditioned Multiviews and 3D Gaussian Objects for XR Communication

During remote communication, participants often share both digital and physical content, such as product designs, digital assets, and environments, to enhance mutual understanding. Recent advances in augmented communication have facilitated users to swiftly create and share digital 2D copies of physical objects from video feeds into a shared space. However, conventional 2D representations of digital objects restricts users' ability to spatially reference items in a shared immersive environment. To address this, we propose Thing2Reality, an Extended Reality (XR) communication platform that enhances spontaneous discussions of both digital and physical items during remote sessions. With Thing2Reality, users can quickly materialize ideas or physical objects in immersive environments and share them as conditioned multiview renderings or 3D Gaussians. Thing2Reality enables users to interact with remote objects or discuss concepts in a collaborative manner. Our user study revealed that the ability to interact with and manipulate 3D representations of objects significantly enhances the efficiency of discussions, with the potential to augment discussion of 2D artifacts.

DocReLM: Mastering Document Retrieval with Language Model

With over 200 million published academic documents and millions of new documents being written each year, academic researchers face the challenge of searching for information within this vast corpus. However, existing retrieval systems struggle to understand the semantics and domain knowledge present in academic papers. In this work, we demonstrate that by utilizing large language models, a document retrieval system can achieve advanced semantic understanding capabilities, significantly outperforming existing systems. Our approach involves training the retriever and reranker using domain-specific data generated by large language models. Additionally, we utilize large language models to identify candidates from the references of retrieved papers to further enhance the performance. We use a test set annotated by academic researchers in the fields of quantum physics and computer vision to evaluate our system's performance. The results show that DocReLM achieves a Top 10 accuracy of 44.12% in computer vision, compared to Google Scholar's 15.69%, and an increase to 36.21% in quantum physics, while that of Google Scholar is 12.96%.

Communication-Efficient Distributed Learning with Local Immediate Error Compensation

Gradient compression with error compensation has attracted significant attention with the target of reducing the heavy communication overhead in distributed learning. However, existing compression methods either perform only unidirectional compression in one iteration with higher communication cost, or bidirectional compression with slower convergence rate. In this work, we propose the Local Immediate Error Compensated SGD (LIEC-SGD) optimization algorithm to break the above bottlenecks based on bidirectional compression and carefully designed compensation approaches. Specifically, the bidirectional compression technique is to reduce the communication cost, and the compensation technique compensates the local compression error to the model update immediately while only maintaining the global error variable on the server throughout the iterations to boost its efficacy. Theoretically, we prove that LIEC-SGD is superior to previous works in either the convergence rate or the communication cost, which indicates that LIEC-SGD could inherit the dual advantages from unidirectional compression and bidirectional compression. Finally, experiments of training deep neural networks validate the effectiveness of the proposed LIEC-SGD algorithm.

InstructPipe: Building Visual Programming Pipelines with Human Instructions

Visual programming provides beginner-level programmers with a coding-free experience to build their customized pipelines. Existing systems require users to build a pipeline entirely from scratch, implying that novice users need to set up and link appropriate nodes all by themselves, starting from a blank workspace. We present InstructPipe, an AI assistant that enables users to start prototyping machine learning (ML) pipelines with text instructions. We designed two LLM modules and a code interpreter to execute our solution. LLM modules generate pseudocode of a target pipeline, and the interpreter renders a pipeline in the node-graph editor for further human-AI collaboration. Technical evaluations reveal that InstructPipe reduces user interactions by 81.1% compared to traditional methods. Our user study (N=16) showed that InstructPipe empowers novice users to streamline their workflow in creating desired ML pipelines, reduce their learning curve, and spark innovative ideas with open-ended commands.

XAIR: A Framework of Explainable AI in Augmented Reality

Explainable AI (XAI) has established itself as an important component of AI-driven interactive systems. With Augmented Reality (AR) becoming more integrated in daily lives, the role of XAI also becomes essential in AR because end-users will frequently interact with intelligent services. However, it is unclear how to design effective XAI experiences for AR. We propose XAIR, a design framework that addresses "when", "what", and "how" to provide explanations of AI output in AR. The framework was based on a multi-disciplinary literature review of XAI and HCI research, a large-scale survey probing 500+ end-users' preferences for AR-based explanations, and three workshops with 12 experts collecting their insights about XAI design in AR. XAIR's utility and effectiveness was verified via a study with 10 designers and another study with 12 end-users. XAIR can provide guidelines for designers, inspiring them to identify new design opportunities and achieve effective XAI designs in AR.

Distributed Newton-Type Methods with Communication Compression and Bernoulli Aggregation

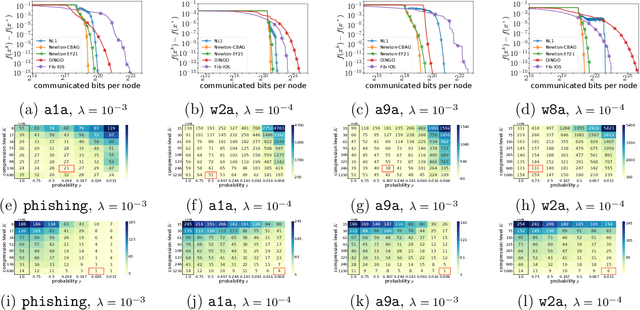
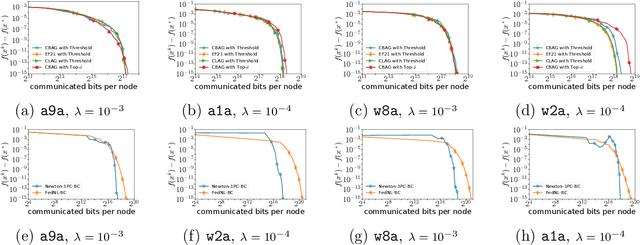
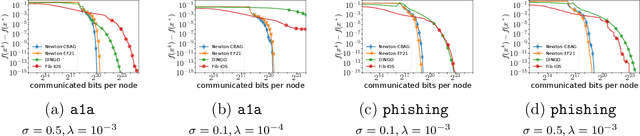
Despite their high computation and communication costs, Newton-type methods remain an appealing option for distributed training due to their robustness against ill-conditioned convex problems. In this work, we study ommunication compression and aggregation mechanisms for curvature information in order to reduce these costs while preserving theoretically superior local convergence guarantees. We prove that the recently developed class of three point compressors (3PC) of Richtarik et al. [2022] for gradient communication can be generalized to Hessian communication as well. This result opens up a wide variety of communication strategies, such as contractive compression} and lazy aggregation, available to our disposal to compress prohibitively costly curvature information. Moreover, we discovered several new 3PC mechanisms, such as adaptive thresholding and Bernoulli aggregation, which require reduced communication and occasional Hessian computations. Furthermore, we extend and analyze our approach to bidirectional communication compression and partial device participation setups to cater to the practical considerations of applications in federated learning. For all our methods, we derive fast condition-number-independent local linear and/or superlinear convergence rates. Finally, with extensive numerical evaluations on convex optimization problems, we illustrate that our designed schemes achieve state-of-the-art communication complexity compared to several key baselines using second-order information.

Basis Matters: Better Communication-Efficient Second Order Methods for Federated Learning

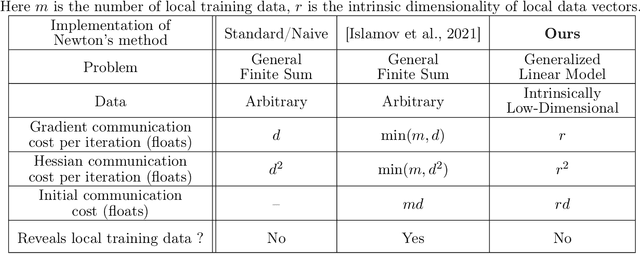
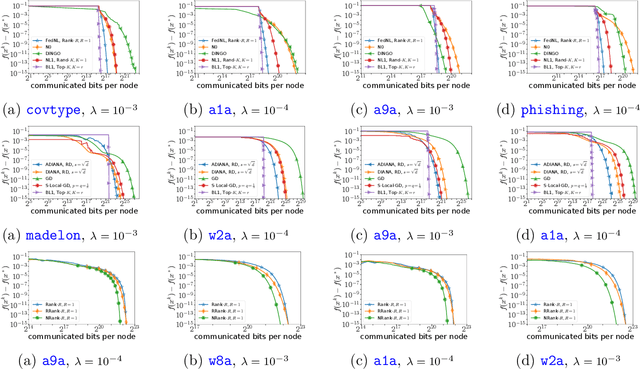
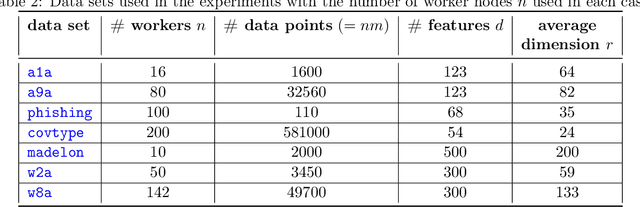
Recent advances in distributed optimization have shown that Newton-type methods with proper communication compression mechanisms can guarantee fast local rates and low communication cost compared to first order methods. We discover that the communication cost of these methods can be further reduced, sometimes dramatically so, with a surprisingly simple trick: {\em Basis Learn (BL)}. The idea is to transform the usual representation of the local Hessians via a change of basis in the space of matrices and apply compression tools to the new representation. To demonstrate the potential of using custom bases, we design a new Newton-type method (BL1), which reduces communication cost via both {\em BL} technique and bidirectional compression mechanism. Furthermore, we present two alternative extensions (BL2 and BL3) to partial participation to accommodate federated learning applications. We prove local linear and superlinear rates independent of the condition number. Finally, we support our claims with numerical experiments by comparing several first and second~order~methods.