Muon is Provably Faster with Momentum Variance Reduction

Recent empirical research has demonstrated that deep learning optimizers based on the linear minimization oracle (LMO) over specifically chosen Non-Euclidean norm balls, such as Muon and Scion, outperform Adam-type methods in the training of large language models. In this work, we show that such optimizers can be provably improved by replacing their vanilla momentum by momentum variance reduction (MVR). Instead of proposing and analyzing MVR variants of Muon and Scion separately, we incorporate MVR into the recently proposed Gluon framework, which captures Muon, Scion and other specific Non-Euclidean LMO-based methods as special cases, and at the same time works with a more general smoothness assumption which better captures the layer-wise structure of neural networks. In the non-convex case, we incorporate MVR into Gluon in three different ways. All of them improve the convergence rate from ${\cal O} (\frac{1}{K^{1/4}})$ to ${\cal O} (\frac{1}{K^{1/3}})$. Additionally, we provide improved rates in the star-convex case. Finally, we conduct several numerical experiments that verify the superior performance of our proposed algorithms in terms of iteration complexity.

Non-Euclidean SGD for Structured Optimization: Unified Analysis and Improved Rates

Recently, several instances of non-Euclidean SGD, including SignSGD, Lion, and Muon, have attracted significant interest from the optimization community due to their practical success in training deep neural networks. Consequently, a number of works have attempted to explain this success by developing theoretical convergence analyses. Unfortunately, these results cannot properly justify the superior performance of these methods, as they could not beat the convergence rate of vanilla Euclidean SGD. We resolve this important open problem by developing a new unified convergence analysis under the structured smoothness and gradient noise assumption. In particular, our results indicate that non-Euclidean SGD (i) can exploit the sparsity or low-rank structure of the upper bounds on the Hessian and gradient noise, (ii) can provably benefit from popular algorithmic tools such as extrapolation or momentum variance reduction, and (iii) can match the state-of-the-art convergence rates of adaptive and more complex optimization algorithms such as AdaGrad and Shampoo.

Understanding Gradient Orthogonalization for Deep Learning via Non-Euclidean Trust-Region Optimization

Optimization with matrix gradient orthogonalization has recently demonstrated impressive results in the training of deep neural networks (Jordan et al., 2024; Liu et al., 2025). In this paper, we provide a theoretical analysis of this approach. In particular, we show that the orthogonalized gradient method can be seen as a first-order trust-region optimization method, where the trust-region is defined in terms of the matrix spectral norm. Motivated by this observation, we provide the first theoretical analysis of the stochastic non-Euclidean trust-region gradient method with momentum, which recovers the Muon optimizer (Jordan et al., 2024) as a special case. In addition, we establish the convergence of the normalized SGD with momentum (Cutkosky and Mehta, 2020) in the constrained and composite setting, show that its iteration complexity of finding an $\varepsilon$-accurate solution can be improved from $\mathcal{O}(\varepsilon^{-3.5})$ to $\mathcal{O}(\varepsilon^{-3})$ under the star-convexity assumption, and obtain similar results for the Muon algorithm. Finally, our theoretical findings provide an explanation for the practical superiority of Muon compared to the Orthogonal-SGDM algorithm of Tuddenham et al. (2022).

On Linear Convergence in Smooth Convex-Concave Bilinearly-Coupled Saddle-Point Optimization: Lower Bounds and Optimal Algorithms

We revisit the smooth convex-concave bilinearly-coupled saddle-point problem of the form $\min_x\max_y f(x) + \langle y,\mathbf{B} x\rangle - g(y)$. In the highly specific case where each of the functions $f(x)$ and $g(y)$ is either affine or strongly convex, there exist lower bounds on the number of gradient evaluations and matrix-vector multiplications required to solve the problem, as well as matching optimal algorithms. A notable aspect of these algorithms is that they are able to attain linear convergence, i.e., the number of iterations required to solve the problem is proportional to $\log(1/\epsilon)$. However, the class of bilinearly-coupled saddle-point problems for which linear convergence is possible is much wider and can involve smooth non-strongly convex functions $f(x)$ and $g(y)$. Therefore, we develop the first lower complexity bounds and matching optimal linearly converging algorithms for this problem class. Our lower complexity bounds are much more general, but they cover and unify the existing results in the literature. On the other hand, our algorithm implements the separation of complexities, which, for the first time, enables the simultaneous achievement of both optimal gradient evaluation and matrix-vector multiplication complexities, resulting in the best theoretical performance to date.

An Optimal Algorithm for Strongly Convex Min-min Optimization

In this paper we study the smooth strongly convex minimization problem $\min_{x}\min_y f(x,y)$. The existing optimal first-order methods require $\mathcal{O}(\sqrt{\max\{\kappa_x,\kappa_y\}} \log 1/\epsilon)$ of computations of both $\nabla_x f(x,y)$ and $\nabla_y f(x,y)$, where $\kappa_x$ and $\kappa_y$ are condition numbers with respect to variable blocks $x$ and $y$. We propose a new algorithm that only requires $\mathcal{O}(\sqrt{\kappa_x} \log 1/\epsilon)$ of computations of $\nabla_x f(x,y)$ and $\mathcal{O}(\sqrt{\kappa_y} \log 1/\epsilon)$ computations of $\nabla_y f(x,y)$. In some applications $\kappa_x \gg \kappa_y$, and computation of $\nabla_y f(x,y)$ is significantly cheaper than computation of $\nabla_x f(x,y)$. In this case, our algorithm substantially outperforms the existing state-of-the-art methods.

Smooth Monotone Stochastic Variational Inequalities and Saddle Point Problems -- Survey

This paper is a survey of methods for solving smooth (strongly) monotone stochastic variational inequalities. To begin with, we give the deterministic foundation from which the stochastic methods eventually evolved. Then we review methods for the general stochastic formulation, and look at the finite sum setup. The last parts of the paper are devoted to various recent (not necessarily stochastic) advances in algorithms for variational inequalities.

Communication Acceleration of Local Gradient Methods via an Accelerated Primal-Dual Algorithm with Inexact Prox

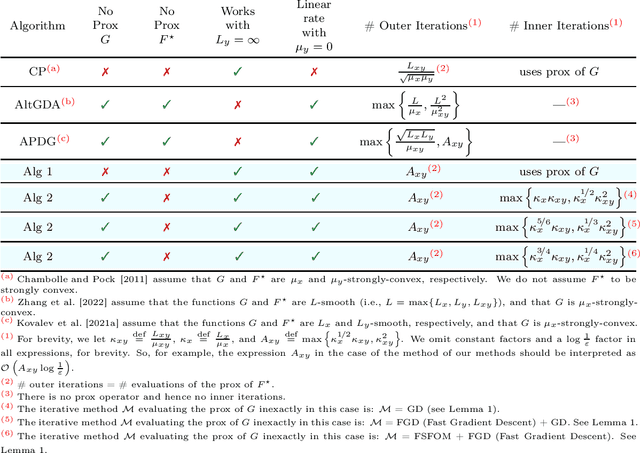
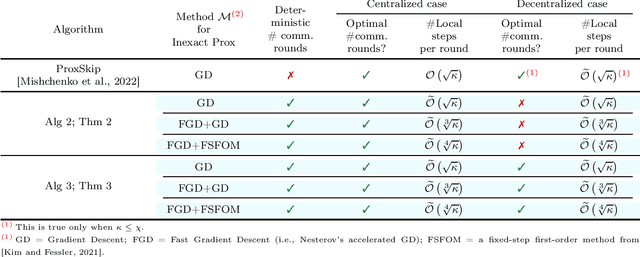
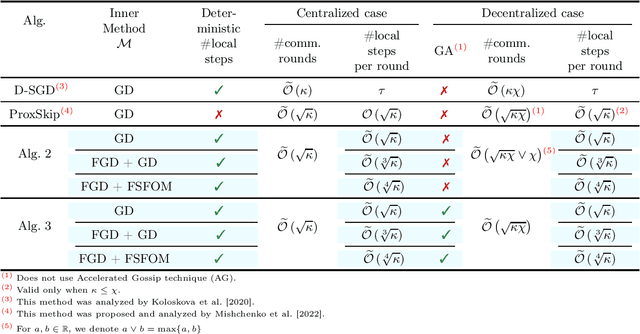
Inspired by a recent breakthrough of Mishchenko et al (2022), who for the first time showed that local gradient steps can lead to provable communication acceleration, we propose an alternative algorithm which obtains the same communication acceleration as their method (ProxSkip). Our approach is very different, however: it is based on the celebrated method of Chambolle and Pock (2011), with several nontrivial modifications: i) we allow for an inexact computation of the prox operator of a certain smooth strongly convex function via a suitable gradient-based method (e.g., GD, Fast GD or FSFOM), ii) we perform a careful modification of the dual update step in order to retain linear convergence. Our general results offer the new state-of-the-art rates for the class of strongly convex-concave saddle-point problems with bilinear coupling characterized by the absence of smoothness in the dual function. When applied to federated learning, we obtain a theoretically better alternative to ProxSkip: our method requires fewer local steps ($O(\kappa^{1/3})$ or $O(\kappa^{1/4})$, compared to $O(\kappa^{1/2})$ of ProxSkip), and performs a deterministic number of local steps instead. Like ProxSkip, our method can be applied to optimization over a connected network, and we obtain theoretical improvements here as well.

On Scaled Methods for Saddle Point Problems

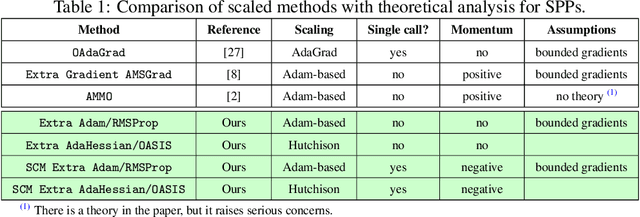
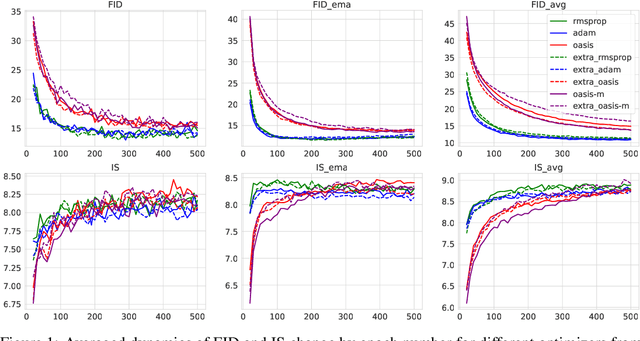
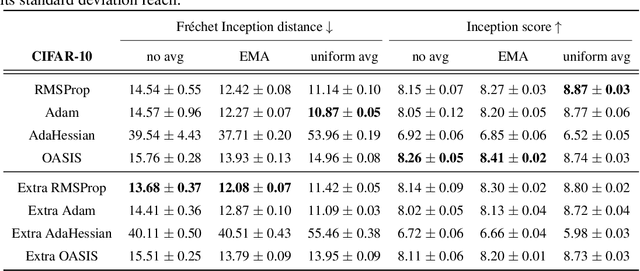
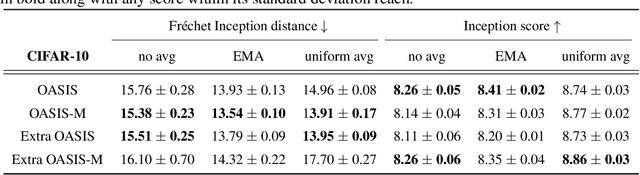
Methods with adaptive scaling of different features play a key role in solving saddle point problems, primarily due to Adam's popularity for solving adversarial machine learning problems, including GANS training. This paper carries out a theoretical analysis of the following scaling techniques for solving SPPs: the well-known Adam and RmsProp scaling and the newer AdaHessian and OASIS based on Hutchison approximation. We use the Extra Gradient and its improved version with negative momentum as the basic method. Experimental studies on GANs show good applicability not only for Adam, but also for other less popular methods.

Optimal Gradient Sliding and its Application to Distributed Optimization Under Similarity

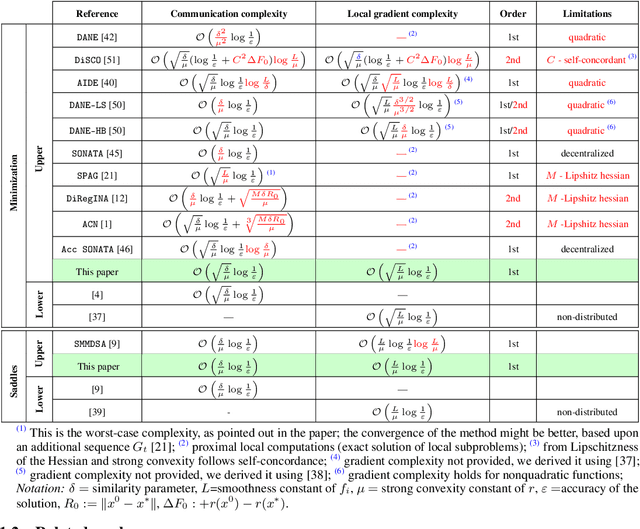
We study structured convex optimization problems, with additive objective $r:=p + q$, where $r$ is ($\mu$-strongly) convex, $q$ is $L_q$-smooth and convex, and $p$ is $L_p$-smooth, possibly nonconvex. For such a class of problems, we proposed an inexact accelerated gradient sliding method that can skip the gradient computation for one of these components while still achieving optimal complexity of gradient calls of $p$ and $q$, that is, $\mathcal{O}(\sqrt{L_p/\mu})$ and $\mathcal{O}(\sqrt{L_q/\mu})$, respectively. This result is much sharper than the classic black-box complexity $\mathcal{O}(\sqrt{(L_p+L_q)/\mu})$, especially when the difference between $L_q$ and $L_q$ is large. We then apply the proposed method to solve distributed optimization problems over master-worker architectures, under agents' function similarity, due to statistical data similarity or otherwise. The distributed algorithm achieves for the first time lower complexity bounds on {\it both} communication and local gradient calls, with the former having being a long-standing open problem. Finally the method is extended to distributed saddle-problems (under function similarity) by means of solving a class of variational inequalities, achieving lower communication and computation complexity bounds.

The First Optimal Acceleration of High-Order Methods in Smooth Convex Optimization

In this paper, we study the fundamental open question of finding the optimal high-order algorithm for solving smooth convex minimization problems. Arjevani et al. (2019) established the lower bound $\Omega\left(\epsilon^{-2/(3p+1)}\right)$ on the number of the $p$-th order oracle calls required by an algorithm to find an $\epsilon$-accurate solution to the problem, where the $p$-th order oracle stands for the computation of the objective function value and the derivatives up to the order $p$. However, the existing state-of-the-art high-order methods of Gasnikov et al. (2019b); Bubeck et al. (2019); Jiang et al. (2019) achieve the oracle complexity $\mathcal{O}\left(\epsilon^{-2/(3p+1)} \log (1/\epsilon)\right)$, which does not match the lower bound. The reason for this is that these algorithms require performing a complex binary search procedure, which makes them neither optimal nor practical. We fix this fundamental issue by providing the first algorithm with $\mathcal{O}\left(\epsilon^{-2/(3p+1)}\right)$ $p$-th order oracle complexity.