X-VFL: A New Vertical Federated Learning Framework with Cross Completion and Decision Subspace Alignment

Vertical Federated Learning (VFL) enables collaborative learning by integrating disjoint feature subsets from multiple clients/parties. However, VFL typically faces two key challenges: i) the requirement for perfectly aligned data samples across all clients (missing features are not allowed); ii) the requirement for joint collaborative inference/prediction involving all clients (it does not support locally independent inference on a single client). To address these challenges, we propose X-VFL, a new VFL framework designed to deal with the non-aligned data samples with (partially) missing features and to support locally independent inference of new data samples for each client. In particular, we design two novel modules in X-VFL: Cross Completion (XCom) and Decision Subspace Alignment (DS-Align). XCom can complete/reconstruct missing features for non-aligned data samples by leveraging information from other clients. DS-Align aligns local features with completed and global features across all clients within the decision subspace, thus enabling locally independent inference at each client. Moreover, we provide convergence theorems for different algorithms used in training X-VFL, showing an $O(1/\sqrt{T})$ convergence rate for SGD-type algorithms and an $O(1/T)$ rate for PAGE-type algorithms, where $T$ denotes the number of training update steps. Extensive experiments on real-world datasets demonstrate that X-VFL significantly outperforms existing methods, e.g., achieving a 15% improvement in accuracy on the image CIFAR-10 dataset and a 43% improvement on the medical MIMIC-III dataset. These results validate the practical effectiveness and superiority of X-VFL, particularly in scenarios involving partially missing features and locally independent inference.

Escaping Saddle Points in Heterogeneous Federated Learning via Distributed SGD with Communication Compression

We consider the problem of finding second-order stationary points of heterogeneous federated learning (FL). Previous works in FL mostly focus on first-order convergence guarantees, which do not rule out the scenario of unstable saddle points. Meanwhile, it is a key bottleneck of FL to achieve communication efficiency without compensating the learning accuracy, especially when local data are highly heterogeneous across different clients. Given this, we propose a novel algorithm Power-EF that only communicates compressed information via a novel error-feedback scheme. To our knowledge, Power-EF is the first distributed and compressed SGD algorithm that provably escapes saddle points in heterogeneous FL without any data homogeneity assumptions. In particular, Power-EF improves to second-order stationary points after visiting first-order (possibly saddle) points, using additional gradient queries and communication rounds only of almost the same order required by first-order convergence, and the convergence rate exhibits a linear speedup in terms of the number of workers. Our theory improves/recovers previous results, while extending to much more tolerant settings on the local data. Numerical experiments are provided to complement the theory.

Coresets for Vertical Federated Learning: Regularized Linear Regression and $K$-Means Clustering

Vertical federated learning (VFL), where data features are stored in multiple parties distributively, is an important area in machine learning. However, the communication complexity for VFL is typically very high. In this paper, we propose a unified framework by constructing coresets in a distributed fashion for communication-efficient VFL. We study two important learning tasks in the VFL setting: regularized linear regression and $k$-means clustering, and apply our coreset framework to both problems. We theoretically show that using coresets can drastically alleviate the communication complexity, while nearly maintain the solution quality. Numerical experiments are conducted to corroborate our theoretical findings.

Simple and Optimal Stochastic Gradient Methods for Nonsmooth Nonconvex Optimization

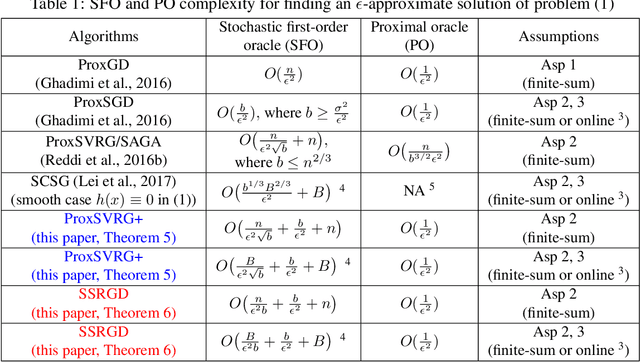
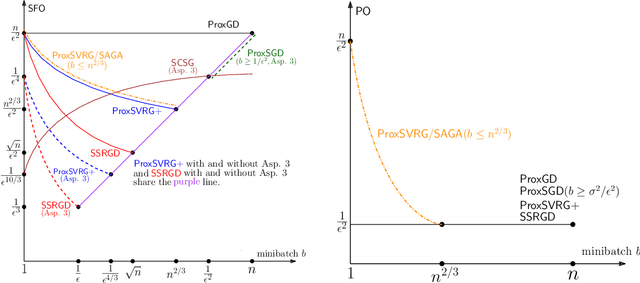
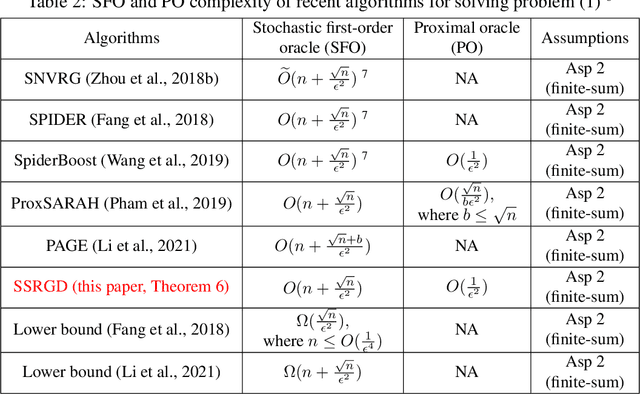
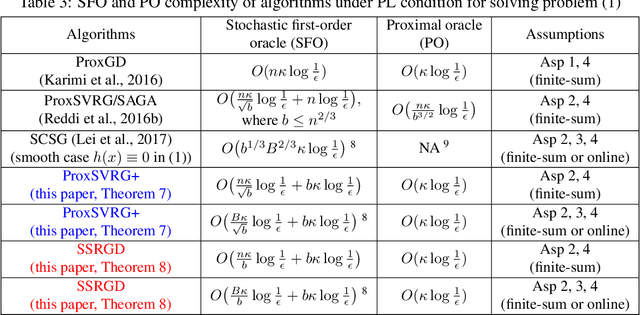
We propose and analyze several stochastic gradient algorithms for finding stationary points or local minimum in nonconvex, possibly with nonsmooth regularizer, finite-sum and online optimization problems. First, we propose a simple proximal stochastic gradient algorithm based on variance reduction called ProxSVRG+. We provide a clean and tight analysis of ProxSVRG+, which shows that it outperforms the deterministic proximal gradient descent (ProxGD) for a wide range of minibatch sizes, hence solves an open problem proposed in Reddi et al. (2016b). Also, ProxSVRG+ uses much less proximal oracle calls than ProxSVRG (Reddi et al., 2016b) and extends to the online setting by avoiding full gradient computations. Then, we further propose an optimal algorithm, called SSRGD, based on SARAH (Nguyen et al., 2017) and show that SSRGD further improves the gradient complexity of ProxSVRG+ and achieves the optimal upper bound, matching the known lower bound of (Fang et al., 2018; Li et al., 2021). Moreover, we show that both ProxSVRG+ and SSRGD enjoy automatic adaptation with local structure of the objective function such as the Polyak-\L{}ojasiewicz (PL) condition for nonconvex functions in the finite-sum case, i.e., we prove that both of them can automatically switch to faster global linear convergence without any restart performed in prior work ProxSVRG (Reddi et al., 2016b). Finally, we focus on the more challenging problem of finding an $(\epsilon, \delta)$-local minimum instead of just finding an $\epsilon$-approximate (first-order) stationary point (which may be some bad unstable saddle points). We show that SSRGD can find an $(\epsilon, \delta)$-local minimum by simply adding some random perturbations. Our algorithm is almost as simple as its counterpart for finding stationary points, and achieves similar optimal rates.

SoteriaFL: A Unified Framework for Private Federated Learning with Communication Compression

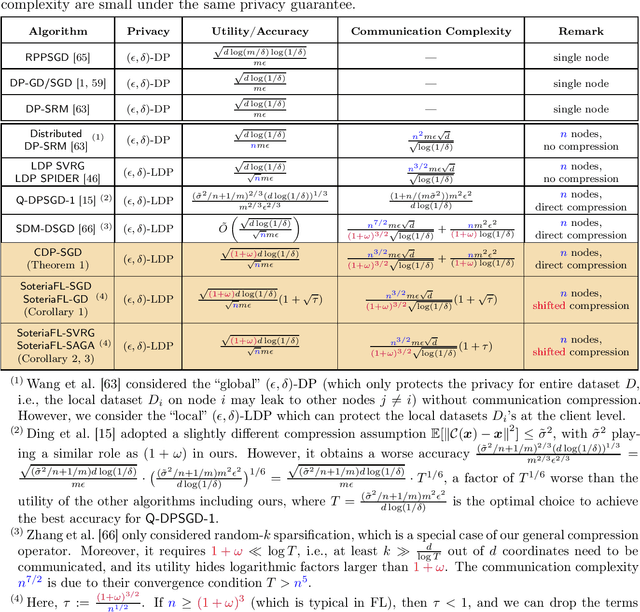
To enable large-scale machine learning in bandwidth-hungry environments such as wireless networks, significant progress has been made recently in designing communication-efficient federated learning algorithms with the aid of communication compression. On the other end, privacy-preserving, especially at the client level, is another important desideratum that has not been addressed simultaneously in the presence of advanced communication compression techniques yet. In this paper, we propose a unified framework that enhances the communication efficiency of private federated learning with communication compression. Exploiting both general compression operators and local differential privacy, we first examine a simple algorithm that applies compression directly to differentially-private stochastic gradient descent, and identify its limitations. We then propose a unified framework SoteriaFL for private federated learning, which accommodates a general family of local gradient estimators including popular stochastic variance-reduced gradient methods and the state-of-the-art shifted compression scheme. We provide a comprehensive characterization of its performance trade-offs in terms of privacy, utility, and communication complexity, where SoteraFL is shown to achieve better communication complexity without sacrificing privacy nor utility than other private federated learning algorithms without communication compression.

3PC: Three Point Compressors for Communication-Efficient Distributed Training and a Better Theory for Lazy Aggregation

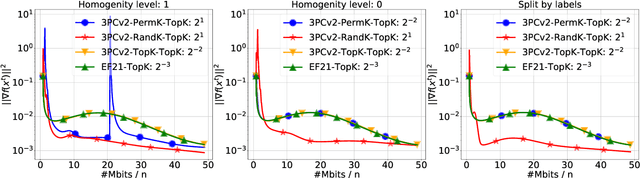
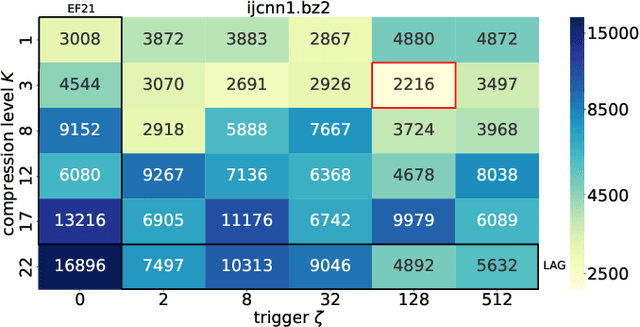
We propose and study a new class of gradient communication mechanisms for communication-efficient training -- three point compressors (3PC) -- as well as efficient distributed nonconvex optimization algorithms that can take advantage of them. Unlike most established approaches, which rely on a static compressor choice (e.g., Top-$K$), our class allows the compressors to {\em evolve} throughout the training process, with the aim of improving the theoretical communication complexity and practical efficiency of the underlying methods. We show that our general approach can recover the recently proposed state-of-the-art error feedback mechanism EF21 (Richt\'arik et al., 2021) and its theoretical properties as a special case, but also leads to a number of new efficient methods. Notably, our approach allows us to improve upon the state of the art in the algorithmic and theoretical foundations of the {\em lazy aggregation} literature (Chen et al., 2018). As a by-product that may be of independent interest, we provide a new and fundamental link between the lazy aggregation and error feedback literature. A special feature of our work is that we do not require the compressors to be unbiased.

BEER: Fast $O$ Rate for Decentralized Nonconvex Optimization with Communication Compression

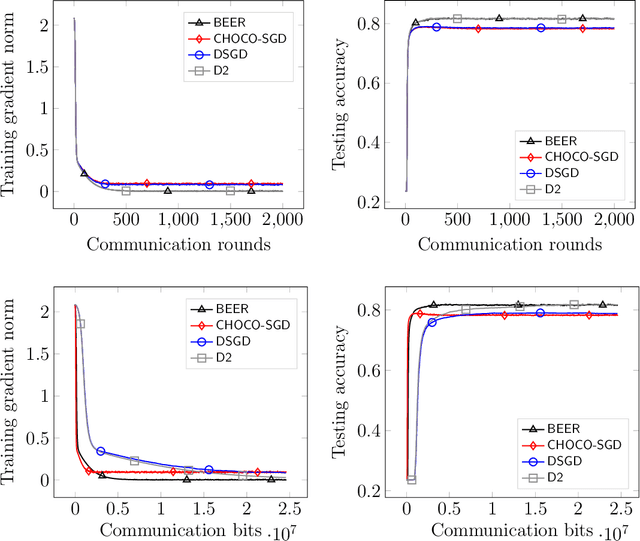
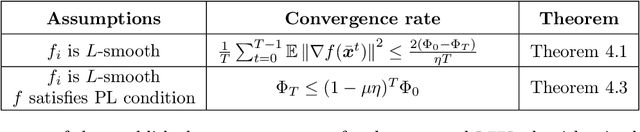
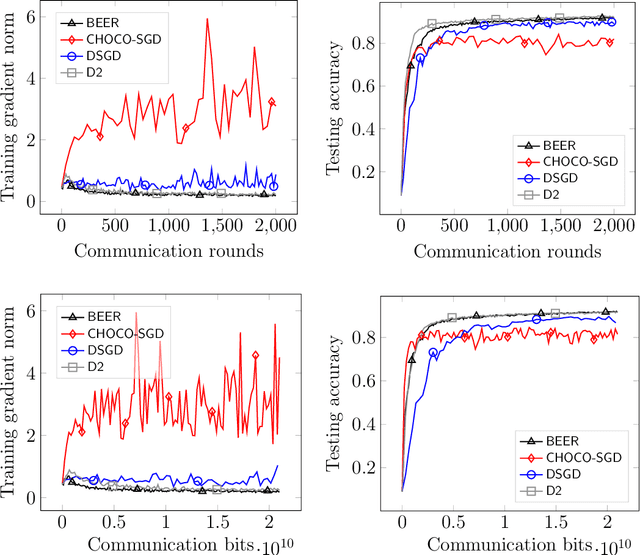
Communication efficiency has been widely recognized as the bottleneck for large-scale decentralized machine learning applications in multi-agent or federated environments. To tackle the communication bottleneck, there have been many efforts to design communication-compressed algorithms for decentralized nonconvex optimization, where the clients are only allowed to communicate a small amount of quantized information (aka bits) with their neighbors over a predefined graph topology. Despite significant efforts, the state-of-the-art algorithm in the nonconvex setting still suffers from a slower rate of convergence $O((G/T)^{2/3})$ compared with their uncompressed counterpart, where $G$ measures the data heterogeneity across different clients, and $T$ is the number of communication rounds. This paper proposes BEER, which adopts communication compression with gradient tracking, and shows it converges at a faster rate of $O(1/T)$. This significantly improves over the state-of-the-art rate, by matching the rate without compression even under arbitrary data heterogeneity. Numerical experiments are also provided to corroborate our theory and confirm the practical superiority of BEER in the data heterogeneous regime.

Faster Rates for Compressed Federated Learning with Client-Variance Reduction

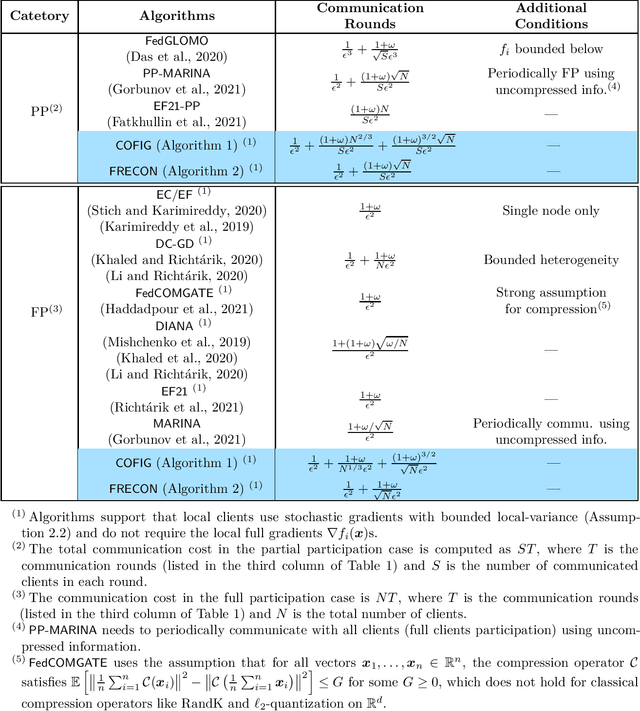
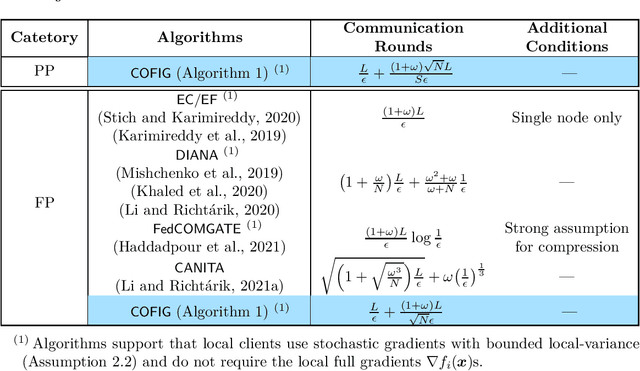
Due to the communication bottleneck in distributed and federated learning applications, algorithms using communication compression have attracted significant attention and are widely used in practice. Moreover, there exists client-variance in federated learning due to the total number of heterogeneous clients is usually very large and the server is unable to communicate with all clients in each communication round. In this paper, we address these two issues together by proposing compressed and client-variance reduced methods. Concretely, we introduce COFIG and FRECON, which successfully enjoy communication compression with client-variance reduction. The total communication round of COFIG is $O(\frac{(1+\omega)^{3/2}\sqrt{N}}{S\epsilon^2}+\frac{(1+\omega)N^{2/3}}{S\epsilon^2})$ in the nonconvex setting, where $N$ is the total number of clients, $S$ is the number of communicated clients in each round, $\epsilon$ is the convergence error, and $\omega$ is the parameter for the compression operator. Besides, our FRECON can converge faster than COFIG in the nonconvex setting, and it converges with $O(\frac{(1+\omega)\sqrt{N}}{S\epsilon^2})$ communication rounds. In the convex setting, COFIG converges within the communication rounds $O(\frac{(1+\omega)\sqrt{N}}{S\epsilon})$, which is also the first convergence result for compression schemes that do not communicate with all the clients in each round. In sum, both COFIG and FRECON do not need to communicate with all the clients and provide first/faster convergence results for convex and nonconvex federated learning, while previous works either require full clients communication (thus not practical) or obtain worse convergence results.

EF21 with Bells & Whistles: Practical Algorithmic Extensions of Modern Error Feedback

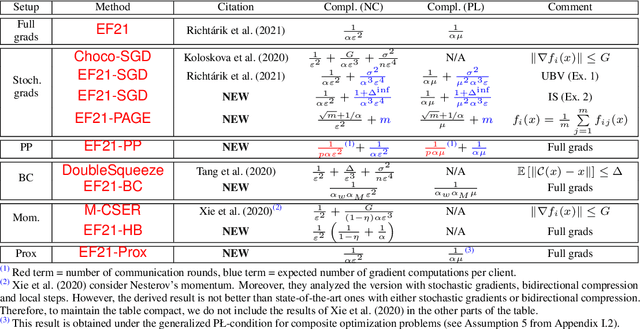
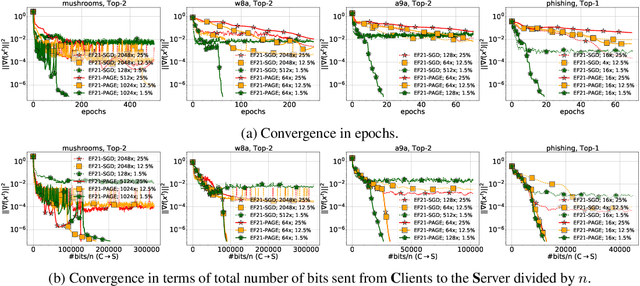
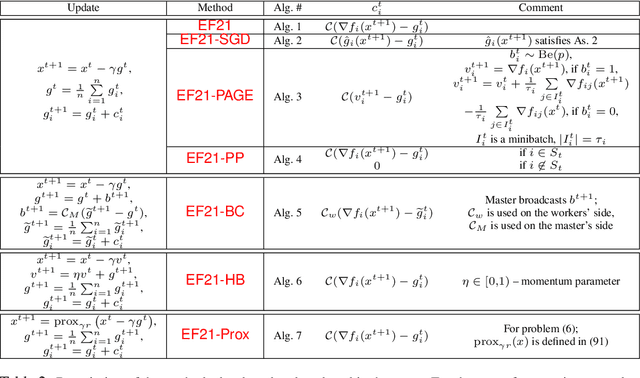
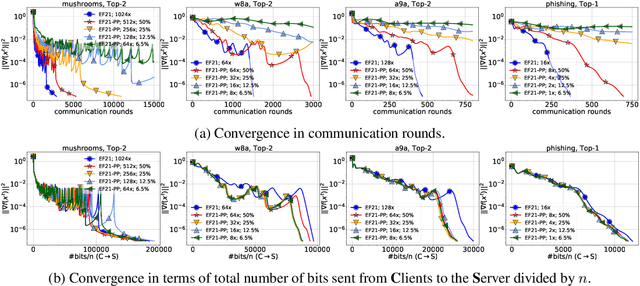
First proposed by Seide (2014) as a heuristic, error feedback (EF) is a very popular mechanism for enforcing convergence of distributed gradient-based optimization methods enhanced with communication compression strategies based on the application of contractive compression operators. However, existing theory of EF relies on very strong assumptions (e.g., bounded gradients), and provides pessimistic convergence rates (e.g., while the best known rate for EF in the smooth nonconvex regime, and when full gradients are compressed, is $O(1/T^{2/3})$, the rate of gradient descent in the same regime is $O(1/T)$). Recently, Richt\'{a}rik et al. (2021) proposed a new error feedback mechanism, EF21, based on the construction of a Markov compressor induced by a contractive compressor. EF21 removes the aforementioned theoretical deficiencies of EF and at the same time works better in practice. In this work we propose six practical extensions of EF21, all supported by strong convergence theory: partial participation, stochastic approximation, variance reduction, proximal setting, momentum and bidirectional compression. Several of these techniques were never analyzed in conjunction with EF before, and in cases where they were (e.g., bidirectional compression), our rates are vastly superior.

DESTRESS: Computation-Optimal and Communication-Efficient Decentralized Nonconvex Finite-Sum Optimization

Emerging applications in multi-agent environments such as internet-of-things, networked sensing, autonomous systems and federated learning, call for decentralized algorithms for finite-sum optimizations that are resource-efficient in terms of both computation and communication. In this paper, we consider the prototypical setting where the agents work collaboratively to minimize the sum of local loss functions by only communicating with their neighbors over a predetermined network topology. We develop a new algorithm, called DEcentralized STochastic REcurSive gradient methodS (DESTRESS) for nonconvex finite-sum optimization, which matches the optimal incremental first-order oracle (IFO) complexity of centralized algorithms for finding first-order stationary points, while maintaining communication efficiency. Detailed theoretical and numerical comparisons corroborate that the resource efficiencies of DESTRESS improve upon prior decentralized algorithms over a wide range of parameter regimes. DESTRESS leverages several key algorithm design ideas including stochastic recursive gradient updates with mini-batches for local computation, gradient tracking with extra mixing (i.e., multiple gossiping rounds) for per-iteration communication, together with careful choices of hyper-parameters and new analysis frameworks to provably achieve a desirable computation-communication trade-off.