STAR: Semantic-Traffic Alignment and Retrieval for Zero-Shot HTTPS Website Fingerprinting

Modern HTTPS mechanisms such as Encrypted Client Hello (ECH) and encrypted DNS improve privacy but remain vulnerable to website fingerprinting (WF) attacks, where adversaries infer visited sites from encrypted traffic patterns. Existing WF methods rely on supervised learning with site-specific labeled traces, which limits scalability and fails to handle previously unseen websites. We address these limitations by reformulating WF as a zero-shot cross-modal retrieval problem and introducing STAR. STAR learns a joint embedding space for encrypted traffic traces and crawl-time logic profiles using a dual-encoder architecture. Trained on 150K automatically collected traffic-logic pairs with contrastive and consistency objectives and structure-aware augmentation, STAR retrieves the most semantically aligned profile for a trace without requiring target-side traffic during training. Experiments on 1,600 unseen websites show that STAR achieves 87.9 percent top-1 accuracy and 0.963 AUC in open-world detection, outperforming supervised and few-shot baselines. Adding an adapter with only four labeled traces per site further boosts top-5 accuracy to 98.8 percent. Our analysis reveals intrinsic semantic-traffic alignment in modern web protocols, identifying semantic leakage as the dominant privacy risk in encrypted HTTPS traffic. We release STAR's datasets and code to support reproducibility and future research.

LightSAM: Parameter-Agnostic Sharpness-Aware Minimization

Sharpness-Aware Minimization (SAM) optimizer enhances the generalization ability of the machine learning model by exploring the flat minima landscape through weight perturbations. Despite its empirical success, SAM introduces an additional hyper-parameter, the perturbation radius, which causes the sensitivity of SAM to it. Moreover, it has been proved that the perturbation radius and learning rate of SAM are constrained by problem-dependent parameters to guarantee convergence. These limitations indicate the requirement of parameter-tuning in practical applications. In this paper, we propose the algorithm LightSAM which sets the perturbation radius and learning rate of SAM adaptively, thus extending the application scope of SAM. LightSAM employs three popular adaptive optimizers, including AdaGrad-Norm, AdaGrad and Adam, to replace the SGD optimizer for weight perturbation and model updating, reducing sensitivity to parameters. Theoretical results show that under weak assumptions, LightSAM could converge ideally with any choices of perturbation radius and learning rate, thus achieving parameter-agnostic. We conduct preliminary experiments on several deep learning tasks, which together with the theoretical findings validate the the effectiveness of LightSAM.

Communication-Efficient Distributed Learning with Local Immediate Error Compensation

Gradient compression with error compensation has attracted significant attention with the target of reducing the heavy communication overhead in distributed learning. However, existing compression methods either perform only unidirectional compression in one iteration with higher communication cost, or bidirectional compression with slower convergence rate. In this work, we propose the Local Immediate Error Compensated SGD (LIEC-SGD) optimization algorithm to break the above bottlenecks based on bidirectional compression and carefully designed compensation approaches. Specifically, the bidirectional compression technique is to reduce the communication cost, and the compensation technique compensates the local compression error to the model update immediately while only maintaining the global error variable on the server throughout the iterations to boost its efficacy. Theoretically, we prove that LIEC-SGD is superior to previous works in either the convergence rate or the communication cost, which indicates that LIEC-SGD could inherit the dual advantages from unidirectional compression and bidirectional compression. Finally, experiments of training deep neural networks validate the effectiveness of the proposed LIEC-SGD algorithm.

DropIT: Dropping Intermediate Tensors for Memory-Efficient DNN Training

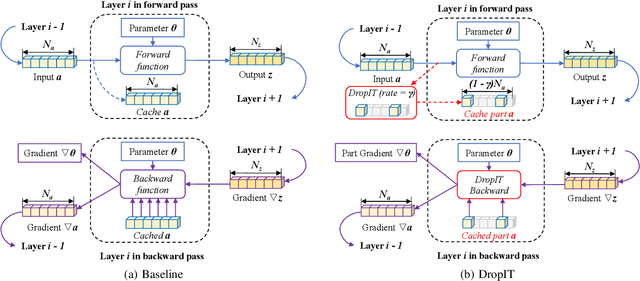
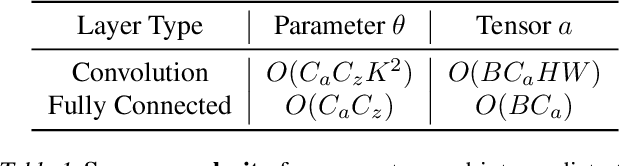
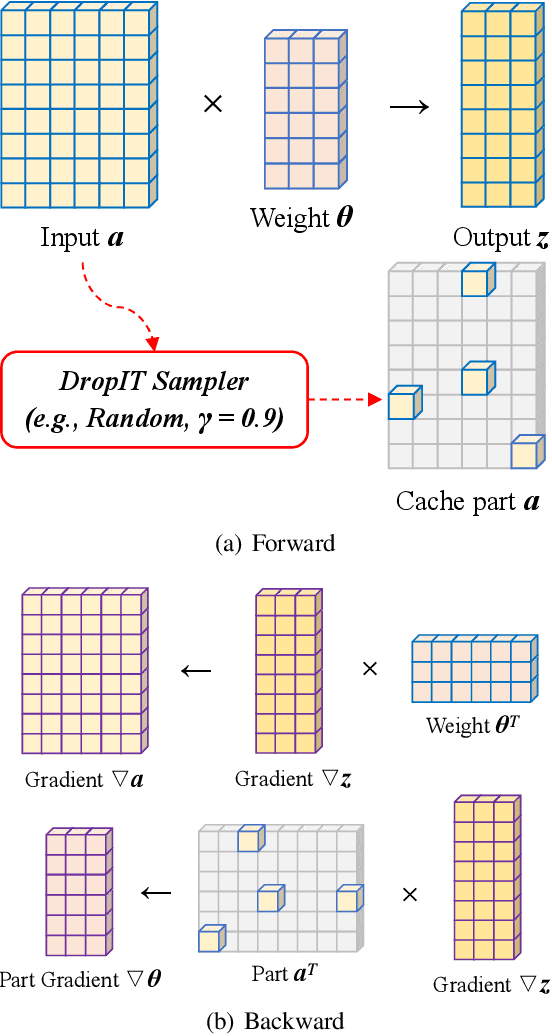
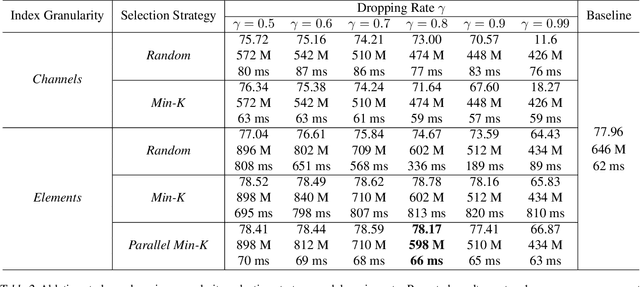
A standard hardware bottleneck when training deep neural networks is GPU memory. The bulk of memory is occupied by caching intermediate tensors for gradient computation in the backward pass. We propose a novel method to reduce this footprint by selecting and caching part of intermediate tensors for gradient computation. Our Intermediate Tensor Drop method (DropIT) adaptively drops components of the intermediate tensors and recovers sparsified tensors from the remaining elements in the backward pass to compute the gradient. Experiments show that we can drop up to 90% of the elements of the intermediate tensors in convolutional and fully-connected layers, saving 20% GPU memory during training while achieving higher test accuracy for standard backbones such as ResNet and Vision Transformer. Our code is available at https://github.com/ChenJoya/dropit.

STL-SGD: Speeding Up Local SGD with Stagewise Communication Period

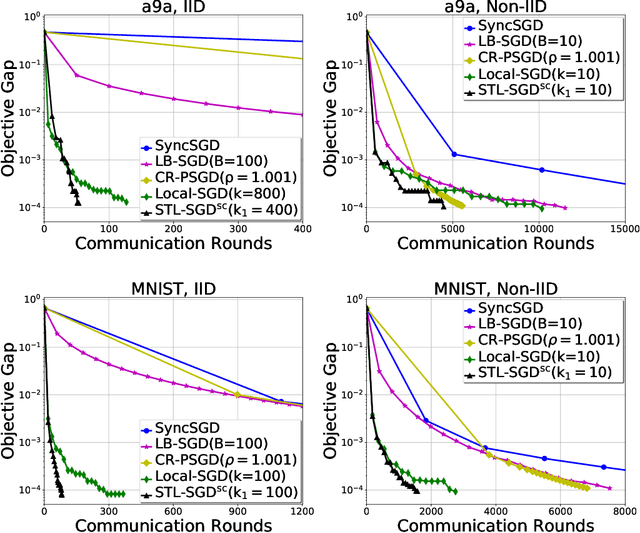
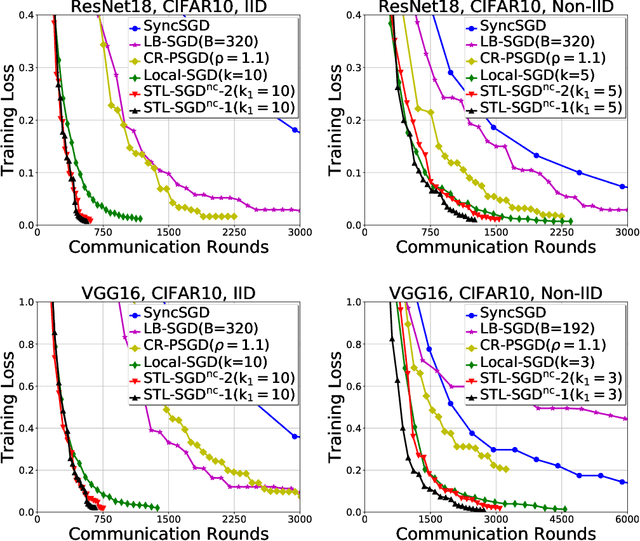
Distributed parallel stochastic gradient descent algorithms are workhorses for large scale machine learning tasks. Among them, local stochastic gradient descent (Local SGD) has attracted significant attention due to its low communication complexity. Previous studies prove that the communication complexity of Local SGD with a fixed or an adaptive communication period is in the order of $O (N^{\frac{3}{2}} T^{\frac{1}{2}})$ and $O (N^{\frac{3}{4}} T^{\frac{3}{4}})$ when the data distributions on clients are identical (IID) or otherwise (Non-IID). In this paper, to accelerate the convergence by reducing the communication complexity, we propose \textit{ST}agewise \textit{L}ocal \textit{SGD} (STL-SGD), which increases the communication period gradually along with decreasing learning rate. We prove that STL-SGD can keep the same convergence rate and linear speedup as mini-batch SGD. In addition, as the benefit of increasing the communication period, when the objective is strongly convex or satisfies the Polyak-\L ojasiewicz condition, the communication complexity of STL-SGD is $O (N \log{T})$ and $O (N^{\frac{1}{2}} T^{\frac{1}{2}})$ for the IID case and the Non-IID case respectively, achieving significant improvements over Local SGD. Experiments on both convex and non-convex problems demonstrate the superior performance of STL-SGD.

Variance Reduced Local SGD with Lower Communication Complexity

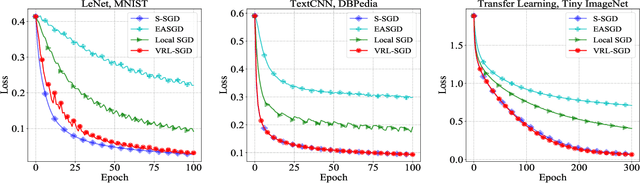
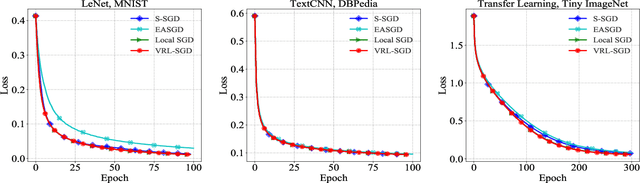
To accelerate the training of machine learning models, distributed stochastic gradient descent (SGD) and its variants have been widely adopted, which apply multiple workers in parallel to speed up training. Among them, Local SGD has gained much attention due to its lower communication cost. Nevertheless, when the data distribution on workers is non-identical, Local SGD requires $O(T^{\frac{3}{4}} N^{\frac{3}{4}})$ communications to maintain its \emph{linear iteration speedup} property, where $T$ is the total number of iterations and $N$ is the number of workers. In this paper, we propose Variance Reduced Local SGD (VRL-SGD) to further reduce the communication complexity. Benefiting from eliminating the dependency on the gradient variance among workers, we theoretically prove that VRL-SGD achieves a \emph{linear iteration speedup} with a lower communication complexity $O(T^{\frac{1}{2}} N^{\frac{3}{2}})$ even if workers access non-identical datasets. We conduct experiments on three machine learning tasks, and the experimental results demonstrate that VRL-SGD performs impressively better than Local SGD when the data among workers are quite diverse.

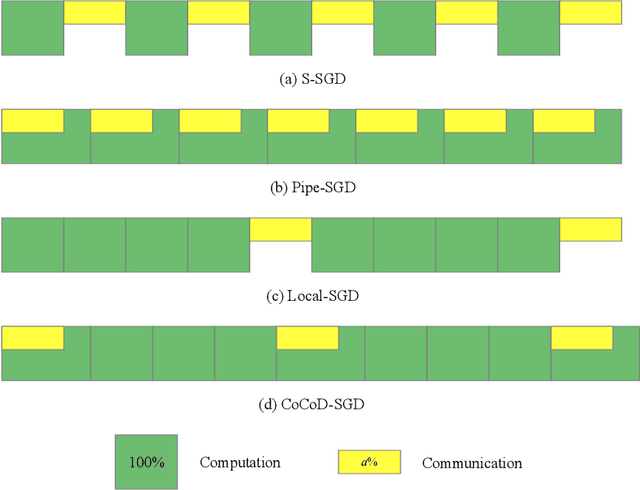
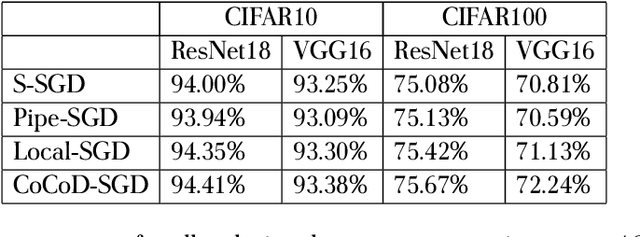
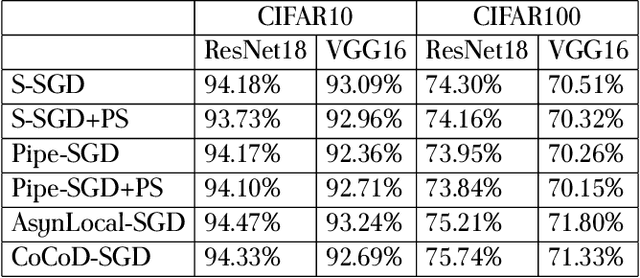
Faster Distributed Deep Net Training: Computation and Communication Decoupled Stochastic Gradient Descent

With the increase in the amount of data and the expansion of model scale, distributed parallel training becomes an important and successful technique to address the optimization challenges. Nevertheless, although distributed stochastic gradient descent (SGD) algorithms can achieve a linear iteration speedup, they are limited significantly in practice by the communication cost, making it difficult to achieve a linear time speedup. In this paper, we propose a computation and communication decoupled stochastic gradient descent (CoCoD-SGD) algorithm to run computation and communication in parallel to reduce the communication cost. We prove that CoCoD-SGD has a linear iteration speedup with respect to the total computation capability of the hardware resources. In addition, it has a lower communication complexity and better time speedup comparing with traditional distributed SGD algorithms. Experiments on deep neural network training demonstrate the significant improvements of CoCoD-SGD: when training ResNet18 and VGG16 with 16 Geforce GTX 1080Ti GPUs, CoCoD-SGD is up to 2-3$\times$ faster than traditional synchronous SGD.