Meta Lattice: Model Space Redesign for Cost-Effective Industry-Scale Ads Recommendations

The rapidly evolving landscape of products, surfaces, policies, and regulations poses significant challenges for deploying state-of-the-art recommendation models at industry scale, primarily due to data fragmentation across domains and escalating infrastructure costs that hinder sustained quality improvements. To address this challenge, we propose Lattice, a recommendation framework centered around model space redesign that extends Multi-Domain, Multi-Objective (MDMO) learning beyond models and learning objectives. Lattice addresses these challenges through a comprehensive model space redesign that combines cross-domain knowledge sharing, data consolidation, model unification, distillation, and system optimizations to achieve significant improvements in both quality and cost-efficiency. Our deployment of Lattice at Meta has resulted in 10% revenue-driving top-line metrics gain, 11.5% user satisfaction improvement, 6% boost in conversion rate, with 20% capacity saving.

Enhancing Embedding Representation Stability in Recommendation Systems with Semantic ID

The exponential growth of online content has posed significant challenges to ID-based models in industrial recommendation systems, ranging from extremely high cardinality and dynamically growing ID space, to highly skewed engagement distributions, to prediction instability as a result of natural id life cycles (e.g, the birth of new IDs and retirement of old IDs). To address these issues, many systems rely on random hashing to handle the id space and control the corresponding model parameters (i.e embedding table). However, this approach introduces data pollution from multiple ids sharing the same embedding, leading to degraded model performance and embedding representation instability. This paper examines these challenges and introduces Semantic ID prefix ngram, a novel token parameterization technique that significantly improves the performance of the original Semantic ID. Semantic ID prefix ngram creates semantically meaningful collisions by hierarchically clustering items based on their content embeddings, as opposed to random assignments. Through extensive experimentation, we demonstrate that Semantic ID prefix ngram not only addresses embedding instability but also significantly improves tail id modeling, reduces overfitting, and mitigates representation shifts. We further highlight the advantages of Semantic ID prefix ngram in attention-based models that contextualize user histories, showing substantial performance improvements. We also report our experience of integrating Semantic ID into Meta production Ads Ranking system, leading to notable performance gains and enhanced prediction stability in live deployments.

External Large Foundation Model: How to Efficiently Serve Trillions of Parameters for Online Ads Recommendation

Ads recommendation is a prominent service of online advertising systems and has been actively studied. Recent studies indicate that scaling-up and advanced design of the recommendation model can bring significant performance improvement. However, with a larger model scale, such prior studies have a significantly increasing gap from industry as they often neglect two fundamental challenges in industrial-scale applications. First, training and inference budgets are restricted for the model to be served, exceeding which may incur latency and impair user experience. Second, large-volume data arrive in a streaming mode with data distributions dynamically shifting, as new users/ads join and existing users/ads leave the system. We propose the External Large Foundation Model (ExFM) framework to address the overlooked challenges. Specifically, we develop external distillation and a data augmentation system (DAS) to control the computational cost of training/inference while maintaining high performance. We design the teacher in a way like a foundation model (FM) that can serve multiple students as vertical models (VMs) to amortize its building cost. We propose Auxiliary Head and Student Adapter to mitigate the data distribution gap between FM and VMs caused by the streaming data issue. Comprehensive experiments on internal industrial-scale applications and public datasets demonstrate significant performance gain by ExFM.

Fine-Grained Embedding Dimension Optimization During Training for Recommender Systems

Huge embedding tables in modern Deep Learning Recommender Models (DLRM) require prohibitively large memory during training and inference. Aiming to reduce the memory footprint of training, this paper proposes FIne-grained In-Training Embedding Dimension optimization (FIITED). Given the observation that embedding vectors are not equally important, FIITED adjusts the dimension of each individual embedding vector continuously during training, assigning longer dimensions to more important embeddings while adapting to dynamic changes in data. A novel embedding storage system based on virtually-hashed physically-indexed hash tables is designed to efficiently implement the embedding dimension adjustment and effectively enable memory saving. Experiments on two industry models show that FIITED is able to reduce the size of embeddings by more than 65% while maintaining the trained model's quality, saving significantly more memory than a state-of-the-art in-training embedding pruning method. On public click-through rate prediction datasets, FIITED is able to prune up to 93.75%-99.75% embeddings without significant accuracy loss.

Provably Efficient Generalized Lagrangian Policy Optimization for Safe Multi-Agent Reinforcement Learning

We examine online safe multi-agent reinforcement learning using constrained Markov games in which agents compete by maximizing their expected total rewards under a constraint on expected total utilities. Our focus is confined to an episodic two-player zero-sum constrained Markov game with independent transition functions that are unknown to agents, adversarial reward functions, and stochastic utility functions. For such a Markov game, we employ an approach based on the occupancy measure to formulate it as an online constrained saddle-point problem with an explicit constraint. We extend the Lagrange multiplier method in constrained optimization to handle the constraint by creating a generalized Lagrangian with minimax decision primal variables and a dual variable. Next, we develop an upper confidence reinforcement learning algorithm to solve this Lagrangian problem while balancing exploration and exploitation. Our algorithm updates the minimax decision primal variables via online mirror descent and the dual variable via projected gradient step and we prove that it enjoys sublinear rate $ O((|X|+|Y|) L \sqrt{T(|A|+|B|)}))$ for both regret and constraint violation after playing $T$ episodes of the game. Here, $L$ is the horizon of each episode, $(|X|,|A|)$ and $(|Y|,|B|)$ are the state/action space sizes of the min-player and the max-player, respectively. To the best of our knowledge, we provide the first provably efficient online safe reinforcement learning algorithm in constrained Markov games.

Provably Efficient Fictitious Play Policy Optimization for Zero-Sum Markov Games with Structured Transitions

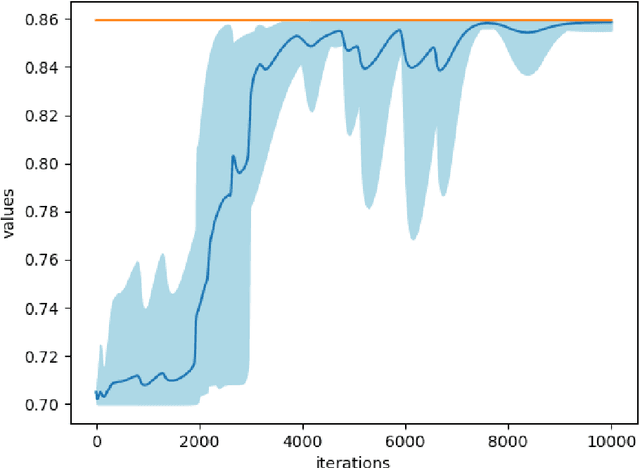
While single-agent policy optimization in a fixed environment has attracted a lot of research attention recently in the reinforcement learning community, much less is known theoretically when there are multiple agents playing in a potentially competitive environment. We take steps forward by proposing and analyzing new fictitious play policy optimization algorithms for zero-sum Markov games with structured but unknown transitions. We consider two classes of transition structures: factored independent transition and single-controller transition. For both scenarios, we prove tight $\widetilde{\mathcal{O}}(\sqrt{K})$ regret bounds after $K$ episodes in a two-agent competitive game scenario. The regret of each agent is measured against a potentially adversarial opponent who can choose a single best policy in hindsight after observing the full policy sequence. Our algorithms feature a combination of Upper Confidence Bound (UCB)-type optimism and fictitious play under the scope of simultaneous policy optimization in a non-stationary environment. When both players adopt the proposed algorithms, their overall optimality gap is $\widetilde{\mathcal{O}}(\sqrt{K})$.

DHEN: A Deep and Hierarchical Ensemble Network for Large-Scale Click-Through Rate Prediction

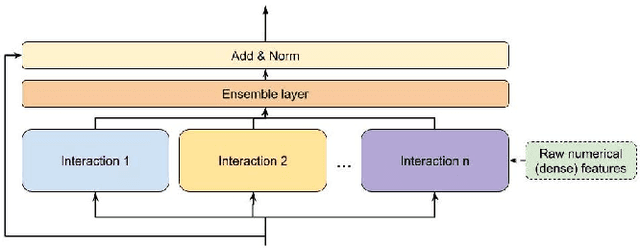
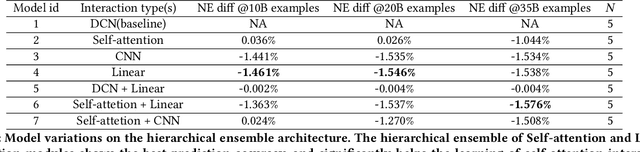
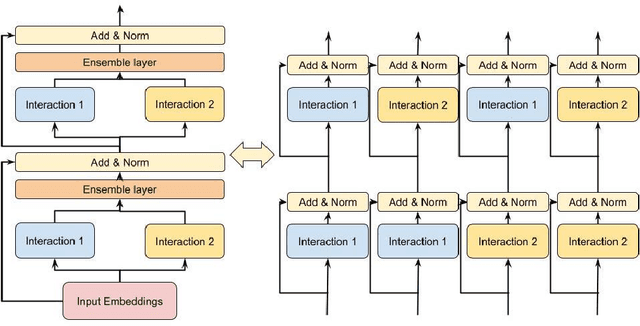
Learning feature interactions is important to the model performance of online advertising services. As a result, extensive efforts have been devoted to designing effective architectures to learn feature interactions. However, we observe that the practical performance of those designs can vary from dataset to dataset, even when the order of interactions claimed to be captured is the same. That indicates different designs may have different advantages and the interactions captured by them have non-overlapping information. Motivated by this observation, we propose DHEN - a deep and hierarchical ensemble architecture that can leverage strengths of heterogeneous interaction modules and learn a hierarchy of the interactions under different orders. To overcome the challenge brought by DHEN's deeper and multi-layer structure in training, we propose a novel co-designed training system that can further improve the training efficiency of DHEN. Experiments of DHEN on large-scale dataset from CTR prediction tasks attained 0.27\% improvement on the Normalized Entropy (NE) of prediction and 1.2x better training throughput than state-of-the-art baseline, demonstrating their effectiveness in practice.

Frequency-aware SGD for Efficient Embedding Learning with Provable Benefits

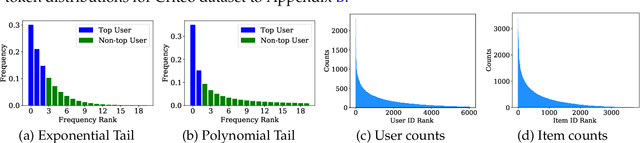
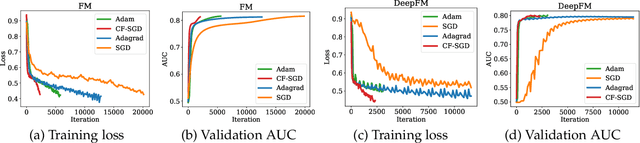
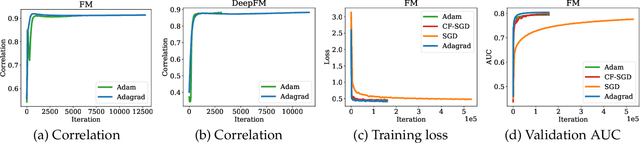
Embedding learning has found widespread applications in recommendation systems and natural language modeling, among other domains. To learn quality embeddings efficiently, adaptive learning rate algorithms have demonstrated superior empirical performance over SGD, largely accredited to their token-dependent learning rate. However, the underlying mechanism for the efficiency of token-dependent learning rate remains underexplored. We show that incorporating frequency information of tokens in the embedding learning problems leads to provably efficient algorithms, and demonstrate that common adaptive algorithms implicitly exploit the frequency information to a large extent. Specifically, we propose (Counter-based) Frequency-aware Stochastic Gradient Descent, which applies a frequency-dependent learning rate for each token, and exhibits provable speed-up compared to SGD when the token distribution is imbalanced. Empirically, we show the proposed algorithms are able to improve or match adaptive algorithms on benchmark recommendation tasks and a large-scale industrial recommendation system, closing the performance gap between SGD and adaptive algorithms. Our results are the first to show token-dependent learning rate provably improves convergence for non-convex embedding learning problems.

Low-Precision Hardware Architectures Meet Recommendation Model Inference at Scale

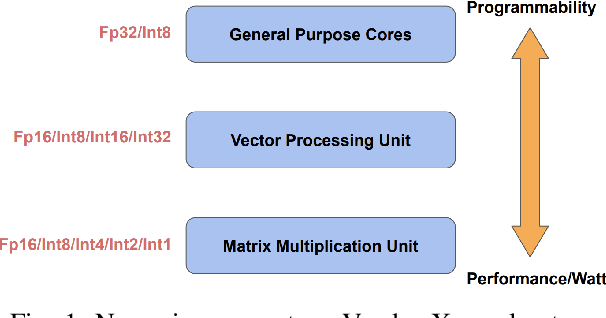
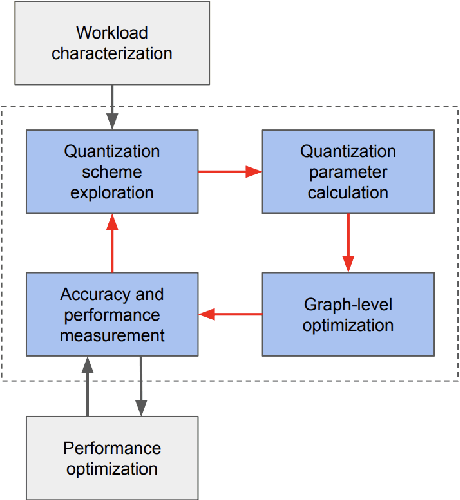
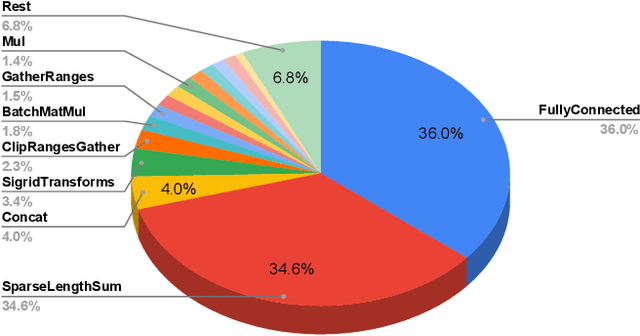
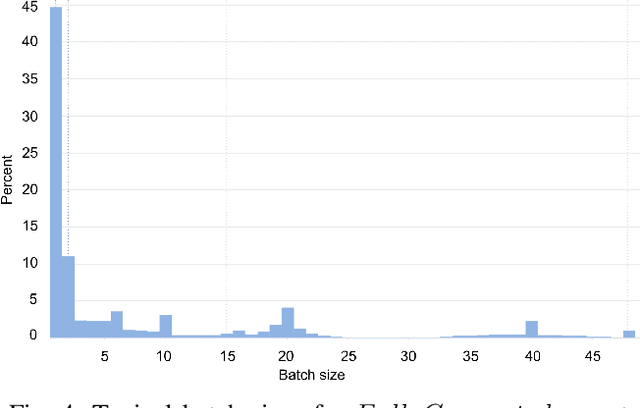
Tremendous success of machine learning (ML) and the unabated growth in ML model complexity motivated many ML-specific designs in both CPU and accelerator architectures to speed up the model inference. While these architectures are diverse, highly optimized low-precision arithmetic is a component shared by most. Impressive compute throughputs are indeed often exhibited by these architectures on benchmark ML models. Nevertheless, production models such as recommendation systems important to Facebook's personalization services are demanding and complex: These systems must serve billions of users per month responsively with low latency while maintaining high prediction accuracy, notwithstanding computations with many tens of billions parameters per inference. Do these low-precision architectures work well with our production recommendation systems? They do. But not without significant effort. We share in this paper our search strategies to adapt reference recommendation models to low-precision hardware, our optimization of low-precision compute kernels, and the design and development of tool chain so as to maintain our models' accuracy throughout their lifespan during which topic trends and users' interests inevitably evolve. Practicing these low-precision technologies helped us save datacenter capacities while deploying models with up to 5X complexity that would otherwise not be deployed on traditional general-purpose CPUs. We believe these lessons from the trenches promote better co-design between hardware architecture and software engineering and advance the state of the art of ML in industry.

Fast Distributed Training of Deep Neural Networks: Dynamic Communication Thresholding for Model and Data Parallelism

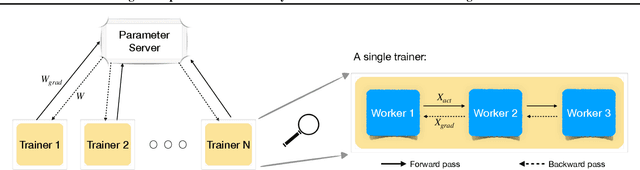
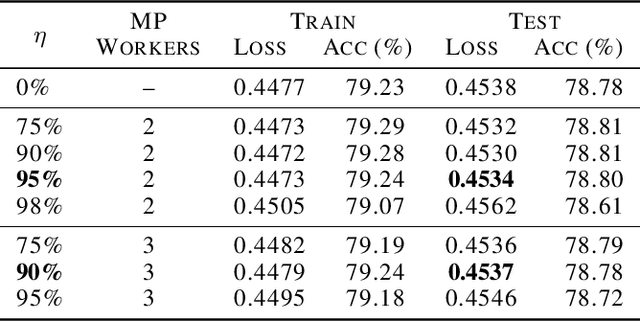
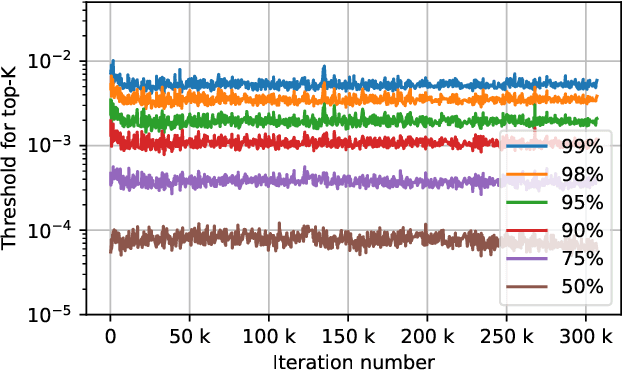
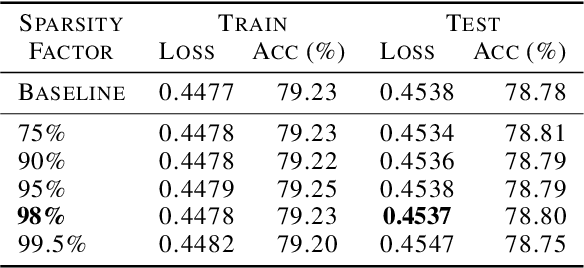
Data Parallelism (DP) and Model Parallelism (MP) are two common paradigms to enable large-scale distributed training of neural networks. Recent trends, such as the improved model performance of deeper and wider neural networks when trained with billions of data points, have prompted the use of hybrid parallelism---a paradigm that employs both DP and MP to scale further parallelization for machine learning. Hybrid training allows compute power to increase, but it runs up against the key bottleneck of communication overhead that hinders scalability. In this paper, we propose a compression framework called Dynamic Communication Thresholding (DCT) for communication-efficient hybrid training. DCT filters the entities to be communicated across the network through a simple hard-thresholding function, allowing only the most relevant information to pass through. For communication efficient DP, DCT compresses the parameter gradients sent to the parameter server during model synchronization, while compensating for the introduced errors with known techniques. For communication efficient MP, DCT incorporates a novel technique to compress the activations and gradients sent across the network during the forward and backward propagation, respectively. This is done by identifying and updating only the most relevant neurons of the neural network for each training sample in the data. Under modest assumptions, we show that the convergence of training is maintained with DCT. We evaluate DCT on natural language processing and recommender system models. DCT reduces overall communication by 20x, improving end-to-end training time on industry scale models by 37%. Moreover, we observe an improvement in the trained model performance, as the induced sparsity is possibly acting as an implicit sparsity based regularization.