Low-Precision Hardware Architectures Meet Recommendation Model Inference at Scale

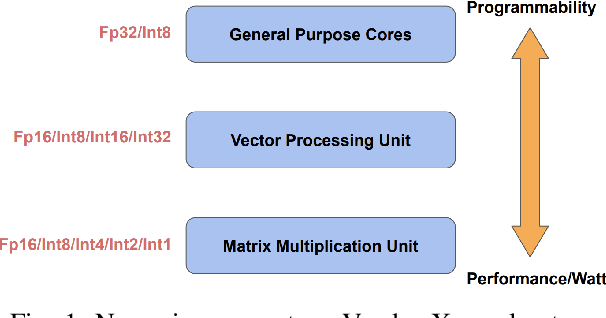
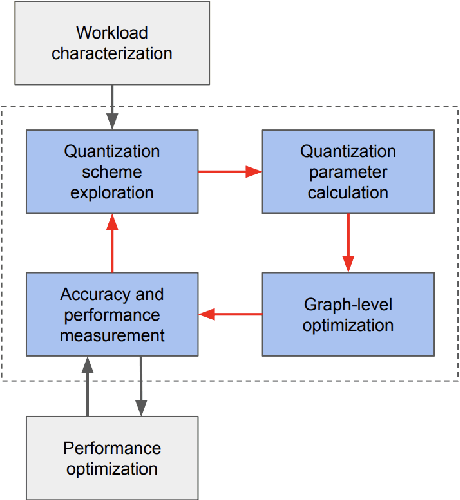
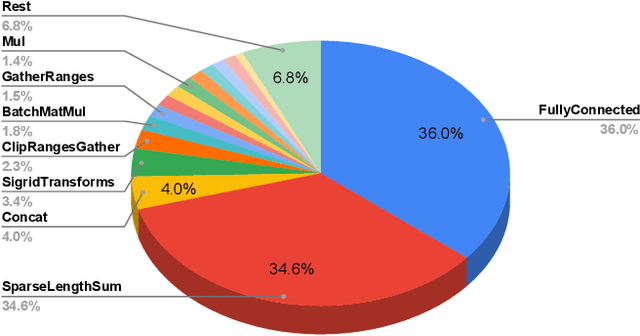
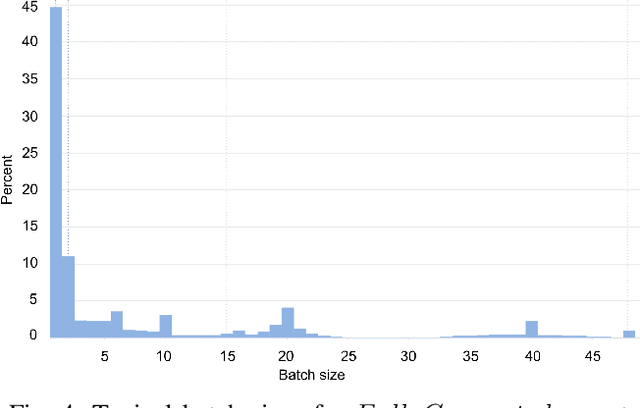
Tremendous success of machine learning (ML) and the unabated growth in ML model complexity motivated many ML-specific designs in both CPU and accelerator architectures to speed up the model inference. While these architectures are diverse, highly optimized low-precision arithmetic is a component shared by most. Impressive compute throughputs are indeed often exhibited by these architectures on benchmark ML models. Nevertheless, production models such as recommendation systems important to Facebook's personalization services are demanding and complex: These systems must serve billions of users per month responsively with low latency while maintaining high prediction accuracy, notwithstanding computations with many tens of billions parameters per inference. Do these low-precision architectures work well with our production recommendation systems? They do. But not without significant effort. We share in this paper our search strategies to adapt reference recommendation models to low-precision hardware, our optimization of low-precision compute kernels, and the design and development of tool chain so as to maintain our models' accuracy throughout their lifespan during which topic trends and users' interests inevitably evolve. Practicing these low-precision technologies helped us save datacenter capacities while deploying models with up to 5X complexity that would otherwise not be deployed on traditional general-purpose CPUs. We believe these lessons from the trenches promote better co-design between hardware architecture and software engineering and advance the state of the art of ML in industry.

Mixed-Precision Embedding Using a Cache

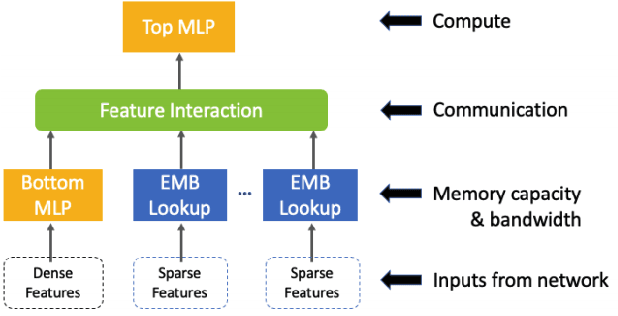
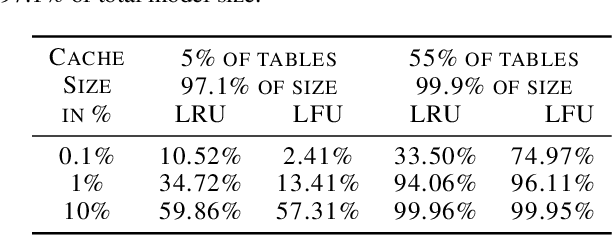
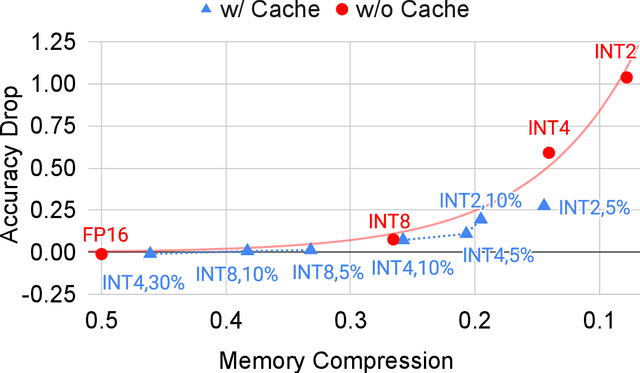
In recommendation systems, practitioners observed that increase in the number of embedding tables and their sizes often leads to significant improvement in model performances. Given this and the business importance of these models to major internet companies, embedding tables for personalization tasks have grown to terabyte scale and continue to grow at a significant rate. Meanwhile, these large-scale models are often trained with GPUs where high-performance memory is a scarce resource, thus motivating numerous work on embedding table compression during training. We propose a novel change to embedding tables using a cache memory architecture, where the majority of rows in an embedding is trained in low precision, and the most frequently or recently accessed rows cached and trained in full precision. The proposed architectural change works in conjunction with standard precision reduction and computer arithmetic techniques such as quantization and stochastic rounding. For an open source deep learning recommendation model (DLRM) running with Criteo-Kaggle dataset, we achieve 3x memory reduction with INT8 precision embedding tables and full-precision cache whose size are 5% of the embedding tables, while maintaining accuracy. For an industrial scale model and dataset, we achieve even higher >7x memory reduction with INT4 precision and cache size 1% of embedding tables, while maintaining accuracy, and 16% end-to-end training speedup by reducing GPU-to-host data transfers.

Fast Distributed Training of Deep Neural Networks: Dynamic Communication Thresholding for Model and Data Parallelism

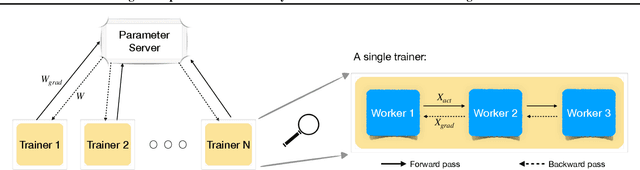
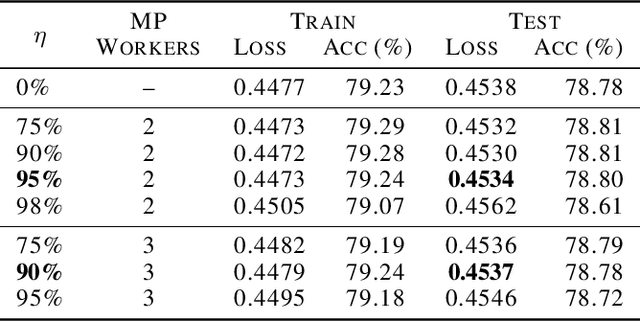
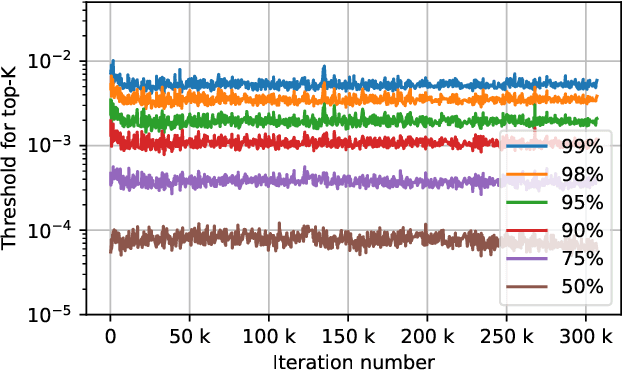
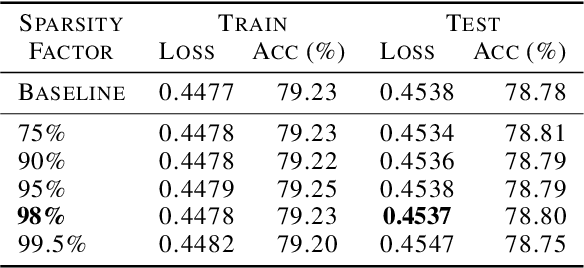
Data Parallelism (DP) and Model Parallelism (MP) are two common paradigms to enable large-scale distributed training of neural networks. Recent trends, such as the improved model performance of deeper and wider neural networks when trained with billions of data points, have prompted the use of hybrid parallelism---a paradigm that employs both DP and MP to scale further parallelization for machine learning. Hybrid training allows compute power to increase, but it runs up against the key bottleneck of communication overhead that hinders scalability. In this paper, we propose a compression framework called Dynamic Communication Thresholding (DCT) for communication-efficient hybrid training. DCT filters the entities to be communicated across the network through a simple hard-thresholding function, allowing only the most relevant information to pass through. For communication efficient DP, DCT compresses the parameter gradients sent to the parameter server during model synchronization, while compensating for the introduced errors with known techniques. For communication efficient MP, DCT incorporates a novel technique to compress the activations and gradients sent across the network during the forward and backward propagation, respectively. This is done by identifying and updating only the most relevant neurons of the neural network for each training sample in the data. Under modest assumptions, we show that the convergence of training is maintained with DCT. We evaluate DCT on natural language processing and recommender system models. DCT reduces overall communication by 20x, improving end-to-end training time on industry scale models by 37%. Moreover, we observe an improvement in the trained model performance, as the induced sparsity is possibly acting as an implicit sparsity based regularization.

A Progressive Batching L-BFGS Method for Machine Learning

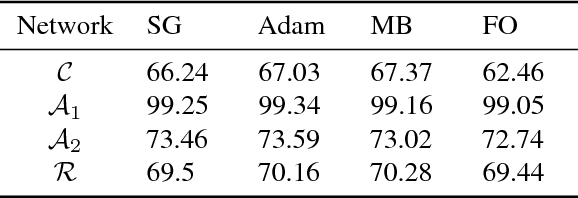
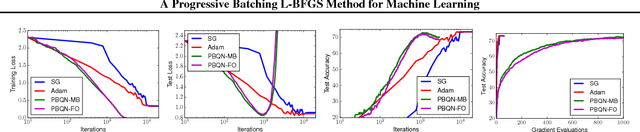
The standard L-BFGS method relies on gradient approximations that are not dominated by noise, so that search directions are descent directions, the line search is reliable, and quasi-Newton updating yields useful quadratic models of the objective function. All of this appears to call for a full batch approach, but since small batch sizes give rise to faster algorithms with better generalization properties, L-BFGS is currently not considered an algorithm of choice for large-scale machine learning applications. One need not, however, choose between the two extremes represented by the full batch or highly stochastic regimes, and may instead follow a progressive batching approach in which the sample size increases during the course of the optimization. In this paper, we present a new version of the L-BFGS algorithm that combines three basic components - progressive batching, a stochastic line search, and stable quasi-Newton updating - and that performs well on training logistic regression and deep neural networks. We provide supporting convergence theory for the method.

Dictionary Learning by Dynamical Neural Networks

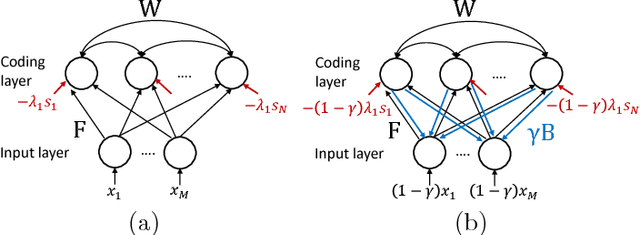
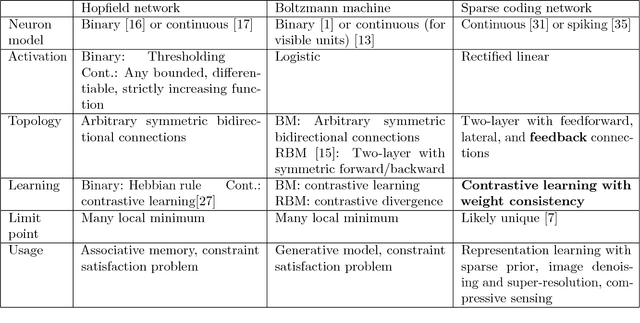
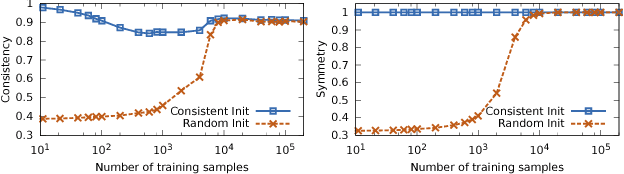
A dynamical neural network consists of a set of interconnected neurons that interact over time continuously. It can exhibit computational properties in the sense that the dynamical system's evolution and/or limit points in the associated state space can correspond to numerical solutions to certain mathematical optimization or learning problems. Such a computational system is particularly attractive in that it can be mapped to a massively parallel computer architecture for power and throughput efficiency, especially if each neuron can rely solely on local information (i.e., local memory). Deriving gradients from the dynamical network's various states while conforming to this last constraint, however, is challenging. We show that by combining ideas of top-down feedback and contrastive learning, a dynamical network for solving the l1-minimizing dictionary learning problem can be constructed, and the true gradients for learning are provably computable by individual neurons. Using spiking neurons to construct our dynamical network, we present a learning process, its rigorous mathematical analysis, and numerical results on several dictionary learning problems.

Enabling Sparse Winograd Convolution by Native Pruning

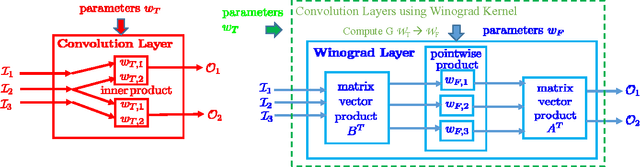
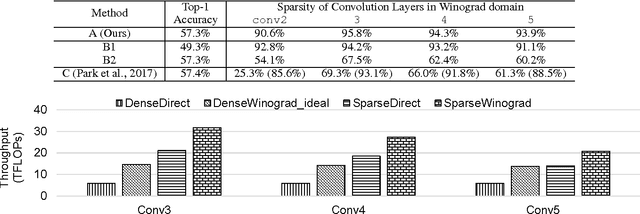
Sparse methods and the use of Winograd convolutions are two orthogonal approaches, each of which significantly accelerates convolution computations in modern CNNs. Sparse Winograd merges these two and thus has the potential to offer a combined performance benefit. Nevertheless, training convolution layers so that the resulting Winograd kernels are sparse has not hitherto been very successful. By introducing a Winograd layer in place of a standard convolution layer, we can learn and prune Winograd coefficients "natively" and obtain sparsity level beyond 90% with only 0.1% accuracy loss with AlexNet on ImageNet dataset. Furthermore, we present a sparse Winograd convolution algorithm and implementation that exploits the sparsity, achieving up to 31.7 effective TFLOP/s in 32-bit precision on a latest Intel Xeon CPU, which corresponds to a 5.4x speedup over a state-of-the-art dense convolution implementation.

Faster CNNs with Direct Sparse Convolutions and Guided Pruning

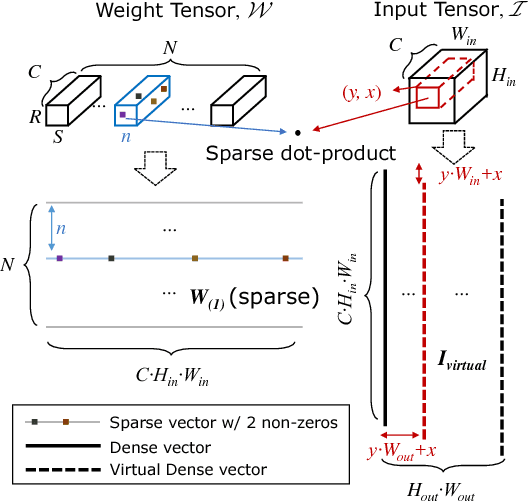
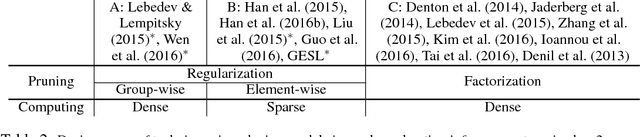
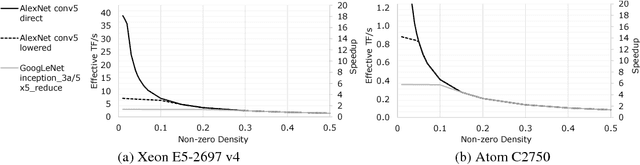
Phenomenally successful in practical inference problems, convolutional neural networks (CNN) are widely deployed in mobile devices, data centers, and even supercomputers. The number of parameters needed in CNNs, however, are often large and undesirable. Consequently, various methods have been developed to prune a CNN once it is trained. Nevertheless, the resulting CNNs offer limited benefits. While pruning the fully connected layers reduces a CNN's size considerably, it does not improve inference speed noticeably as the compute heavy parts lie in convolutions. Pruning CNNs in a way that increase inference speed often imposes specific sparsity structures, thus limiting the achievable sparsity levels. We present a method to realize simultaneously size economy and speed improvement while pruning CNNs. Paramount to our success is an efficient general sparse-with-dense matrix multiplication implementation that is applicable to convolution of feature maps with kernels of arbitrary sparsity patterns. Complementing this, we developed a performance model that predicts sweet spots of sparsity levels for different layers and on different computer architectures. Together, these two allow us to demonstrate 3.1--7.3$\times$ convolution speedups over dense convolution in AlexNet, on Intel Atom, Xeon, and Xeon Phi processors, spanning the spectrum from mobile devices to supercomputers. We also open source our project at https://github.com/IntelLabs/SkimCaffe.

Sparse Coding by Spiking Neural Networks: Convergence Theory and Computational Results

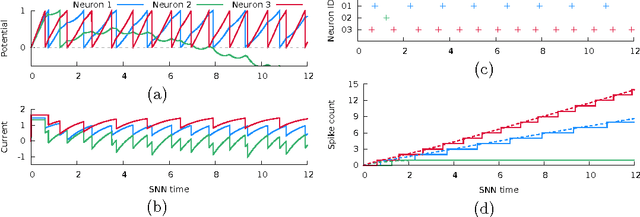
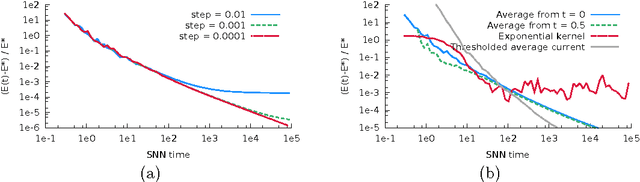
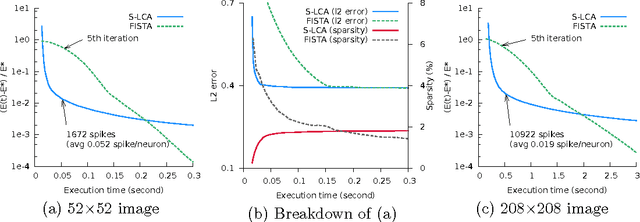
In a spiking neural network (SNN), individual neurons operate autonomously and only communicate with other neurons sparingly and asynchronously via spike signals. These characteristics render a massively parallel hardware implementation of SNN a potentially powerful computer, albeit a non von Neumann one. But can one guarantee that a SNN computer solves some important problems reliably? In this paper, we formulate a mathematical model of one SNN that can be configured for a sparse coding problem for feature extraction. With a moderate but well-defined assumption, we prove that the SNN indeed solves sparse coding. To the best of our knowledge, this is the first rigorous result of this kind.

On Large-Batch Training for Deep Learning: Generalization Gap and Sharp Minima

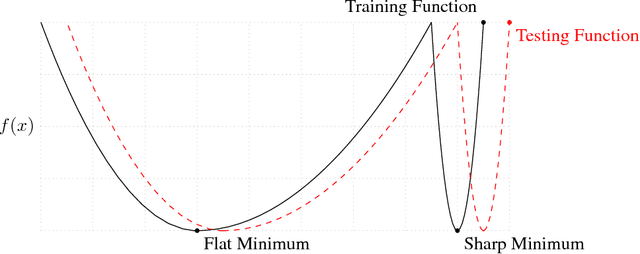
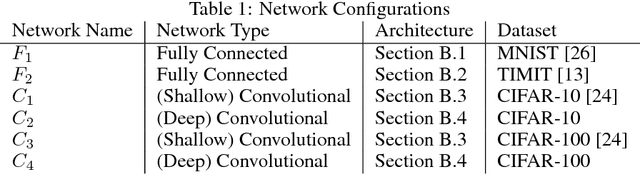
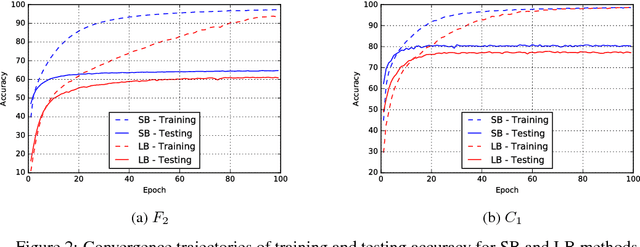
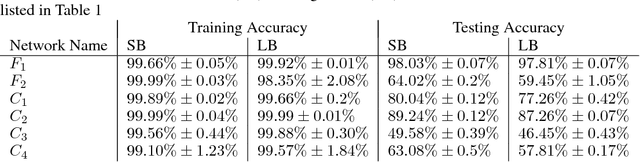
The stochastic gradient descent (SGD) method and its variants are algorithms of choice for many Deep Learning tasks. These methods operate in a small-batch regime wherein a fraction of the training data, say $32$-$512$ data points, is sampled to compute an approximation to the gradient. It has been observed in practice that when using a larger batch there is a degradation in the quality of the model, as measured by its ability to generalize. We investigate the cause for this generalization drop in the large-batch regime and present numerical evidence that supports the view that large-batch methods tend to converge to sharp minimizers of the training and testing functions - and as is well known, sharp minima lead to poorer generalization. In contrast, small-batch methods consistently converge to flat minimizers, and our experiments support a commonly held view that this is due to the inherent noise in the gradient estimation. We discuss several strategies to attempt to help large-batch methods eliminate this generalization gap.