Spectral Representation for Causal Estimation with Hidden Confounders

We address the problem of causal effect estimation where hidden confounders are present, with a focus on two settings: instrumental variable regression with additional observed confounders, and proxy causal learning. Our approach uses a singular value decomposition of a conditional expectation operator, followed by a saddle-point optimization problem, which, in the context of IV regression, can be thought of as a neural net generalization of the seminal approach due to Darolles et al. [2011]. Saddle-point formulations have gathered considerable attention recently, as they can avoid double sampling bias and are amenable to modern function approximation methods. We provide experimental validation in various settings, and show that our approach outperforms existing methods on common benchmarks.

DeepSeek-VL: Towards Real-World Vision-Language Understanding

We present DeepSeek-VL, an open-source Vision-Language (VL) Model designed for real-world vision and language understanding applications. Our approach is structured around three key dimensions: We strive to ensure our data is diverse, scalable, and extensively covers real-world scenarios including web screenshots, PDFs, OCR, charts, and knowledge-based content, aiming for a comprehensive representation of practical contexts. Further, we create a use case taxonomy from real user scenarios and construct an instruction tuning dataset accordingly. The fine-tuning with this dataset substantially improves the model's user experience in practical applications. Considering efficiency and the demands of most real-world scenarios, DeepSeek-VL incorporates a hybrid vision encoder that efficiently processes high-resolution images (1024 x 1024), while maintaining a relatively low computational overhead. This design choice ensures the model's ability to capture critical semantic and detailed information across various visual tasks. We posit that a proficient Vision-Language Model should, foremost, possess strong language abilities. To ensure the preservation of LLM capabilities during pretraining, we investigate an effective VL pretraining strategy by integrating LLM training from the beginning and carefully managing the competitive dynamics observed between vision and language modalities. The DeepSeek-VL family (both 1.3B and 7B models) showcases superior user experiences as a vision-language chatbot in real-world applications, achieving state-of-the-art or competitive performance across a wide range of visual-language benchmarks at the same model size while maintaining robust performance on language-centric benchmarks. We have made both 1.3B and 7B models publicly accessible to foster innovations based on this foundation model.

DeepSeek LLM: Scaling Open-Source Language Models with Longtermism

The rapid development of open-source large language models (LLMs) has been truly remarkable. However, the scaling law described in previous literature presents varying conclusions, which casts a dark cloud over scaling LLMs. We delve into the study of scaling laws and present our distinctive findings that facilitate scaling of large scale models in two commonly used open-source configurations, 7B and 67B. Guided by the scaling laws, we introduce DeepSeek LLM, a project dedicated to advancing open-source language models with a long-term perspective. To support the pre-training phase, we have developed a dataset that currently consists of 2 trillion tokens and is continuously expanding. We further conduct supervised fine-tuning (SFT) and Direct Preference Optimization (DPO) on DeepSeek LLM Base models, resulting in the creation of DeepSeek Chat models. Our evaluation results demonstrate that DeepSeek LLM 67B surpasses LLaMA-2 70B on various benchmarks, particularly in the domains of code, mathematics, and reasoning. Furthermore, open-ended evaluations reveal that DeepSeek LLM 67B Chat exhibits superior performance compared to GPT-3.5.

Provable Representation with Efficient Planning for Partially Observable Reinforcement Learning

In real-world reinforcement learning problems, the state information is often only partially observable, which breaks the basic assumption in Markov decision processes, and thus, leads to inferior performances. Partially Observable Markov Decision Processes have been introduced to explicitly take the issue into account for learning, exploration, and planning, but presenting significant computational and statistical challenges. To address these difficulties, we exploit the representation view, which leads to a coherent design framework for a practically tractable reinforcement learning algorithm upon partial observations. We provide a theoretical analysis for justifying the statistical efficiency of the proposed algorithm. We also empirically demonstrate the proposed algorithm can surpass state-of-the-art performance with partial observations across various benchmarks, therefore, pushing reliable reinforcement learning towards more practical applications.

Stochastic Nonlinear Control via Finite-dimensional Spectral Dynamic Embedding

Optimal control is notoriously difficult for stochastic nonlinear systems. Ren et al. introduced Spectral Dynamics Embedding for developing reinforcement learning methods for controlling an unknown system. It uses an infinite-dimensional feature to linearly represent the state-value function and exploits finite-dimensional truncation approximation for practical implementation. However, the finite-dimensional approximation properties in control have not been investigated even when the model is known. In this paper, we provide a tractable stochastic nonlinear control algorithm that exploits the nonlinear dynamics upon the finite-dimensional feature approximation, Spectral Dynamics Embedding Control (SDEC), with an in-depth theoretical analysis to characterize the approximation error induced by the finite-dimension truncation and statistical error induced by finite-sample approximation in both policy evaluation and policy optimization. We also empirically test the algorithm and compare the performance with Koopman-based methods and iLQR methods on the pendulum swingup problem.

Markovian Sliced Wasserstein Distances: Beyond Independent Projections

Sliced Wasserstein (SW) distance suffers from redundant projections due to independent uniform random projecting directions. To partially overcome the issue, max K sliced Wasserstein (Max-K-SW) distance ($K\geq 1$), seeks the best discriminative orthogonal projecting directions. Despite being able to reduce the number of projections, the metricity of Max-K-SW cannot be guaranteed in practice due to the non-optimality of the optimization. Moreover, the orthogonality constraint is also computationally expensive and might not be effective. To address the problem, we introduce a new family of SW distances, named Markovian sliced Wasserstein (MSW) distance, which imposes a first-order Markov structure on projecting directions. We discuss various members of MSW by specifying the Markov structure including the prior distribution, the transition distribution, and the burning and thinning technique. Moreover, we investigate the theoretical properties of MSW including topological properties (metricity, weak convergence, and connection to other distances), statistical properties (sample complexity, and Monte Carlo estimation error), and computational properties (computational complexity and memory complexity). Finally, we compare MSW distances with previous SW variants in various applications such as gradient flows, color transfer, and deep generative modeling to demonstrate the favorable performance of MSW.

Latent Variable Representation for Reinforcement Learning

Deep latent variable models have achieved significant empirical successes in model-based reinforcement learning (RL) due to their expressiveness in modeling complex transition dynamics. On the other hand, it remains unclear theoretically and empirically how latent variable models may facilitate learning, planning, and exploration to improve the sample efficiency of RL. In this paper, we provide a representation view of the latent variable models for state-action value functions, which allows both tractable variational learning algorithm and effective implementation of the optimism/pessimism principle in the face of uncertainty for exploration. In particular, we propose a computationally efficient planning algorithm with UCB exploration by incorporating kernel embeddings of latent variable models. Theoretically, we establish the sample complexity of the proposed approach in the online and offline settings. Empirically, we demonstrate superior performance over current state-of-the-art algorithms across various benchmarks.

Robustify Transformers with Robust Kernel Density Estimation

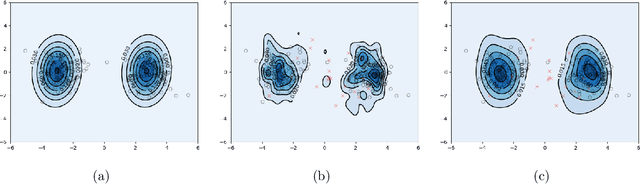
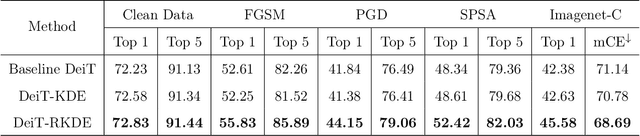
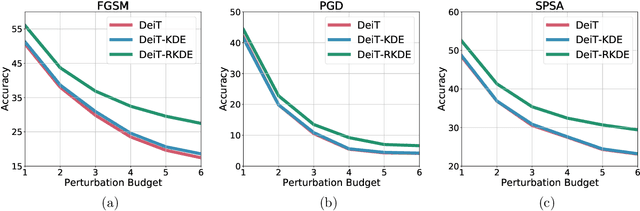
Recent advances in Transformer architecture have empowered its empirical success in various tasks across different domains. However, existing works mainly focus on improving the standard accuracy and computational cost, without considering the robustness of contaminated samples. Existing work has shown that the self-attention mechanism, which is the center of the Transformer architecture, can be viewed as a non-parametric estimator based on the well-known kernel density estimation (KDE). This motivates us to leverage the robust kernel density estimation (RKDE) in the self-attention mechanism, to alleviate the issue of the contamination of data by down-weighting the weight of bad samples in the estimation process. The modified self-attention mechanism can be incorporated into different Transformer variants. Empirical results on language modeling and image classification tasks demonstrate the effectiveness of this approach.

Hierarchical Sliced Wasserstein Distance

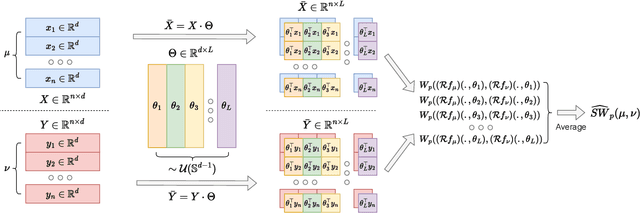
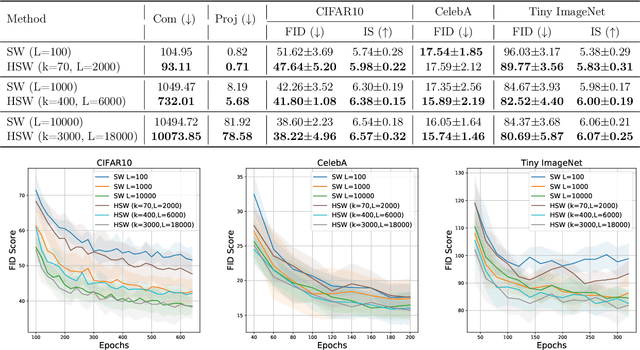
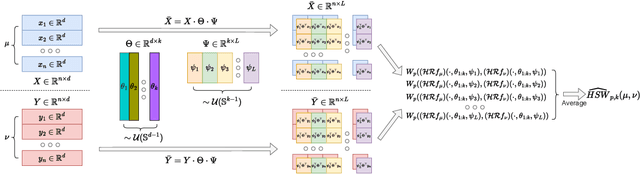
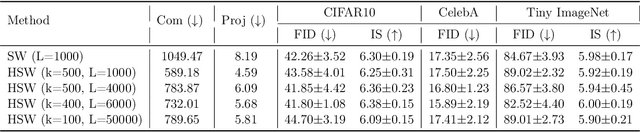
Sliced Wasserstein (SW) distance has been widely used in different application scenarios since it can be scaled to a large number of supports without suffering from the curse of dimensionality. The value of sliced Wasserstein distance is the average of transportation cost between one-dimensional representations (projections) of original measures that are obtained by Radon Transform (RT). Despite its efficiency in the number of supports, estimating the sliced Wasserstein requires a relatively large number of projections in high-dimensional settings. Therefore, for applications where the number of supports is relatively small compared with the dimension, e.g., several deep learning applications where the mini-batch approaches are utilized, the complexities from matrix multiplication of Radon Transform become the main computational bottleneck. To address this issue, we propose to derive projections by linearly and randomly combining a smaller number of projections which are named bottleneck projections. We explain the usage of these projections by introducing Hierarchical Radon Transform (HRT) which is constructed by applying Radon Transform variants recursively. We then formulate the approach into a new metric between measures, named Hierarchical Sliced Wasserstein (HSW) distance. By proving the injectivity of HRT, we derive the metricity of HSW. Moreover, we investigate the theoretical properties of HSW including its connection to SW variants and its computational and sample complexities. Finally, we compare the computational cost and generative quality of HSW with the conventional SW on the task of deep generative modeling using various benchmark datasets including CIFAR10, CelebA, and Tiny ImageNet.

Spectral Decomposition Representation for Reinforcement Learning

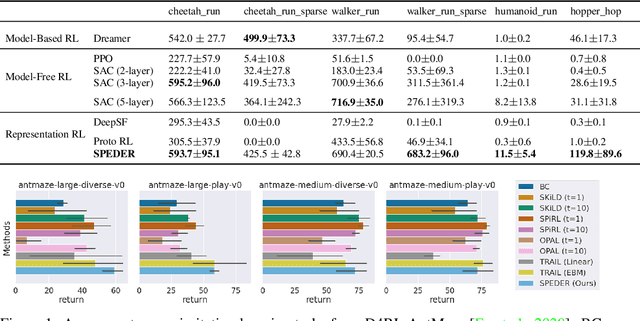
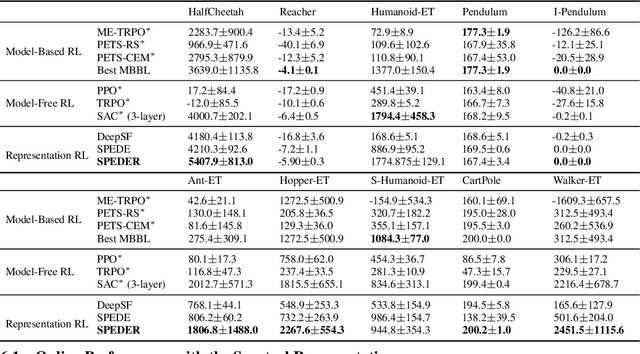
Representation learning often plays a critical role in reinforcement learning by managing the curse of dimensionality. A representative class of algorithms exploits a spectral decomposition of the stochastic transition dynamics to construct representations that enjoy strong theoretical properties in an idealized setting. However, current spectral methods suffer from limited applicability because they are constructed for state-only aggregation and derived from a policy-dependent transition kernel, without considering the issue of exploration. To address these issues, we propose an alternative spectral method, Spectral Decomposition Representation (SPEDER), that extracts a state-action abstraction from the dynamics without inducing spurious dependence on the data collection policy, while also balancing the exploration-versus-exploitation trade-off during learning. A theoretical analysis establishes the sample efficiency of the proposed algorithm in both the online and offline settings. In addition, an experimental investigation demonstrates superior performance over current state-of-the-art algorithms across several benchmarks.