Scalable spectral representations for network multiagent control

Network Markov Decision Processes (MDPs), a popular model for multi-agent control, pose a significant challenge to efficient learning due to the exponential growth of the global state-action space with the number of agents. In this work, utilizing the exponential decay property of network dynamics, we first derive scalable spectral local representations for network MDPs, which induces a network linear subspace for the local $Q$-function of each agent. Building on these local spectral representations, we design a scalable algorithmic framework for continuous state-action network MDPs, and provide end-to-end guarantees for the convergence of our algorithm. Empirically, we validate the effectiveness of our scalable representation-based approach on two benchmark problems, and demonstrate the advantages of our approach over generic function approximation approaches to representing the local $Q$-functions.

Distributed Thompson sampling under constrained communication

In Bayesian optimization, a black-box function is maximized via the use of a surrogate model. We apply distributed Thompson sampling, using a Gaussian process as a surrogate model, to approach the multi-agent Bayesian optimization problem. In our distributed Thompson sampling implementation, each agent receives sampled points from neighbors, where the communication network is encoded in a graph; each agent utilizes a Gaussian process to model the objective function. We demonstrate a theoretical bound on Bayesian Simple Regret, where the bound depends on the size of the largest complete subgraph of the communication graph. Unlike in batch Bayesian optimization, this bound is applicable in cases where the communication graph amongst agents is constrained. When compared to sequential Thompson sampling, our bound guarantees faster convergence with respect to time as long as there is a fully connected subgraph of at least two agents. We confirm the efficacy of our algorithm with numerical simulations on traditional optimization test functions, illustrating the significance of graph connectivity on improving regret convergence.

Enhancing Preference-based Linear Bandits via Human Response Time

Binary human choice feedback is widely used in interactive preference learning for its simplicity, but it provides limited information about preference strength. To overcome this limitation, we leverage human response times, which inversely correlate with preference strength, as complementary information. Our work integrates the EZ-diffusion model, which jointly models human choices and response times, into preference-based linear bandits. We introduce a computationally efficient utility estimator that reformulates the utility estimation problem using both choices and response times as a linear regression problem. Theoretical and empirical comparisons with traditional choice-only estimators reveal that for queries with strong preferences ("easy" queries), choices alone provide limited information, while response times offer valuable complementary information about preference strength. As a result, incorporating response times makes easy queries more useful. We demonstrate this advantage in the fixed-budget best-arm identification problem, with simulations based on three real-world datasets, consistently showing accelerated learning when response times are incorporated.

Skill Transfer and Discovery for Sim-to-Real Learning: A Representation-Based Viewpoint

We study sim-to-real skill transfer and discovery in the context of robotics control using representation learning. We draw inspiration from spectral decomposition of Markov decision processes. The spectral decomposition brings about representation that can linearly represent the state-action value function induced by any policies, thus can be regarded as skills. The skill representations are transferable across arbitrary tasks with the same transition dynamics. Moreover, to handle the sim-to-real gap in the dynamics, we propose a skill discovery algorithm that learns new skills caused by the sim-to-real gap from real-world data. We promote the discovery of new skills by enforcing orthogonal constraints between the skills to learn and the skills from simulators, and then synthesize the policy using the enlarged skill sets. We demonstrate our methodology by transferring quadrotor controllers from simulators to Crazyflie 2.1 quadrotors. We show that we can learn the skill representations from a single simulator task and transfer these to multiple different real-world tasks including hovering, taking off, landing and trajectory tracking. Our skill discovery approach helps narrow the sim-to-real gap and improve the real-world controller performance by up to 30.2%.

Minimizing the Thompson Sampling Regret-to-Sigma Ratio (TS-RSR): a provably efficient algorithm for batch Bayesian Optimization

This paper presents a new approach for batch Bayesian Optimization (BO), where the sampling takes place by minimizing a Thompson Sampling approximation of a regret to uncertainty ratio. Our objective is able to coordinate the actions chosen in each batch in a way that minimizes redundancy between points whilst focusing on points with high predictive means or high uncertainty. We provide high-probability theoretical guarantees on the regret of our algorithm. Finally, numerically, we demonstrate that our method attains state-of-the-art performance on a range of nonconvex test functions, where it outperforms several competitive benchmark batch BO algorithms by an order of magnitude on average.

Stochastic Nonlinear Control via Finite-dimensional Spectral Dynamic Embedding

Optimal control is notoriously difficult for stochastic nonlinear systems. Ren et al. introduced Spectral Dynamics Embedding for developing reinforcement learning methods for controlling an unknown system. It uses an infinite-dimensional feature to linearly represent the state-value function and exploits finite-dimensional truncation approximation for practical implementation. However, the finite-dimensional approximation properties in control have not been investigated even when the model is known. In this paper, we provide a tractable stochastic nonlinear control algorithm that exploits the nonlinear dynamics upon the finite-dimensional feature approximation, Spectral Dynamics Embedding Control (SDEC), with an in-depth theoretical analysis to characterize the approximation error induced by the finite-dimension truncation and statistical error induced by finite-sample approximation in both policy evaluation and policy optimization. We also empirically test the algorithm and compare the performance with Koopman-based methods and iLQR methods on the pendulum swingup problem.

FedDAR: Federated Domain-Aware Representation Learning

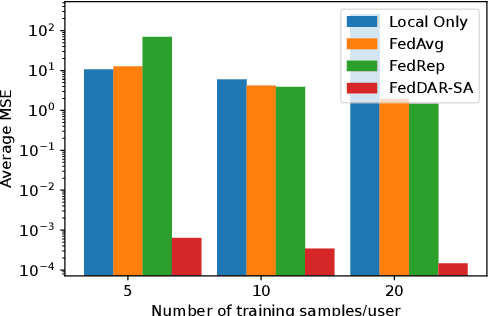
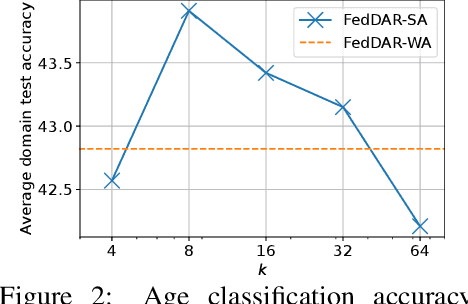
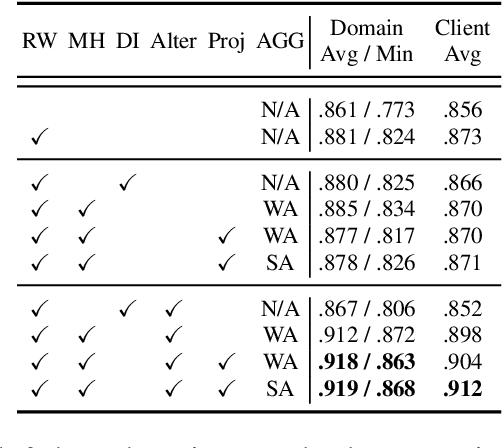
Cross-silo Federated learning (FL) has become a promising tool in machine learning applications for healthcare. It allows hospitals/institutions to train models with sufficient data while the data is kept private. To make sure the FL model is robust when facing heterogeneous data among FL clients, most efforts focus on personalizing models for clients. However, the latent relationships between clients' data are ignored. In this work, we focus on a special non-iid FL problem, called Domain-mixed FL, where each client's data distribution is assumed to be a mixture of several predefined domains. Recognizing the diversity of domains and the similarity within domains, we propose a novel method, FedDAR, which learns a domain shared representation and domain-wise personalized prediction heads in a decoupled manner. For simplified linear regression settings, we have theoretically proved that FedDAR enjoys a linear convergence rate. For general settings, we have performed intensive empirical studies on both synthetic and real-world medical datasets which demonstrate its superiority over prior FL methods.

Gradient Play in Multi-Agent Markov Stochastic Games: Stationary Points and Convergence

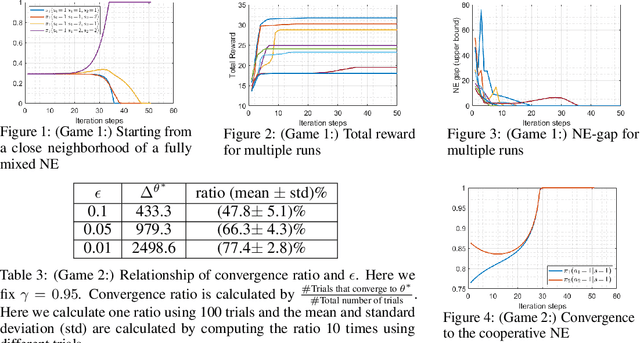
We study the performance of the gradient play algorithm for multi-agent tabular Markov decision processes (MDPs), which are also known as stochastic games (SGs), where each agent tries to maximize its own total discounted reward by making decisions independently based on current state information which is shared between agents. Policies are directly parameterized by the probability of choosing a certain action at a given state. We show that Nash equilibria (NEs) and first order stationary policies are equivalent in this setting, and give a non-asymptotic global convergence rate analysis to an $\epsilon$-NE for a subclass of multi-agent MDPs called Markov potential games, which includes the cooperative setting with identical rewards among agents as an important special case. Our result shows that the number of iterations to reach an $\epsilon$-NE scales linearly, instead of exponentially, with the number of agents. Local geometry and local stability are also considered. For Markov potential games, we prove that strict NEs are local maxima of the total potential function and fully-mixed NEs are saddle points. We also give a local convergence rate around strict NEs for more general settings.

Federated LQR: Learning through Sharing

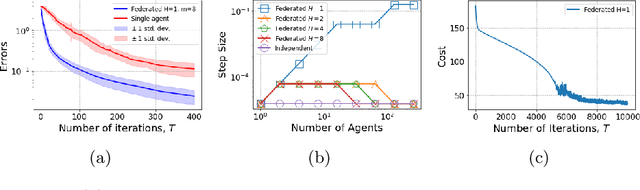
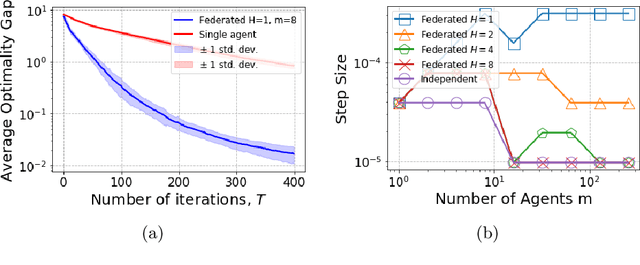
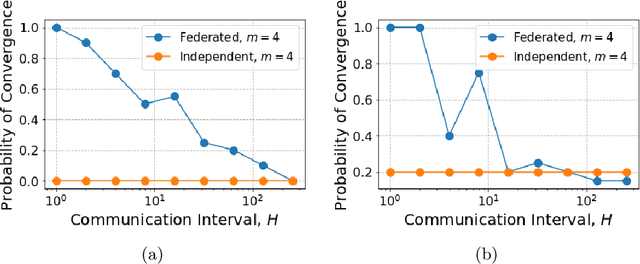
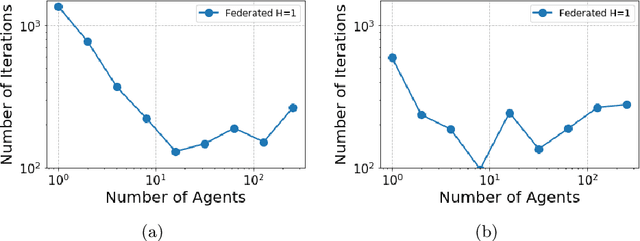
In many multi-agent reinforcement learning applications such as flocking, multi-robot applications and smart manufacturing, distinct agents share similar dynamics but face different objectives. In these applications, an important question is how the similarities amongst the agents can accelerate learning in spite of the agents' differing goals. We study a distributed LQR (Linear Quadratic Regulator) tracking problem which models this setting, where the agents, acting independently, share identical (unknown) dynamics and cost structure but need to track different targets. In this paper, we propose a communication-efficient, federated model-free zeroth-order algorithm that provably achieves a convergence speedup linear in the number of agents compared with the communication-free setup where each agent's problem is treated independently. We support our arguments with numerical simulations of both linear and nonlinear systems.