Unified Local and Global Attention Interaction Modeling for Vision Transformers

We present a novel method that extends the self-attention mechanism of a vision transformer (ViT) for more accurate object detection across diverse datasets. ViTs show strong capability for image understanding tasks such as object detection, segmentation, and classification. This is due in part to their ability to leverage global information from interactions among visual tokens. However, the self-attention mechanism in ViTs are limited because they do not allow visual tokens to exchange local or global information with neighboring features before computing global attention. This is problematic because tokens are treated in isolation when attending (matching) to other tokens, and valuable spatial relationships are overlooked. This isolation is further compounded by dot-product similarity operations that make tokens from different semantic classes appear visually similar. To address these limitations, we introduce two modifications to the traditional self-attention framework; a novel aggressive convolution pooling strategy for local feature mixing, and a new conceptual attention transformation to facilitate interaction and feature exchange between semantic concepts. Experimental results demonstrate that local and global information exchange among visual features before self-attention significantly improves performance on challenging object detection tasks and generalizes across multiple benchmark datasets and challenging medical datasets. We publish source code and a novel dataset of cancerous tumors (chimeric cell clusters).

Neural Collapse for Cross-entropy Class-Imbalanced Learning with Unconstrained ReLU Feature Model

The current paradigm of training deep neural networks for classification tasks includes minimizing the empirical risk that pushes the training loss value towards zero, even after the training error has been vanished. In this terminal phase of training, it has been observed that the last-layer features collapse to their class-means and these class-means converge to the vertices of a simplex Equiangular Tight Frame (ETF). This phenomenon is termed as Neural Collapse (NC). To theoretically understand this phenomenon, recent works employ a simplified unconstrained feature model to prove that NC emerges at the global solutions of the training problem. However, when the training dataset is class-imbalanced, some NC properties will no longer be true. For example, the class-means geometry will skew away from the simplex ETF when the loss converges. In this paper, we generalize NC to imbalanced regime for cross-entropy loss under the unconstrained ReLU feature model. We prove that, while the within-class features collapse property still holds in this setting, the class-means will converge to a structure consisting of orthogonal vectors with different lengths. Furthermore, we find that the classifier weights are aligned to the scaled and centered class-means with scaling factors depend on the number of training samples of each class, which generalizes NC in the class-balanced setting. We empirically prove our results through experiments on practical architectures and dataset.

Unveiling Comparative Sentiments in Vietnamese Product Reviews: A Sequential Classification Framework

Comparative opinion mining is a specialized field of sentiment analysis that aims to identify and extract sentiments expressed comparatively. To address this task, we propose an approach that consists of solving three sequential sub-tasks: (i) identifying comparative sentence, i.e., if a sentence has a comparative meaning, (ii) extracting comparative elements, i.e., what are comparison subjects, objects, aspects, predicates, and (iii) classifying comparison types which contribute to a deeper comprehension of user sentiments in Vietnamese product reviews. Our method is ranked fifth at the Vietnamese Language and Speech Processing (VLSP) 2023 challenge on Comparative Opinion Mining (ComOM) from Vietnamese Product Reviews.

Touch, press and stroke: a soft capacitive sensor skin

Soft sensors that can discriminate shear and normal force could help provide machines the fine control desirable for safe and effective physical interactions with people. A capacitive sensor is made for this purpose, composed of patterned elastomer and containing both fixed and sliding pillars that allow the sensor to deform and buckle, much like skin itself. The sensor differentiates between simultaneously applied pressure and shear. In addition, finger proximity is detectable up to 15 mm, with a pressure and shear sensitivity of 1 kPa and a displacement resolution of 50 $\mu$m. The operation is demonstrated on a simple gripper holding a cup. The combination of features and the straightforward fabrication method make this sensor a candidate for implementation as a sensing skin for humanoid robotics applications.

Posterior Collapse in Linear Conditional and Hierarchical Variational Autoencoders

The posterior collapse phenomenon in variational autoencoders (VAEs), where the variational posterior distribution closely matches the prior distribution, can hinder the quality of the learned latent variables. As a consequence of posterior collapse, the latent variables extracted by the encoder in VAEs preserve less information from the input data and thus fail to produce meaningful representations as input to the reconstruction process in the decoder. While this phenomenon has been an actively addressed topic related to VAEs performance, the theory for posterior collapse remains underdeveloped, especially beyond the standard VAEs. In this work, we advance the theoretical understanding of posterior collapse to two important and prevalent yet less studied classes of VAEs: conditional VAEs and hierarchical VAEs. Specifically, via a non-trivial theoretical analysis of linear conditional VAEs and hierarchical VAEs with two levels of latent, we prove that the cause of posterior collapses in these models includes the correlation between the input and output of the conditional VAEs and the effect of learnable encoder variance in the hierarchical VAEs. We empirically validate our theoretical findings for linear conditional and hierarchical VAEs and demonstrate that these results are also predictive for non-linear cases.

Neural Collapse in Deep Linear Network: From Balanced to Imbalanced Data

Modern deep neural networks have achieved superhuman performance in tasks from image classification to game play. Surprisingly, these various complex systems with massive amounts of parameters exhibit the same remarkable structural properties in their last-layer features and classifiers across canonical datasets. This phenomenon is known as "Neural Collapse," and it was discovered empirically by Papyan et al. \cite{Papyan20}. Recent papers have theoretically shown the global solutions to the training network problem under a simplified "unconstrained feature model" exhibiting this phenomenon. We take a step further and prove the Neural Collapse occurrence for deep linear network for the popular mean squared error (MSE) and cross entropy (CE) loss. Furthermore, we extend our research to imbalanced data for MSE loss and present the first geometric analysis for Neural Collapse under this setting.

Revisiting Over-smoothing and Over-squashing using Ollivier's Ricci Curvature

Graph Neural Networks (GNNs) had been demonstrated to be inherently susceptible to the problems of over-smoothing and over-squashing. These issues prohibit the ability of GNNs to model complex graph interactions by limiting their effectiveness at taking into account distant information. Our study reveals the key connection between the local graph geometry and the occurrence of both of these issues, thereby providing a unified framework for studying them at a local scale using the Ollivier's Ricci curvature. Based on our theory, a number of principled methods are proposed to alleviate the over-smoothing and over-squashing issues.

Hierarchical Sliced Wasserstein Distance

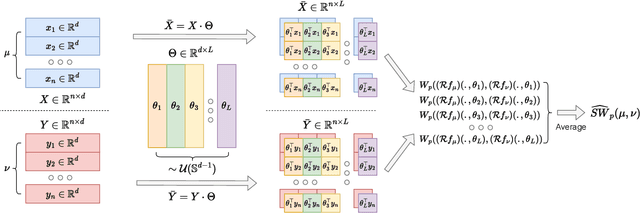
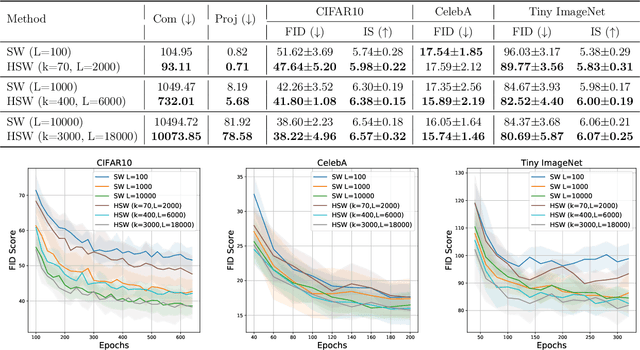
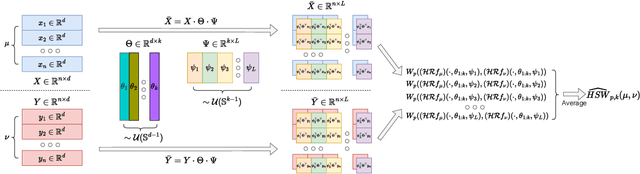
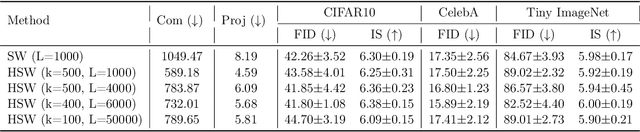
Sliced Wasserstein (SW) distance has been widely used in different application scenarios since it can be scaled to a large number of supports without suffering from the curse of dimensionality. The value of sliced Wasserstein distance is the average of transportation cost between one-dimensional representations (projections) of original measures that are obtained by Radon Transform (RT). Despite its efficiency in the number of supports, estimating the sliced Wasserstein requires a relatively large number of projections in high-dimensional settings. Therefore, for applications where the number of supports is relatively small compared with the dimension, e.g., several deep learning applications where the mini-batch approaches are utilized, the complexities from matrix multiplication of Radon Transform become the main computational bottleneck. To address this issue, we propose to derive projections by linearly and randomly combining a smaller number of projections which are named bottleneck projections. We explain the usage of these projections by introducing Hierarchical Radon Transform (HRT) which is constructed by applying Radon Transform variants recursively. We then formulate the approach into a new metric between measures, named Hierarchical Sliced Wasserstein (HSW) distance. By proving the injectivity of HRT, we derive the metricity of HSW. Moreover, we investigate the theoretical properties of HSW including its connection to SW variants and its computational and sample complexities. Finally, we compare the computational cost and generative quality of HSW with the conventional SW on the task of deep generative modeling using various benchmark datasets including CIFAR10, CelebA, and Tiny ImageNet.

Improving Generative Flow Networks with Path Regularization

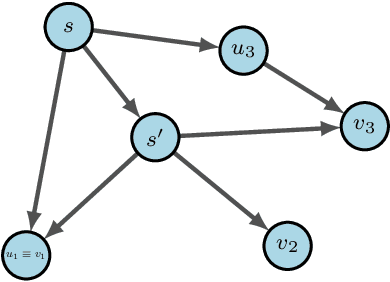
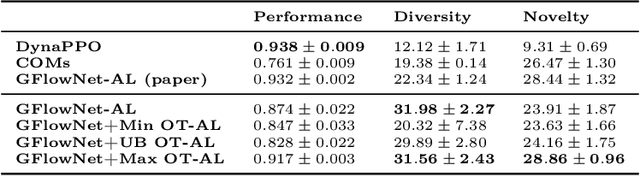
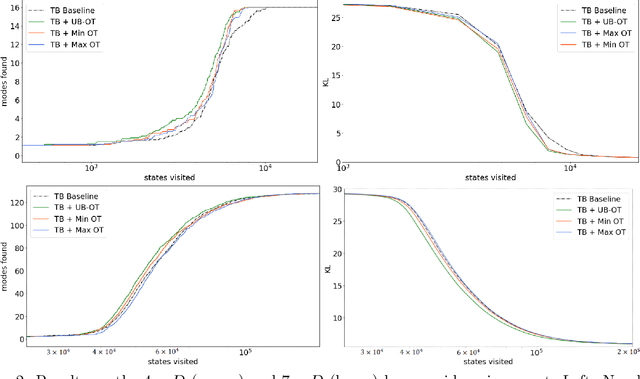
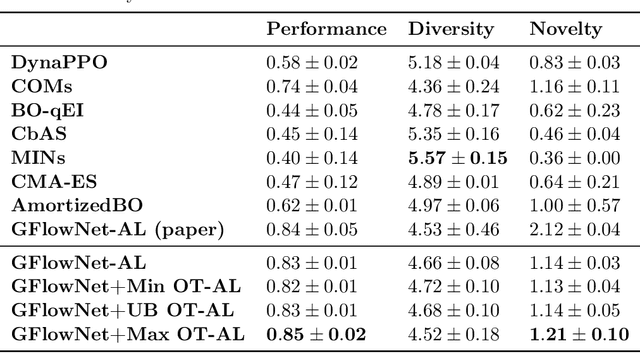
Generative Flow Networks (GFlowNets) are recently proposed models for learning stochastic policies that generate compositional objects by sequences of actions with the probability proportional to a given reward function. The central problem of GFlowNets is to improve their exploration and generalization. In this work, we propose a novel path regularization method based on optimal transport theory that places prior constraints on the underlying structure of the GFlowNets. The prior is designed to help the GFlowNets better discover the latent structure of the target distribution or enhance its ability to explore the environment in the context of active learning. The path regularization controls the flow in GFlowNets to generate more diverse and novel candidates via maximizing the optimal transport distances between two forward policies or to improve the generalization via minimizing the optimal transport distances. In addition, we derive an efficient implementation of the regularization by finding its closed form solutions in specific cases and a meaningful upper bound that can be used as an approximation to minimize the regularization term. We empirically demonstrate the advantage of our path regularization on a wide range of tasks, including synthetic hypergrid environment modeling, discrete probabilistic modeling, and biological sequence design.

Momentum Transformer: Closing the Performance Gap Between Self-attention and Its Linearization

Transformers have achieved remarkable success in sequence modeling and beyond but suffer from quadratic computational and memory complexities with respect to the length of the input sequence. Leveraging techniques include sparse and linear attention and hashing tricks; efficient transformers have been proposed to reduce the quadratic complexity of transformers but significantly degrade the accuracy. In response, we first interpret the linear attention and residual connections in computing the attention map as gradient descent steps. We then introduce momentum into these components and propose the \emph{momentum transformer}, which utilizes momentum to improve the accuracy of linear transformers while maintaining linear memory and computational complexities. Furthermore, we develop an adaptive strategy to compute the momentum value for our model based on the optimal momentum for quadratic optimization. This adaptive momentum eliminates the need to search for the optimal momentum value and further enhances the performance of the momentum transformer. A range of experiments on both autoregressive and non-autoregressive tasks, including image generation and machine translation, demonstrate that the momentum transformer outperforms popular linear transformers in training efficiency and accuracy.