DoRAN: Stabilizing Weight-Decomposed Low-Rank Adaptation via Noise Injection and Auxiliary Networks

Parameter-efficient fine-tuning (PEFT) methods have become the standard paradigm for adapting large-scale models. Among these techniques, Weight-Decomposed Low-Rank Adaptation (DoRA) has been shown to improve both the learning capacity and training stability of the vanilla Low-Rank Adaptation (LoRA) method by explicitly decomposing pre-trained weights into magnitude and directional components. In this work, we propose DoRAN, a new variant of DoRA designed to further stabilize training and boost the sample efficiency of DoRA. Our approach includes two key stages: (i) injecting noise into the denominator of DoRA's weight decomposition, which serves as an adaptive regularizer to mitigate instabilities; and (ii) replacing static low-rank matrices with auxiliary networks that generate them dynamically, enabling parameter coupling across layers and yielding better sample efficiency in both theory and practice. Comprehensive experiments on vision and language benchmarks show that DoRAN consistently outperforms LoRA, DoRA, and other PEFT baselines. These results underscore the effectiveness of combining stabilization through noise-based regularization with network-based parameter generation, offering a promising direction for robust and efficient fine-tuning of foundation models.

HoRA: Cross-Head Low-Rank Adaptation with Joint Hypernetworks

Low-Rank Adaptation (LoRA) is a parameter-efficient fine-tuning (PEFT) technique that adapts large pre-trained models by adding low-rank matrices to their weight updates. However, in the context of fine-tuning multi-head self-attention (MHA), LoRA has been employed to adapt each attention head separately, thereby overlooking potential synergies across different heads. To mitigate this issue, we propose a novel Hyper-shared Low-Rank Adaptation (HoRA) method, which utilizes joint hypernetworks to generate low-rank matrices across attention heads. By coupling their adaptation through a shared generator, HoRA encourages cross-head information sharing, and thus directly addresses the aforementioned limitation of LoRA. By comparing LoRA and HoRA through the lens of hierarchical mixture of experts, our theoretical findings reveal that the latter achieves superior sample efficiency to the former. Furthermore, through extensive experiments across diverse language and vision benchmarks, we demonstrate that HoRA outperforms LoRA and other PEFT methods while requiring only a marginal increase in the number of trainable parameters.

AG-VPReID.VIR: Bridging Aerial and Ground Platforms for Video-based Visible-Infrared Person Re-ID

Person re-identification (Re-ID) across visible and infrared modalities is crucial for 24-hour surveillance systems, but existing datasets primarily focus on ground-level perspectives. While ground-based IR systems offer nighttime capabilities, they suffer from occlusions, limited coverage, and vulnerability to obstructions--problems that aerial perspectives uniquely solve. To address these limitations, we introduce AG-VPReID.VIR, the first aerial-ground cross-modality video-based person Re-ID dataset. This dataset captures 1,837 identities across 4,861 tracklets (124,855 frames) using both UAV-mounted and fixed CCTV cameras in RGB and infrared modalities. AG-VPReID.VIR presents unique challenges including cross-viewpoint variations, modality discrepancies, and temporal dynamics. Additionally, we propose TCC-VPReID, a novel three-stream architecture designed to address the joint challenges of cross-platform and cross-modality person Re-ID. Our approach bridges the domain gaps between aerial-ground perspectives and RGB-IR modalities, through style-robust feature learning, memory-based cross-view adaptation, and intermediary-guided temporal modeling. Experiments show that AG-VPReID.VIR presents distinctive challenges compared to existing datasets, with our TCC-VPReID framework achieving significant performance gains across multiple evaluation protocols. Dataset and code are available at https://github.com/agvpreid25/AG-VPReID.VIR.

On Minimax Estimation of Parameters in Softmax-Contaminated Mixture of Experts

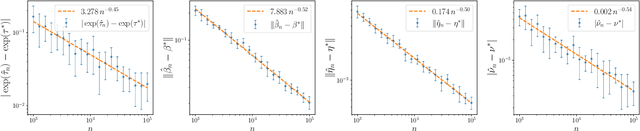
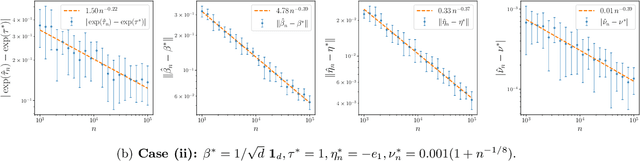
The softmax-contaminated mixture of experts (MoE) model is deployed when a large-scale pre-trained model, which plays the role of a fixed expert, is fine-tuned for learning downstream tasks by including a new contamination part, or prompt, functioning as a new, trainable expert. Despite its popularity and relevance, the theoretical properties of the softmax-contaminated MoE have remained unexplored in the literature. In the paper, we study the convergence rates of the maximum likelihood estimator of gating and prompt parameters in order to gain insights into the statistical properties and potential challenges of fine-tuning with a new prompt. We find that the estimability of these parameters is compromised when the prompt acquires overlapping knowledge with the pre-trained model, in the sense that we make precise by formulating a novel analytic notion of distinguishability. Under distinguishability of the pre-trained and prompt models, we derive minimax optimal estimation rates for all the gating and prompt parameters. By contrast, when the distinguishability condition is violated, these estimation rates become significantly slower due to their dependence on the prompt convergence rate to the pre-trained model. Finally, we empirically corroborate our theoretical findings through several numerical experiments.

CompeteSMoE -- Statistically Guaranteed Mixture of Experts Training via Competition

Sparse mixture of experts (SMoE) offers an appealing solution to scale up the model complexity beyond the mean of increasing the network's depth or width. However, we argue that effective SMoE training remains challenging because of the suboptimal routing process where experts that perform computation do not directly contribute to the routing process. In this work, we propose competition, a novel mechanism to route tokens to experts with the highest neural response. Theoretically, we show that the competition mechanism enjoys a better sample efficiency than the traditional softmax routing. Furthermore, we develop CompeteSMoE, a simple yet effective algorithm to train large language models by deploying a router to learn the competition policy, thus enjoying strong performances at a low training overhead. Our extensive empirical evaluations on both the visual instruction tuning and language pre-training tasks demonstrate the efficacy, robustness, and scalability of CompeteSMoE compared to state-of-the-art SMoE strategies. We have made the implementation available at: https://github.com/Fsoft-AIC/CompeteSMoE. This work is an improved version of the previous study at arXiv:2402.02526

On DeepSeekMoE: Statistical Benefits of Shared Experts and Normalized Sigmoid Gating

Mixture of experts (MoE) methods are a key component in most large language model architectures, including the recent series of DeepSeek models. Compared to other MoE implementations, DeepSeekMoE stands out because of two unique features: the deployment of a shared expert strategy and of the normalized sigmoid gating mechanism. Despite the prominent role of DeepSeekMoE in the success of the DeepSeek series of models, there have been only a few attempts to justify theoretically the value of the shared expert strategy, while its normalized sigmoid gating has remained unexplored. To bridge this gap, we undertake a comprehensive theoretical study of these two features of DeepSeekMoE from a statistical perspective. We perform a convergence analysis of the expert estimation task to highlight the gains in sample efficiency for both the shared expert strategy and the normalized sigmoid gating, offering useful insights into the design of expert and gating structures. To verify empirically our theoretical findings, we carry out several experiments on both synthetic data and real-world datasets for (vision) language modeling tasks. Finally, we conduct an extensive empirical analysis of the router behaviors, ranging from router saturation, router change rate, to expert utilization.

AG-VPReID: A Challenging Large-Scale Benchmark for Aerial-Ground Video-based Person Re-Identification

We introduce AG-VPReID, a challenging large-scale benchmark dataset for aerial-ground video-based person re-identification (ReID), comprising 6,632 identities, 32,321 tracklets, and 9.6 million frames captured from drones (15-120m altitude), CCTV, and wearable cameras. This dataset presents a real-world benchmark to investigate the robustness of Person ReID approaches against the unique challenges of cross-platform aerial-ground settings. To address these challenges, we propose AG-VPReID-Net, an end-to-end framework combining three complementary streams: (1) an Adapted Temporal-Spatial Stream addressing motion pattern inconsistencies and temporal feature learning, (2) a Normalized Appearance Stream using physics-informed techniques to tackle resolution and appearance changes, and (3) a Multi-Scale Attention Stream handling scale variations across drone altitudes. Our approach integrates complementary visual-semantic information from all streams to generate robust, viewpoint-invariant person representations. Extensive experiments demonstrate that AG-VPReID-Net outperforms state-of-the-art approaches on both our new dataset and other existing video-based ReID benchmarks, showcasing its effectiveness and generalizability. The relatively lower performance of all state-of-the-art approaches, including our proposed approach, on our new dataset highlights its challenging nature. The AG-VPReID dataset, code and models are available at https://github.com/agvpreid25/AG-VPReID-Net.

Convergence Rates for Softmax Gating Mixture of Experts

Mixture of experts (MoE) has recently emerged as an effective framework to advance the efficiency and scalability of machine learning models by softly dividing complex tasks among multiple specialized sub-models termed experts. Central to the success of MoE is an adaptive softmax gating mechanism which takes responsibility for determining the relevance of each expert to a given input and then dynamically assigning experts their respective weights. Despite its widespread use in practice, a comprehensive study on the effects of the softmax gating on the MoE has been lacking in the literature. To bridge this gap in this paper, we perform a convergence analysis of parameter estimation and expert estimation under the MoE equipped with the standard softmax gating or its variants, including a dense-to-sparse gating and a hierarchical softmax gating, respectively. Furthermore, our theories also provide useful insights into the design of sample-efficient expert structures. In particular, we demonstrate that it requires polynomially many data points to estimate experts satisfying our proposed \emph{strong identifiability} condition, namely a commonly used two-layer feed-forward network. In stark contrast, estimating linear experts, which violate the strong identifiability condition, necessitates exponentially many data points as a result of intrinsic parameter interactions expressed in the language of partial differential equations. All the theoretical results are substantiated with a rigorous guarantee.

On Zero-Initialized Attention: Optimal Prompt and Gating Factor Estimation

The LLaMA-Adapter has recently emerged as an efficient fine-tuning technique for LLaMA models, leveraging zero-initialized attention to stabilize training and enhance performance. However, despite its empirical success, the theoretical foundations of zero-initialized attention remain largely unexplored. In this paper, we provide a rigorous theoretical analysis, establishing a connection between zero-initialized attention and mixture-of-expert models. We prove that both linear and non-linear prompts, along with gating functions, can be optimally estimated, with non-linear prompts offering greater flexibility for future applications. Empirically, we validate our findings on the open LLM benchmarks, demonstrating that non-linear prompts outperform linear ones. Notably, even with limited training data, both prompt types consistently surpass vanilla attention, highlighting the robustness and adaptability of zero-initialized attention.

RepLoRA: Reparameterizing Low-Rank Adaptation via the Perspective of Mixture of Experts

Low-rank adaptation (LoRA) has emerged as a powerful method for fine-tuning large-scale foundation models. Despite its popularity, the theoretical understanding of LoRA has remained limited. This paper presents a theoretical analysis of LoRA by examining its connection to the Mixture of Experts models. Under this framework, we show that simple reparameterizations of the LoRA matrices can notably accelerate the low-rank matrix estimation process. In particular, we prove that reparameterization can reduce the data needed to achieve a desired estimation error from an exponential to a polynomial scale. Motivated by this insight, we propose Reparameterized Low-rank Adaptation (RepLoRA), which incorporates lightweight MLPs to reparameterize the LoRA matrices. Extensive experiments across multiple domains demonstrate that RepLoRA consistently outperforms vanilla LoRA. Notably, with limited data, RepLoRA surpasses LoRA by a margin of up to 40.0% and achieves LoRA's performance with only 30.0% of the training data, highlighting both the theoretical and empirical robustness of our PEFT method.