Roy Frostig
Learning Model Predictive Controllers with Real-Time Attention for Real-World Navigation
Sep 24, 2022
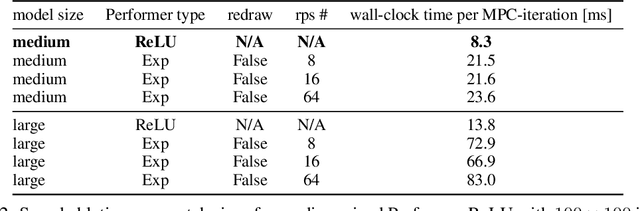


Abstract:Despite decades of research, existing navigation systems still face real-world challenges when deployed in the wild, e.g., in cluttered home environments or in human-occupied public spaces. To address this, we present a new class of implicit control policies combining the benefits of imitation learning with the robust handling of system constraints from Model Predictive Control (MPC). Our approach, called Performer-MPC, uses a learned cost function parameterized by vision context embeddings provided by Performers -- a low-rank implicit-attention Transformer. We jointly train the cost function and construct the controller relying on it, effectively solving end-to-end the corresponding bi-level optimization problem. We show that the resulting policy improves standard MPC performance by leveraging a few expert demonstrations of the desired navigation behavior in different challenging real-world scenarios. Compared with a standard MPC policy, Performer-MPC achieves >40% better goal reached in cluttered environments and >65% better on social metrics when navigating around humans.
Learning from many trajectories
Mar 31, 2022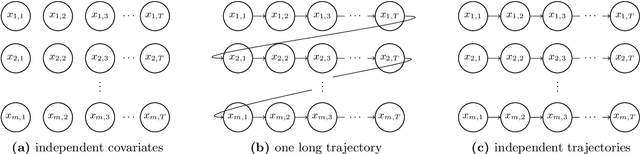
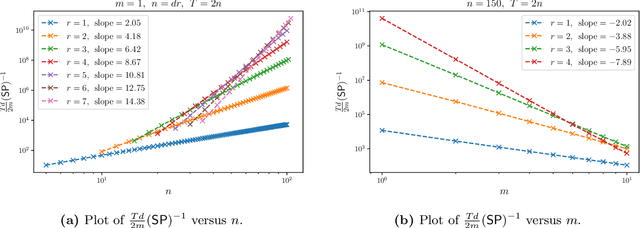
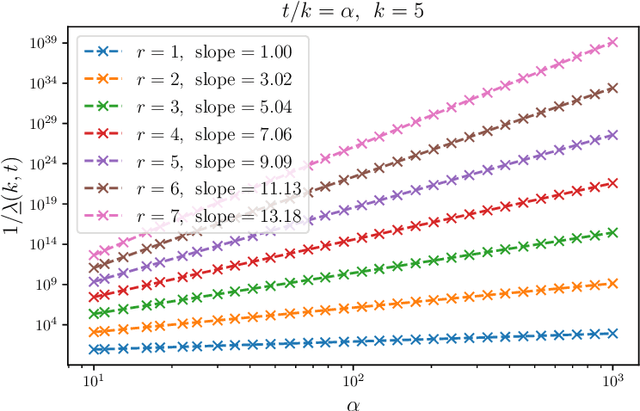
Abstract:We initiate a study of supervised learning from many independent sequences ("trajectories") of non-independent covariates, reflecting tasks in sequence modeling, control, and reinforcement learning. Conceptually, our multi-trajectory setup sits between two traditional settings in statistical learning theory: learning from independent examples and learning from a single auto-correlated sequence. Our conditions for efficient learning generalize the former setting--trajectories must be non-degenerate in ways that extend standard requirements for independent examples. They do not require that trajectories be ergodic, long, nor strictly stable. For linear least-squares regression, given $n$-dimensional examples produced by $m$ trajectories, each of length $T$, we observe a notable change in statistical efficiency as the number of trajectories increases from a few (namely $m \lesssim n$) to many (namely $m \gtrsim n$). Specifically, we establish that the worst-case error rate this problem is $\Theta(n / m T)$ whenever $m \gtrsim n$. Meanwhile, when $m \lesssim n$, we establish a (sharp) lower bound of $\Omega(n^2 / m^2 T)$ on the worst-case error rate, realized by a simple, marginally unstable linear dynamical system. A key upshot is that, in domains where trajectories regularly reset, the error rate eventually behaves as if all of the examples were independent altogether, drawn from their marginals. As a corollary of our analysis, we also improve guarantees for the linear system identification problem.
Efficient and Modular Implicit Differentiation
May 31, 2021

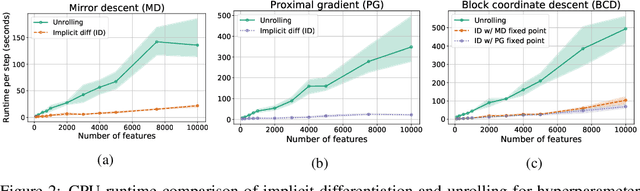

Abstract:Automatic differentiation (autodiff) has revolutionized machine learning. It allows expressing complex computations by composing elementary ones in creative ways and removes the burden of computing their derivatives by hand. More recently, differentiation of optimization problem solutions has attracted widespread attention with applications such as optimization as a layer, and in bi-level problems such as hyper-parameter optimization and meta-learning. However, the formulas for these derivatives often involve case-by-case tedious mathematical derivations. In this paper, we propose a unified, efficient and modular approach for implicit differentiation of optimization problems. In our approach, the user defines (in Python in the case of our implementation) a function $F$ capturing the optimality conditions of the problem to be differentiated. Once this is done, we leverage autodiff of $F$ and implicit differentiation to automatically differentiate the optimization problem. Our approach thus combines the benefits of implicit differentiation and autodiff. It is efficient as it can be added on top of any state-of-the-art solver and modular as the optimality condition specification is decoupled from the implicit differentiation mechanism. We show that seemingly simple principles allow to recover many recently proposed implicit differentiation methods and create new ones easily. We demonstrate the ease of formulating and solving bi-level optimization problems using our framework. We also showcase an application to the sensitivity analysis of molecular dynamics.
Decomposing reverse-mode automatic differentiation
May 20, 2021Abstract:We decompose reverse-mode automatic differentiation into (forward-mode) linearization followed by transposition. Doing so isolates the essential difference between forward- and reverse-mode AD, and simplifies their joint implementation. In particular, once forward-mode AD rules are defined for every primitive operation in a source language, only linear primitives require an additional transposition rule in order to arrive at a complete reverse-mode AD implementation. This is how reverse-mode AD is written in JAX and Dex.
The advantages of multiple classes for reducing overfitting from test set reuse
May 24, 2019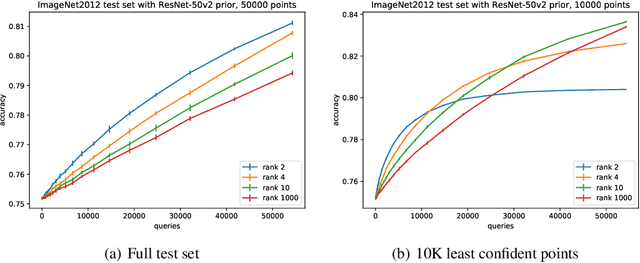
Abstract:Excessive reuse of holdout data can lead to overfitting. However, there is little concrete evidence of significant overfitting due to holdout reuse in popular multiclass benchmarks today. Known results show that, in the worst-case, revealing the accuracy of $k$ adaptively chosen classifiers on a data set of size $n$ allows to create a classifier with bias of $\Theta(\sqrt{k/n})$ for any binary prediction problem. We show a new upper bound of $\tilde O(\max\{\sqrt{k\log(n)/(mn)},k/n\})$ on the worst-case bias that any attack can achieve in a prediction problem with $m$ classes. Moreover, we present an efficient attack that achieve a bias of $\Omega(\sqrt{k/(m^2 n)})$ and improves on previous work for the binary setting ($m=2$). We also present an inefficient attack that achieves a bias of $\tilde\Omega(k/n)$. Complementing our theoretical work, we give new practical attacks to stress-test multiclass benchmarks by aiming to create as large a bias as possible with a given number of queries. Our experiments show that the additional uncertainty of prediction with a large number of classes indeed mitigates the effect of our best attacks. Our work extends developments in understanding overfitting due to adaptive data analysis to multiclass prediction problems. It also bears out the surprising fact that multiclass prediction problems are significantly more robust to overfitting when reusing a test (or holdout) dataset. This offers an explanation as to why popular multiclass prediction benchmarks, such as ImageNet, may enjoy a longer lifespan than what intuition from literature on binary classification suggests.
Measuring the Effects of Data Parallelism on Neural Network Training
Nov 21, 2018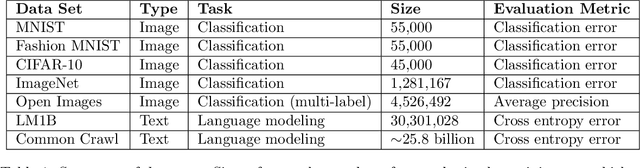
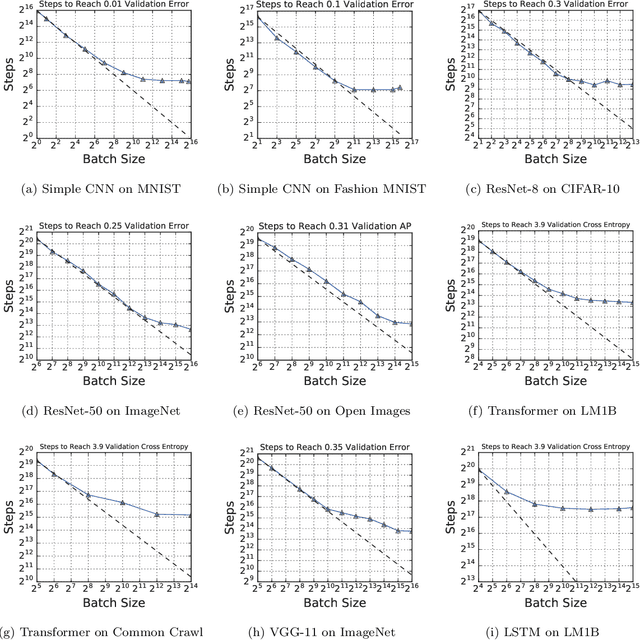
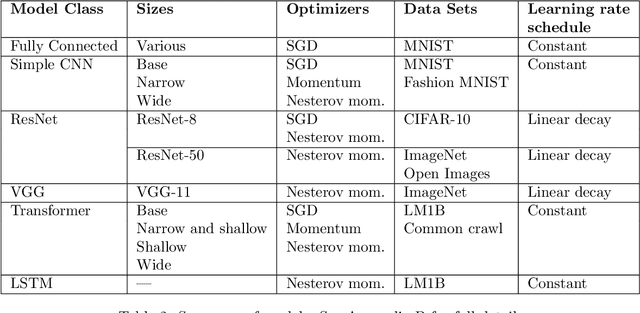
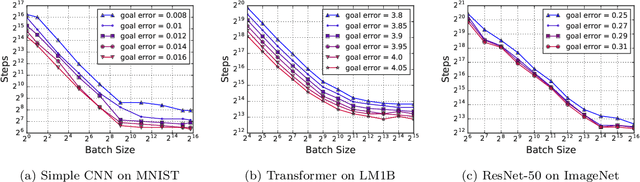
Abstract:Recent hardware developments have made unprecedented amounts of data parallelism available for accelerating neural network training. Among the simplest ways to harness next-generation accelerators is to increase the batch size in standard mini-batch neural network training algorithms. In this work, we aim to experimentally characterize the effects of increasing the batch size on training time, as measured in the number of steps necessary to reach a goal out-of-sample error. Eventually, increasing the batch size will no longer reduce the number of training steps required, but the exact relationship between the batch size and how many training steps are necessary is of critical importance to practitioners, researchers, and hardware designers alike. We study how this relationship varies with the training algorithm, model, and data set and find extremely large variation between workloads. Along the way, we reconcile disagreements in the literature on whether batch size affects model quality. Finally, we discuss the implications of our results for efforts to train neural networks much faster in the future.
Toward Deeper Understanding of Neural Networks: The Power of Initialization and a Dual View on Expressivity
May 19, 2017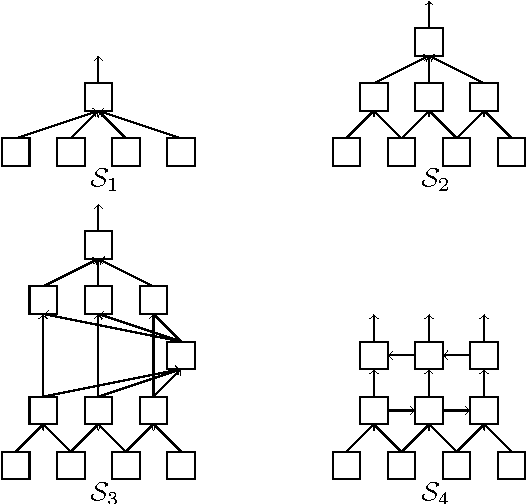

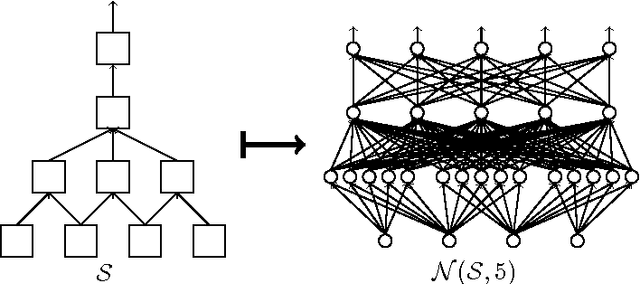
Abstract:We develop a general duality between neural networks and compositional kernels, striving towards a better understanding of deep learning. We show that initial representations generated by common random initializations are sufficiently rich to express all functions in the dual kernel space. Hence, though the training objective is hard to optimize in the worst case, the initial weights form a good starting point for optimization. Our dual view also reveals a pragmatic and aesthetic perspective of neural networks and underscores their expressive power.
Random Features for Compositional Kernels
Mar 22, 2017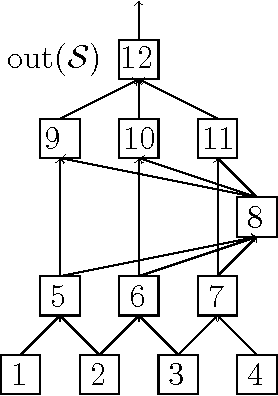
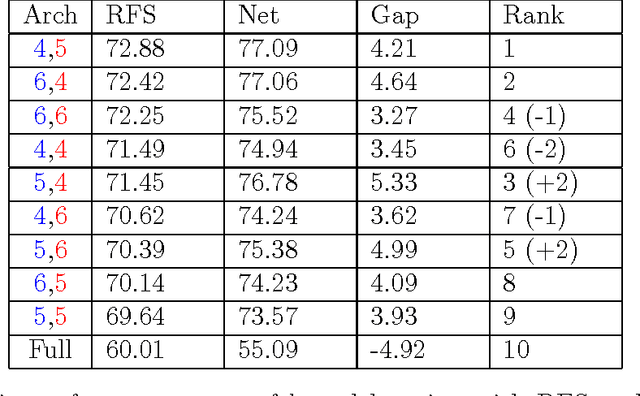
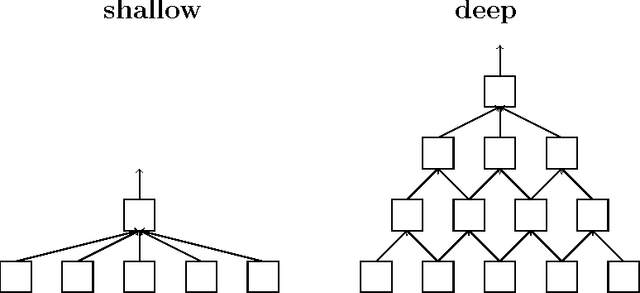
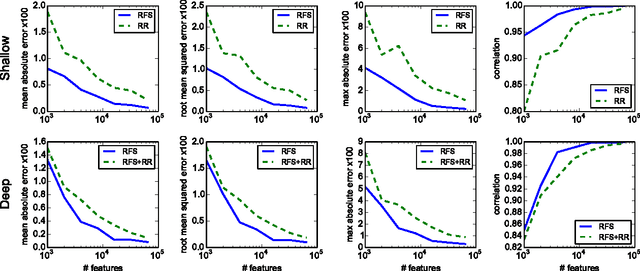
Abstract:We describe and analyze a simple random feature scheme (RFS) from prescribed compositional kernels. The compositional kernels we use are inspired by the structure of convolutional neural networks and kernels. The resulting scheme yields sparse and efficiently computable features. Each random feature can be represented as an algebraic expression over a small number of (random) paths in a composition tree. Thus, compositional random features can be stored compactly. The discrete nature of the generation process enables de-duplication of repeated features, further compacting the representation and increasing the diversity of the embeddings. Our approach complements and can be combined with previous random feature schemes.
Estimation from Indirect Supervision with Linear Moments
Aug 10, 2016
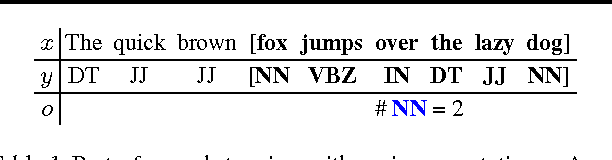
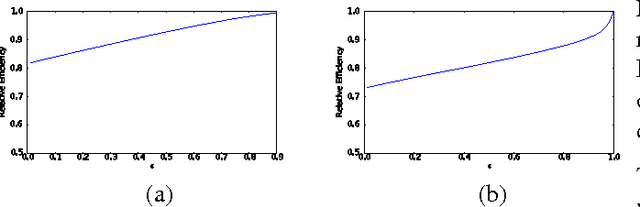
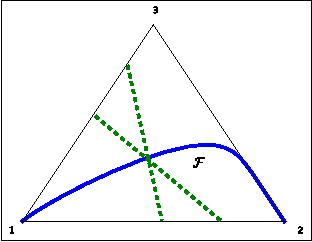
Abstract:In structured prediction problems where we have indirect supervision of the output, maximum marginal likelihood faces two computational obstacles: non-convexity of the objective and intractability of even a single gradient computation. In this paper, we bypass both obstacles for a class of what we call linear indirectly-supervised problems. Our approach is simple: we solve a linear system to estimate sufficient statistics of the model, which we then use to estimate parameters via convex optimization. We analyze the statistical properties of our approach and show empirically that it is effective in two settings: learning with local privacy constraints and learning from low-cost count-based annotations.
Principal Component Projection Without Principal Component Analysis
Feb 22, 2016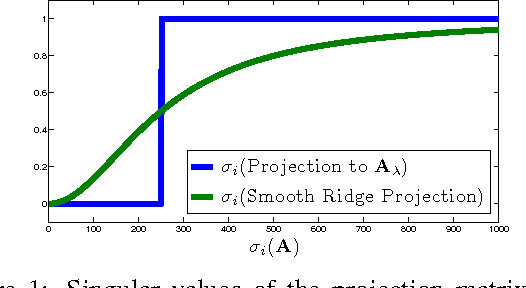
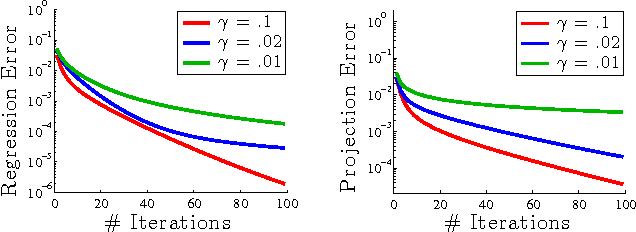
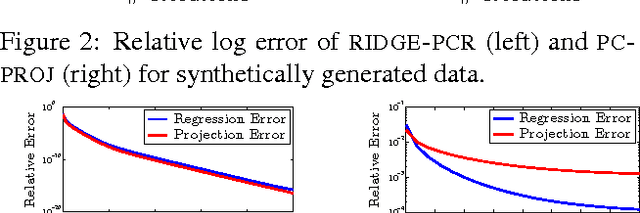
Abstract:We show how to efficiently project a vector onto the top principal components of a matrix, without explicitly computing these components. Specifically, we introduce an iterative algorithm that provably computes the projection using few calls to any black-box routine for ridge regression. By avoiding explicit principal component analysis (PCA), our algorithm is the first with no runtime dependence on the number of top principal components. We show that it can be used to give a fast iterative method for the popular principal component regression problem, giving the first major runtime improvement over the naive method of combining PCA with regression. To achieve our results, we first observe that ridge regression can be used to obtain a "smooth projection" onto the top principal components. We then sharpen this approximation to true projection using a low-degree polynomial approximation to the matrix step function. Step function approximation is a topic of long-term interest in scientific computing. We extend prior theory by constructing polynomials with simple iterative structure and rigorously analyzing their behavior under limited precision.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge