Scaling Exponents Across Parameterizations and Optimizers

Robust and effective scaling of models from small to large width typically requires the precise adjustment of many algorithmic and architectural details, such as parameterization and optimizer choices. In this work, we propose a new perspective on parameterization by investigating a key assumption in prior work about the alignment between parameters and data and derive new theoretical results under weaker assumptions and a broader set of optimizers. Our extensive empirical investigation includes tens of thousands of models trained with all combinations of three optimizers, four parameterizations, several alignment assumptions, more than a dozen learning rates, and fourteen model sizes up to 26.8B parameters. We find that the best learning rate scaling prescription would often have been excluded by the assumptions in prior work. Our results show that all parameterizations, not just maximal update parameterization (muP), can achieve hyperparameter transfer; moreover, our novel per-layer learning rate prescription for standard parameterization outperforms muP. Finally, we demonstrate that an overlooked aspect of parameterization, the epsilon parameter in Adam, must be scaled correctly to avoid gradient underflow and propose Adam-atan2, a new numerically stable, scale-invariant version of Adam that eliminates the epsilon hyperparameter entirely.

Training LLMs over Neurally Compressed Text

In this paper, we explore the idea of training large language models (LLMs) over highly compressed text. While standard subword tokenizers compress text by a small factor, neural text compressors can achieve much higher rates of compression. If it were possible to train LLMs directly over neurally compressed text, this would confer advantages in training and serving efficiency, as well as easier handling of long text spans. The main obstacle to this goal is that strong compression tends to produce opaque outputs that are not well-suited for learning. In particular, we find that text na\"ively compressed via Arithmetic Coding is not readily learnable by LLMs. To overcome this, we propose Equal-Info Windows, a novel compression technique whereby text is segmented into blocks that each compress to the same bit length. Using this method, we demonstrate effective learning over neurally compressed text that improves with scale, and outperforms byte-level baselines by a wide margin on perplexity and inference speed benchmarks. While our method delivers worse perplexity than subword tokenizers for models trained with the same parameter count, it has the benefit of shorter sequence lengths. Shorter sequence lengths require fewer autoregressive generation steps, and reduce latency. Finally, we provide extensive analysis of the properties that contribute to learnability, and offer concrete suggestions for how to further improve the performance of high-compression tokenizers.

The boundary of neural network trainability is fractal

Some fractals -- for instance those associated with the Mandelbrot and quadratic Julia sets -- are computed by iterating a function, and identifying the boundary between hyperparameters for which the resulting series diverges or remains bounded. Neural network training similarly involves iterating an update function (e.g. repeated steps of gradient descent), can result in convergent or divergent behavior, and can be extremely sensitive to small changes in hyperparameters. Motivated by these similarities, we experimentally examine the boundary between neural network hyperparameters that lead to stable and divergent training. We find that this boundary is fractal over more than ten decades of scale in all tested configurations.

Beyond Human Data: Scaling Self-Training for Problem-Solving with Language Models

Fine-tuning language models~(LMs) on human-generated data remains a prevalent practice. However, the performance of such models is often limited by the quantity and diversity of high-quality human data. In this paper, we explore whether we can go beyond human data on tasks where we have access to scalar feedback, for example, on math problems where one can verify correctness. To do so, we investigate a simple self-training method based on expectation-maximization, which we call ReST$^{EM}$, where we (1) generate samples from the model and filter them using binary feedback, (2) fine-tune the model on these samples, and (3) repeat this process a few times. Testing on advanced MATH reasoning and APPS coding benchmarks using PaLM-2 models, we find that ReST$^{EM}$ scales favorably with model size and significantly surpasses fine-tuning only on human data. Overall, our findings suggest self-training with feedback can substantially reduce dependence on human-generated data.

Frontier Language Models are not Robust to Adversarial Arithmetic, or "What do I need to say so you agree 2+2=5?

We introduce and study the problem of adversarial arithmetic, which provides a simple yet challenging testbed for language model alignment. This problem is comprised of arithmetic questions posed in natural language, with an arbitrary adversarial string inserted before the question is complete. Even in the simple setting of 1-digit addition problems, it is easy to find adversarial prompts that make all tested models (including PaLM2, GPT4, Claude2) misbehave, and even to steer models to a particular wrong answer. We additionally provide a simple algorithm for finding successful attacks by querying those same models, which we name "prompt inversion rejection sampling" (PIRS). We finally show that models can be partially hardened against these attacks via reinforcement learning and via agentic constitutional loops. However, we were not able to make a language model fully robust against adversarial arithmetic attacks.

Noise-Reuse in Online Evolution Strategies

Online evolution strategies have become an attractive alternative to automatic differentiation (AD) due to their ability to handle chaotic and black-box loss functions, while also allowing more frequent gradient updates than vanilla Evolution Strategies (ES). In this work, we propose a general class of unbiased online evolution strategies. We analytically and empirically characterize the variance of this class of gradient estimators and identify the one with the least variance, which we term Noise-Reuse Evolution Strategies (NRES). Experimentally, we show that NRES results in faster convergence than existing AD and ES methods in terms of wall-clock speed and total number of unroll steps across a variety of applications, including learning dynamical systems, meta-training learned optimizers, and reinforcement learning.

Reduce, Reuse, Recycle: Compositional Generation with Energy-Based Diffusion Models and MCMC

Since their introduction, diffusion models have quickly become the prevailing approach to generative modeling in many domains. They can be interpreted as learning the gradients of a time-varying sequence of log-probability density functions. This interpretation has motivated classifier-based and classifier-free guidance as methods for post-hoc control of diffusion models. In this work, we build upon these ideas using the score-based interpretation of diffusion models, and explore alternative ways to condition, modify, and reuse diffusion models for tasks involving compositional generation and guidance. In particular, we investigate why certain types of composition fail using current techniques and present a number of solutions. We conclude that the sampler (not the model) is responsible for this failure and propose new samplers, inspired by MCMC, which enable successful compositional generation. Further, we propose an energy-based parameterization of diffusion models which enables the use of new compositional operators and more sophisticated, Metropolis-corrected samplers. Intriguingly we find these samplers lead to notable improvements in compositional generation across a wide set of problems such as classifier-guided ImageNet modeling and compositional text-to-image generation.

General-Purpose In-Context Learning by Meta-Learning Transformers

Modern machine learning requires system designers to specify aspects of the learning pipeline, such as losses, architectures, and optimizers. Meta-learning, or learning-to-learn, instead aims to learn those aspects, and promises to unlock greater capabilities with less manual effort. One particularly ambitious goal of meta-learning is to train general-purpose in-context learning algorithms from scratch, using only black-box models with minimal inductive bias. Such a model takes in training data, and produces test-set predictions across a wide range of problems, without any explicit definition of an inference model, training loss, or optimization algorithm. In this paper we show that Transformers and other black-box models can be meta-trained to act as general-purpose in-context learners. We characterize phase transitions between algorithms that generalize, algorithms that memorize, and algorithms that fail to meta-train at all, induced by changes in model size, number of tasks, and meta-optimization. We further show that the capabilities of meta-trained algorithms are bottlenecked by the accessible state size (memory) determining the next prediction, unlike standard models which are thought to be bottlenecked by parameter count. Finally, we propose practical interventions such as biasing the training distribution that improve the meta-training and meta-generalization of general-purpose learning algorithms.

VeLO: Training Versatile Learned Optimizers by Scaling Up

While deep learning models have replaced hand-designed features across many domains, these models are still trained with hand-designed optimizers. In this work, we leverage the same scaling approach behind the success of deep learning to learn versatile optimizers. We train an optimizer for deep learning which is itself a small neural network that ingests gradients and outputs parameter updates. Meta-trained with approximately four thousand TPU-months of compute on a wide variety of optimization tasks, our optimizer not only exhibits compelling performance, but optimizes in interesting and unexpected ways. It requires no hyperparameter tuning, instead automatically adapting to the specifics of the problem being optimized. We open source our learned optimizer, meta-training code, the associated train and test data, and an extensive optimizer benchmark suite with baselines at velo-code.github.io.

A Closer Look at Learned Optimization: Stability, Robustness, and Inductive Biases

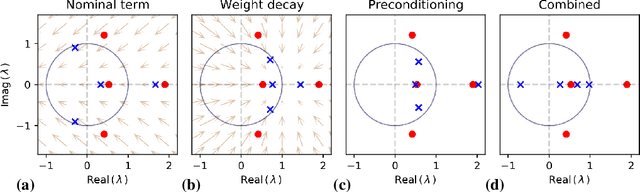
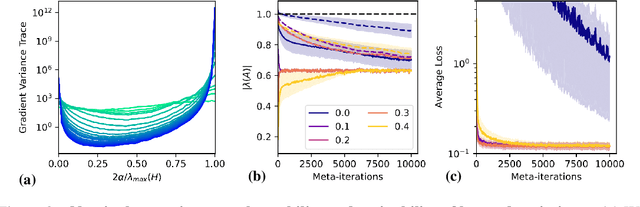
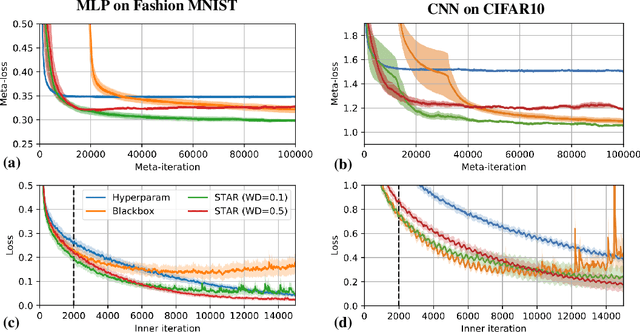
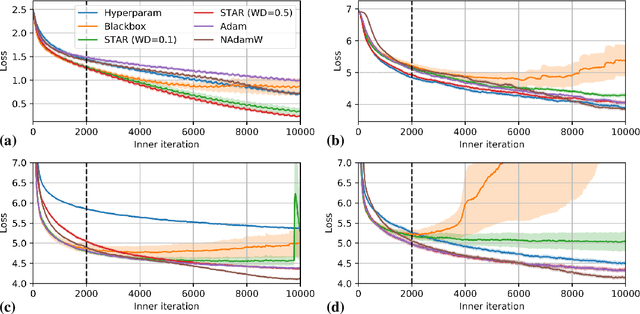
Learned optimizers -- neural networks that are trained to act as optimizers -- have the potential to dramatically accelerate training of machine learning models. However, even when meta-trained across thousands of tasks at huge computational expense, blackbox learned optimizers often struggle with stability and generalization when applied to tasks unlike those in their meta-training set. In this paper, we use tools from dynamical systems to investigate the inductive biases and stability properties of optimization algorithms, and apply the resulting insights to designing inductive biases for blackbox optimizers. Our investigation begins with a noisy quadratic model, where we characterize conditions in which optimization is stable, in terms of eigenvalues of the training dynamics. We then introduce simple modifications to a learned optimizer's architecture and meta-training procedure which lead to improved stability, and improve the optimizer's inductive bias. We apply the resulting learned optimizer to a variety of neural network training tasks, where it outperforms the current state of the art learned optimizer -- at matched optimizer computational overhead -- with regard to optimization performance and meta-training speed, and is capable of generalization to tasks far different from those it was meta-trained on.