Alexey Radul
Decomposing reverse-mode automatic differentiation
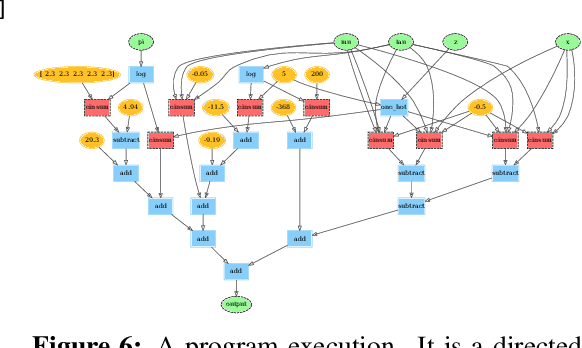
May 20, 2021Abstract:We decompose reverse-mode automatic differentiation into (forward-mode) linearization followed by transposition. Doing so isolates the essential difference between forward- and reverse-mode AD, and simplifies their joint implementation. In particular, once forward-mode AD rules are defined for every primitive operation in a source language, only linear primitives require an additional transposition rule in order to arrive at a complete reverse-mode AD implementation. This is how reverse-mode AD is written in JAX and Dex.
Automatically Batching Control-Intensive Programs for Modern Accelerators
Oct 23, 2019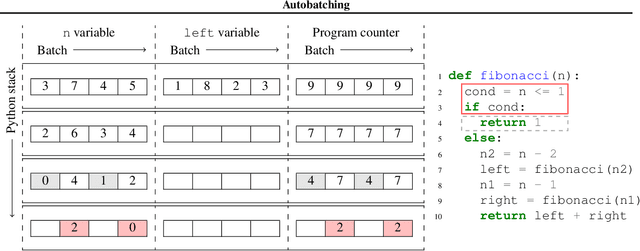

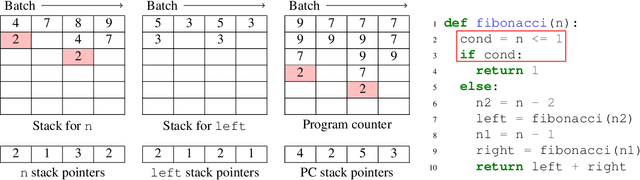

Abstract:We present a general approach to batching arbitrary computations for accelerators such as GPUs. We show orders-of-magnitude speedups using our method on the No U-Turn Sampler (NUTS), a workhorse algorithm in Bayesian statistics. The central challenge of batching NUTS and other Markov chain Monte Carlo algorithms is data-dependent control flow and recursion. We overcome this by mechanically transforming a single-example implementation into a form that explicitly tracks the current program point for each batch member, and only steps forward those in the same place. We present two different batching algorithms: a simpler, previously published one that inherits recursion from the host Python, and a more complex, novel one that implemenents recursion directly and can batch across it. We implement these batching methods as a general program transformation on Python source. Both the batching system and the NUTS implementation presented here are available as part of the popular TensorFlow Probability software package.
Simple, Distributed, and Accelerated Probabilistic Programming
Nov 29, 2018
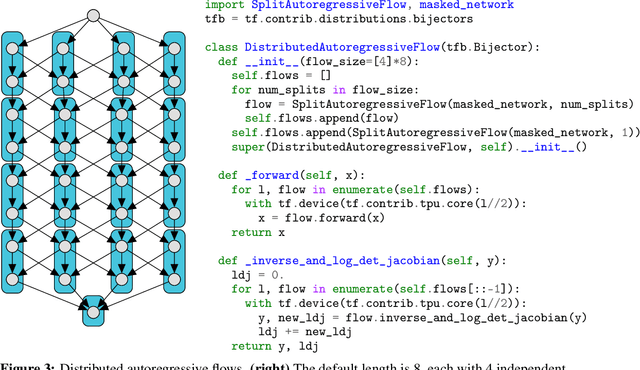
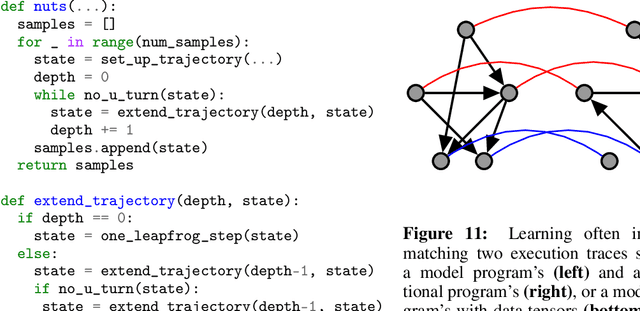
Abstract:We describe a simple, low-level approach for embedding probabilistic programming in a deep learning ecosystem. In particular, we distill probabilistic programming down to a single abstraction---the random variable. Our lightweight implementation in TensorFlow enables numerous applications: a model-parallel variational auto-encoder (VAE) with 2nd-generation tensor processing units (TPUv2s); a data-parallel autoregressive model (Image Transformer) with TPUv2s; and multi-GPU No-U-Turn Sampler (NUTS). For both a state-of-the-art VAE on 64x64 ImageNet and Image Transformer on 256x256 CelebA-HQ, our approach achieves an optimal linear speedup from 1 to 256 TPUv2 chips. With NUTS, we see a 100x speedup on GPUs over Stan and 37x over PyMC3.
Time Series Structure Discovery via Probabilistic Program Synthesis
May 22, 2017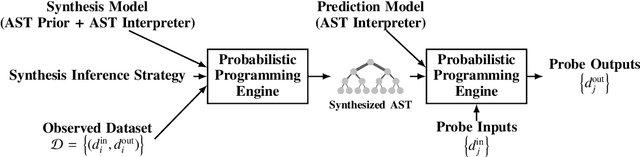


Abstract:There is a widespread need for techniques that can discover structure from time series data. Recently introduced techniques such as Automatic Bayesian Covariance Discovery (ABCD) provide a way to find structure within a single time series by searching through a space of covariance kernels that is generated using a simple grammar. While ABCD can identify a broad class of temporal patterns, it is difficult to extend and can be brittle in practice. This paper shows how to extend ABCD by formulating it in terms of probabilistic program synthesis. The key technical ideas are to (i) represent models using abstract syntax trees for a domain-specific probabilistic language, and (ii) represent the time series model prior, likelihood, and search strategy using probabilistic programs in a sufficiently expressive language. The final probabilistic program is written in under 70 lines of probabilistic code in Venture. The paper demonstrates an application to time series clustering that involves a non-parametric extension to ABCD, experiments for interpolation and extrapolation on real-world econometric data, and improvements in accuracy over both non-parametric and standard regression baselines.
Probabilistic programs for inferring the goals of autonomous agents
Apr 18, 2017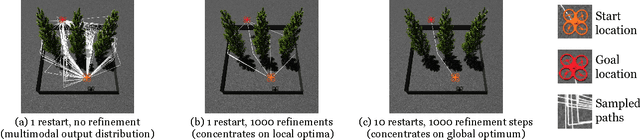
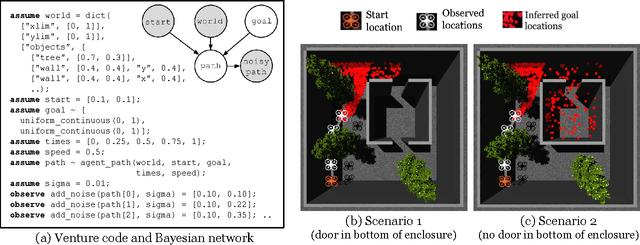
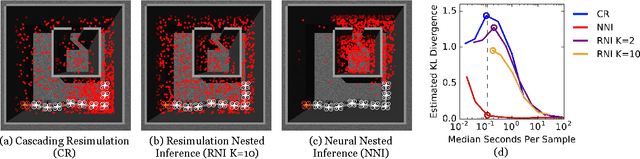
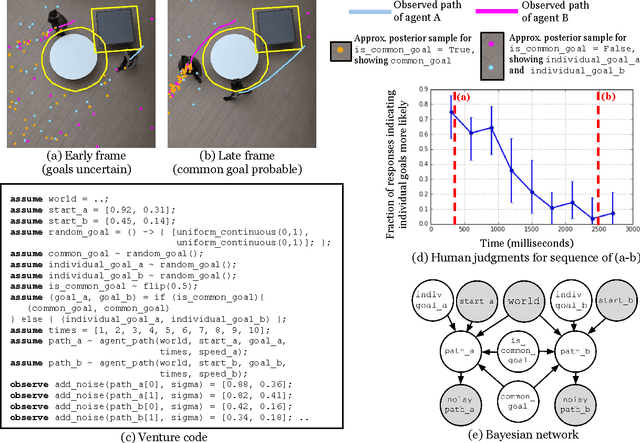
Abstract:Intelligent systems sometimes need to infer the probable goals of people, cars, and robots, based on partial observations of their motion. This paper introduces a class of probabilistic programs for formulating and solving these problems. The formulation uses randomized path planning algorithms as the basis for probabilistic models of the process by which autonomous agents plan to achieve their goals. Because these path planning algorithms do not have tractable likelihood functions, new inference algorithms are needed. This paper proposes two Monte Carlo techniques for these "likelihood-free" models, one of which can use likelihood estimates from neural networks to accelerate inference. The paper demonstrates efficacy on three simple examples, each using under 50 lines of probabilistic code.
Probabilistic Programming with Gaussian Process Memoization
Jan 05, 2016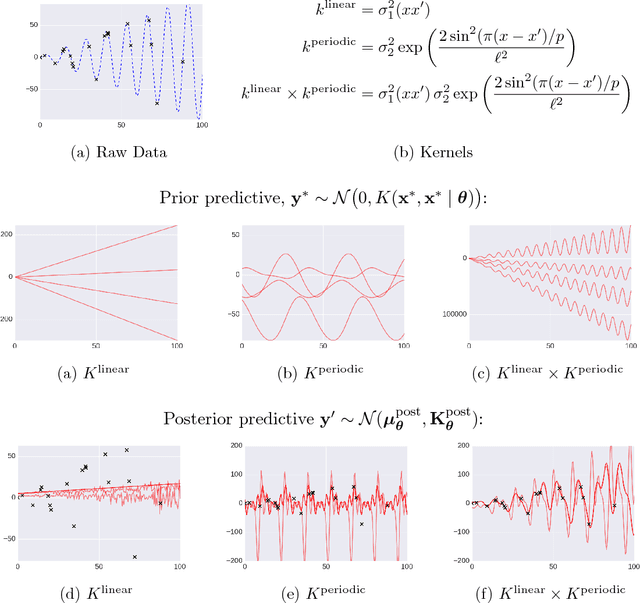
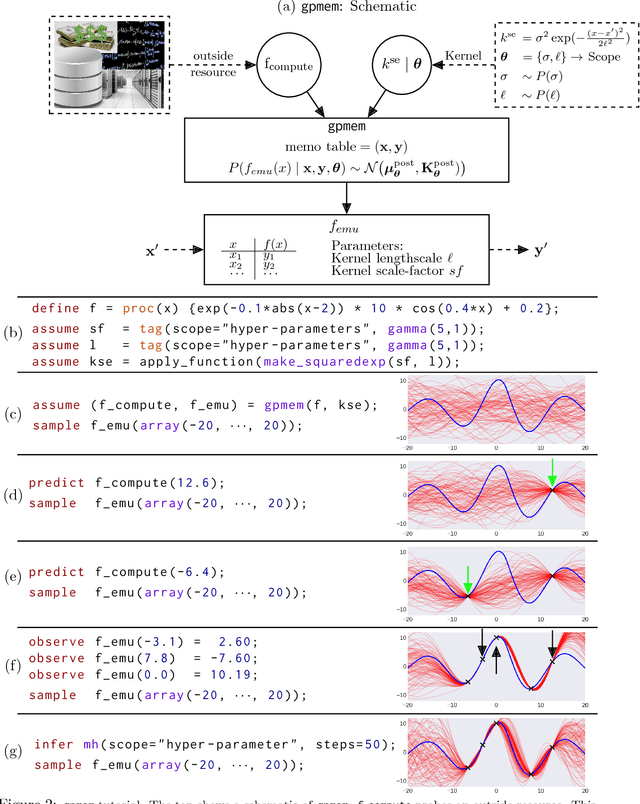
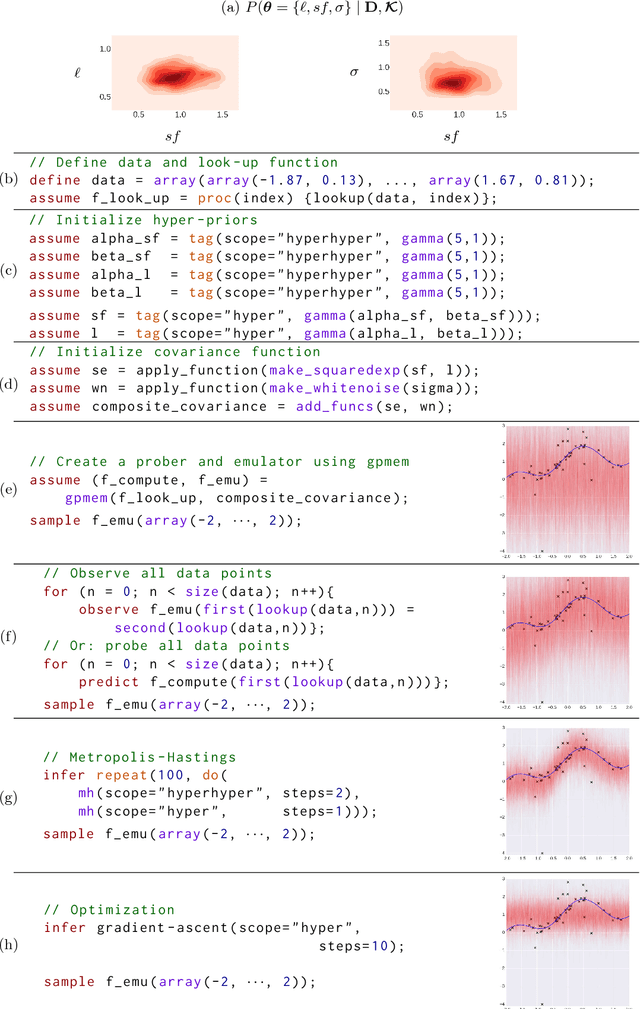
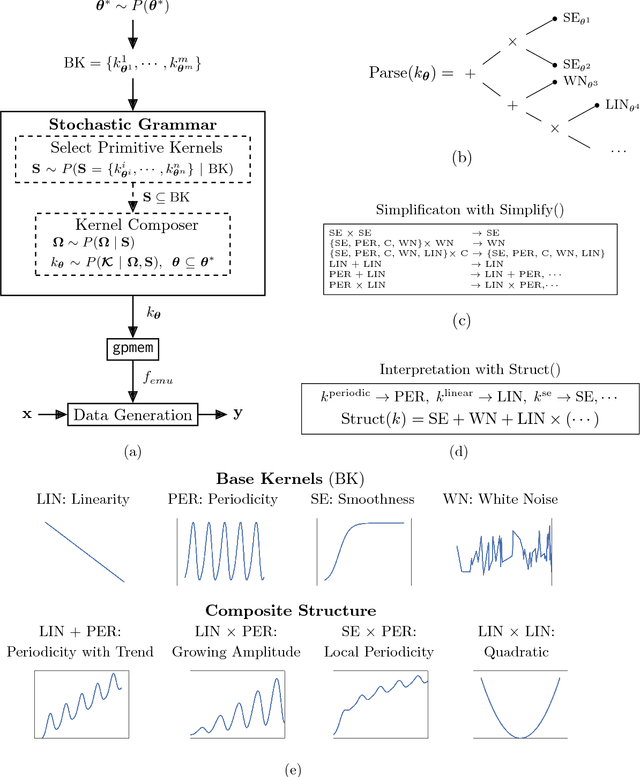
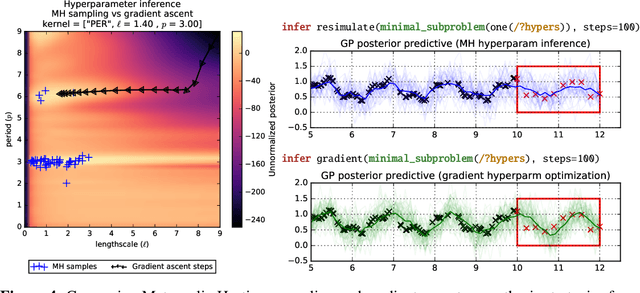
Abstract:Gaussian Processes (GPs) are widely used tools in statistics, machine learning, robotics, computer vision, and scientific computation. However, despite their popularity, they can be difficult to apply; all but the simplest classification or regression applications require specification and inference over complex covariance functions that do not admit simple analytical posteriors. This paper shows how to embed Gaussian processes in any higher-order probabilistic programming language, using an idiom based on memoization, and demonstrates its utility by implementing and extending classic and state-of-the-art GP applications. The interface to Gaussian processes, called gpmem, takes an arbitrary real-valued computational process as input and returns a statistical emulator that automatically improve as the original process is invoked and its input-output behavior is recorded. The flexibility of gpmem is illustrated via three applications: (i) robust GP regression with hierarchical hyper-parameter learning, (ii) discovering symbolic expressions from time-series data by fully Bayesian structure learning over kernels generated by a stochastic grammar, and (iii) a bandit formulation of Bayesian optimization with automatic inference and action selection. All applications share a single 50-line Python library and require fewer than 20 lines of probabilistic code each.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge