John Duchi
Resampling methods for Private Statistical Inference
Feb 11, 2024Abstract:We consider the task of constructing confidence intervals with differential privacy. We propose two private variants of the non-parametric bootstrap, which privately compute the median of the results of multiple ``little'' bootstraps run on partitions of the data and give asymptotic bounds on the coverage error of the resulting confidence intervals. For a fixed differential privacy parameter $\epsilon$, our methods enjoy the same error rates as that of the non-private bootstrap to within logarithmic factors in the sample size $n$. We empirically validate the performance of our methods for mean estimation, median estimation, and logistic regression with both real and synthetic data. Our methods achieve similar coverage accuracy to existing methods (and non-private baselines) while providing notably shorter ($\gtrsim 10$ times) confidence intervals than previous approaches.
Collaboratively Learning Linear Models with Structured Missing Data
Jul 22, 2023



Abstract:We study the problem of collaboratively learning least squares estimates for $m$ agents. Each agent observes a different subset of the features$\unicode{x2013}$e.g., containing data collected from sensors of varying resolution. Our goal is to determine how to coordinate the agents in order to produce the best estimator for each agent. We propose a distributed, semi-supervised algorithm Collab, consisting of three steps: local training, aggregation, and distribution. Our procedure does not require communicating the labeled data, making it communication efficient and useful in settings where the labeled data is inaccessible. Despite this handicap, our procedure is nearly asymptotically local minimax optimal$\unicode{x2013}$even among estimators allowed to communicate the labeled data such as imputation methods. We test our method on real and synthetic data.
Differentially Private Heavy Hitter Detection using Federated Analytics
Jul 21, 2023



Abstract:In this work, we study practical heuristics to improve the performance of prefix-tree based algorithms for differentially private heavy hitter detection. Our model assumes each user has multiple data points and the goal is to learn as many of the most frequent data points as possible across all users' data with aggregate and local differential privacy. We propose an adaptive hyperparameter tuning algorithm that improves the performance of the algorithm while satisfying computational, communication and privacy constraints. We explore the impact of different data-selection schemes as well as the impact of introducing deny lists during multiple runs of the algorithm. We test these improvements using extensive experimentation on the Reddit dataset~\cite{caldas2018leaf} on the task of learning the most frequent words.
A Fast Algorithm for Adaptive Private Mean Estimation
Jan 17, 2023Abstract:We design an $(\varepsilon, \delta)$-differentially private algorithm to estimate the mean of a $d$-variate distribution, with unknown covariance $\Sigma$, that is adaptive to $\Sigma$. To within polylogarithmic factors, the estimator achieves optimal rates of convergence with respect to the induced Mahalanobis norm $||\cdot||_\Sigma$, takes time $\tilde{O}(n d^2)$ to compute, has near linear sample complexity for sub-Gaussian distributions, allows $\Sigma$ to be degenerate or low rank, and adaptively extends beyond sub-Gaussianity. Prior to this work, other methods required exponential computation time or the superlinear scaling $n = \Omega(d^{3/2})$ to achieve non-trivial error with respect to the norm $||\cdot||_\Sigma$.
Private optimization in the interpolation regime: faster rates and hardness results
Oct 31, 2022Abstract:In non-private stochastic convex optimization, stochastic gradient methods converge much faster on interpolation problems -- problems where there exists a solution that simultaneously minimizes all of the sample losses -- than on non-interpolating ones; we show that generally similar improvements are impossible in the private setting. However, when the functions exhibit quadratic growth around the optimum, we show (near) exponential improvements in the private sample complexity. In particular, we propose an adaptive algorithm that improves the sample complexity to achieve expected error $\alpha$ from $\frac{d}{\varepsilon \sqrt{\alpha}}$ to $\frac{1}{\alpha^\rho} + \frac{d}{\varepsilon} \log\left(\frac{1}{\alpha}\right)$ for any fixed $\rho >0$, while retaining the standard minimax-optimal sample complexity for non-interpolation problems. We prove a lower bound that shows the dimension-dependent term is tight. Furthermore, we provide a superefficiency result which demonstrates the necessity of the polynomial term for adaptive algorithms: any algorithm that has a polylogarithmic sample complexity for interpolation problems cannot achieve the minimax-optimal rates for the family of non-interpolation problems.
Subspace Recovery from Heterogeneous Data with Non-isotropic Noise
Oct 24, 2022Abstract:Recovering linear subspaces from data is a fundamental and important task in statistics and machine learning. Motivated by heterogeneity in Federated Learning settings, we study a basic formulation of this problem: the principal component analysis (PCA), with a focus on dealing with irregular noise. Our data come from $n$ users with user $i$ contributing data samples from a $d$-dimensional distribution with mean $\mu_i$. Our goal is to recover the linear subspace shared by $\mu_1,\ldots,\mu_n$ using the data points from all users, where every data point from user $i$ is formed by adding an independent mean-zero noise vector to $\mu_i$. If we only have one data point from every user, subspace recovery is information-theoretically impossible when the covariance matrices of the noise vectors can be non-spherical, necessitating additional restrictive assumptions in previous work. We avoid these assumptions by leveraging at least two data points from each user, which allows us to design an efficiently-computable estimator under non-spherical and user-dependent noise. We prove an upper bound for the estimation error of our estimator in general scenarios where the number of data points and amount of noise can vary across users, and prove an information-theoretic error lower bound that not only matches the upper bound up to a constant factor, but also holds even for spherical Gaussian noise. This implies that our estimator does not introduce additional estimation error (up to a constant factor) due to irregularity in the noise. We show additional results for a linear regression problem in a similar setup.
How many labelers do you have? A closer look at gold-standard labels
Jun 24, 2022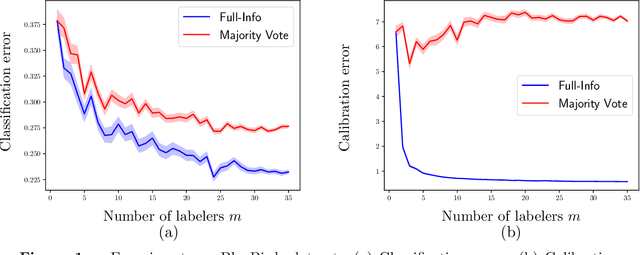
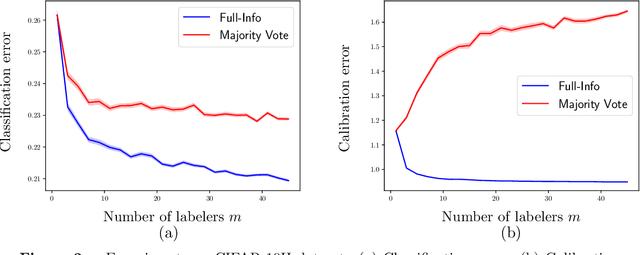
Abstract:The construction of most supervised learning datasets revolves around collecting multiple labels for each instance, then aggregating the labels to form a type of ``gold-standard.''. We question the wisdom of this pipeline by developing a (stylized) theoretical model of this process and analyzing its statistical consequences, showing how access to non-aggregated label information can make training well-calibrated models easier or -- in some cases -- even feasible, whereas it is impossible with only gold-standard labels. The entire story, however, is subtle, and the contrasts between aggregated and fuller label information depend on the particulars of the problem, where estimators that use aggregated information exhibit robust but slower rates of convergence, while estimators that can effectively leverage all labels converge more quickly if they have fidelity to (or can learn) the true labeling process. The theory we develop in the stylized model makes several predictions for real-world datasets, including when non-aggregate labels should improve learning performance, which we test to corroborate the validity of our predictions.
Query-Adaptive Predictive Inference with Partial Labels
Jun 15, 2022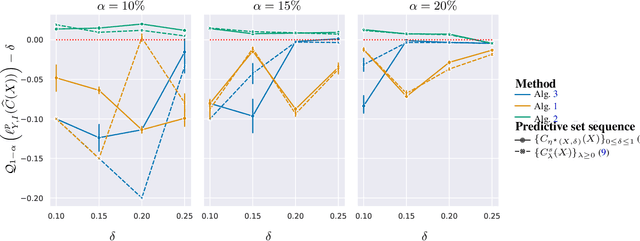
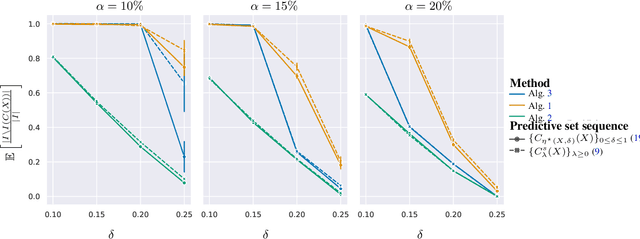
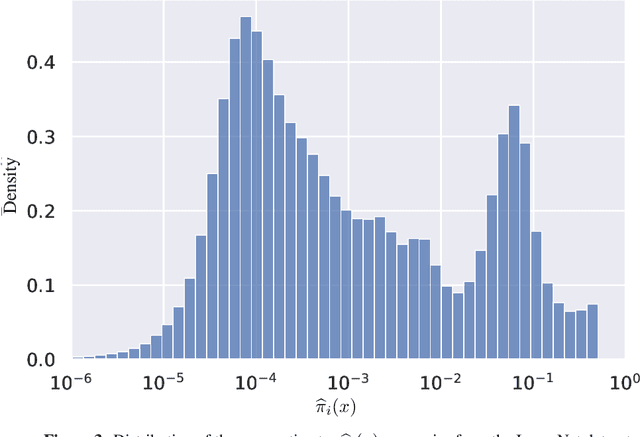
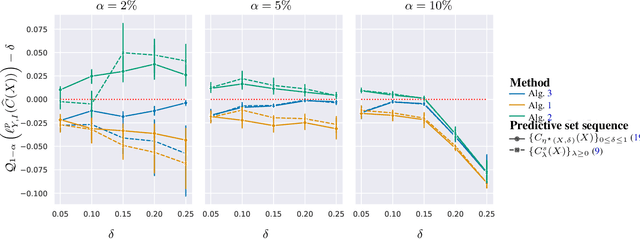
Abstract:The cost and scarcity of fully supervised labels in statistical machine learning encourage using partially labeled data for model validation as a cheaper and more accessible alternative. Effectively collecting and leveraging weakly supervised data for large-space structured prediction tasks thus becomes an important part of an end-to-end learning system. We propose a new computationally-friendly methodology to construct predictive sets using only partially labeled data on top of black-box predictive models. To do so, we introduce "probe" functions as a way to describe weakly supervised instances and define a false discovery proportion-type loss, both of which seamlessly adapt to partial supervision and structured prediction -- ranking, matching, segmentation, multilabel or multiclass classification. Our experiments highlight the validity of our predictive set construction as well as the attractiveness of a more flexible user-dependent loss framework.
Memorize to Generalize: on the Necessity of Interpolation in High Dimensional Linear Regression
Feb 20, 2022Abstract:We examine the necessity of interpolation in overparameterized models, that is, when achieving optimal predictive risk in machine learning problems requires (nearly) interpolating the training data. In particular, we consider simple overparameterized linear regression $y = X \theta + w$ with random design $X \in \mathbb{R}^{n \times d}$ under the proportional asymptotics $d/n \to \gamma \in (1, \infty)$. We precisely characterize how prediction (test) error necessarily scales with training error in this setting. An implication of this characterization is that as the label noise variance $\sigma^2 \to 0$, any estimator that incurs at least $\mathsf{c}\sigma^4$ training error for some constant $\mathsf{c}$ is necessarily suboptimal and will suffer growth in excess prediction error at least linear in the training error. Thus, optimal performance requires fitting training data to substantially higher accuracy than the inherent noise floor of the problem.
Predictive Inference with Weak Supervision
Feb 09, 2022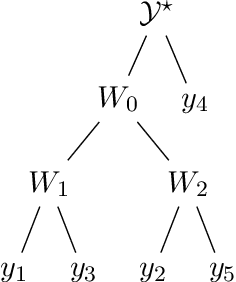
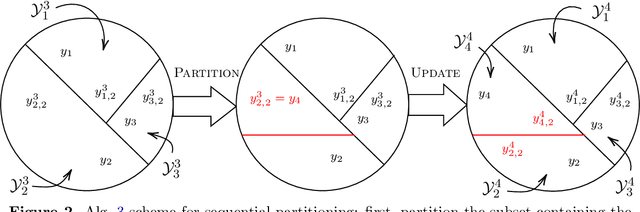
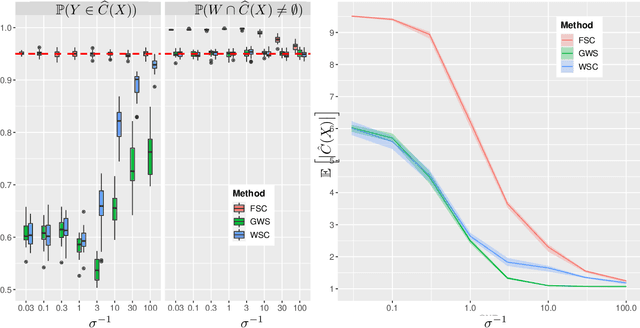
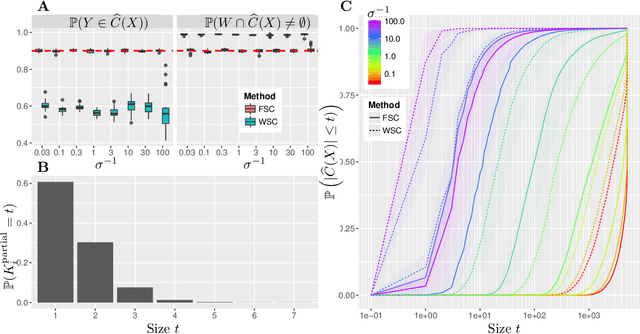
Abstract:The expense of acquiring labels in large-scale statistical machine learning makes partially and weakly-labeled data attractive, though it is not always apparent how to leverage such data for model fitting or validation. We present a methodology to bridge the gap between partial supervision and validation, developing a conformal prediction framework to provide valid predictive confidence sets -- sets that cover a true label with a prescribed probability, independent of the underlying distribution -- using weakly labeled data. To do so, we introduce a (necessary) new notion of coverage and predictive validity, then develop several application scenarios, providing efficient algorithms for classification and several large-scale structured prediction problems. We corroborate the hypothesis that the new coverage definition allows for tighter and more informative (but valid) confidence sets through several experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge