PartIR: Composing SPMD Partitioning Strategies for Machine Learning

Training of modern large neural networks (NN) requires a combination of parallelization strategies encompassing data, model, or optimizer sharding. When strategies increase in complexity, it becomes necessary for partitioning tools to be 1) expressive, allowing the composition of simpler strategies, and 2) predictable to estimate performance analytically. We present PartIR, our design for a NN partitioning system. PartIR is focused on an incremental approach to rewriting and is hardware-and-runtime agnostic. We present a simple but powerful API for composing sharding strategies and a simulator to validate them. The process is driven by high-level programmer-issued partitioning tactics, which can be both manual and automatic. Importantly, the tactics are specified separately from the model code, making them easy to change. We evaluate PartIR on several different models to demonstrate its predictability, expressibility, and ability to reach peak performance..

Decomposing reverse-mode automatic differentiation

We decompose reverse-mode automatic differentiation into (forward-mode) linearization followed by transposition. Doing so isolates the essential difference between forward- and reverse-mode AD, and simplifies their joint implementation. In particular, once forward-mode AD rules are defined for every primitive operation in a source language, only linear primitives require an additional transposition rule in order to arrive at a complete reverse-mode AD implementation. This is how reverse-mode AD is written in JAX and Dex.

Automatically Batching Control-Intensive Programs for Modern Accelerators

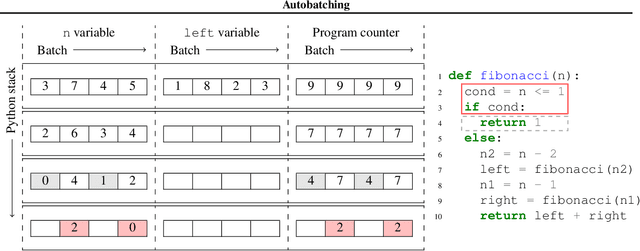
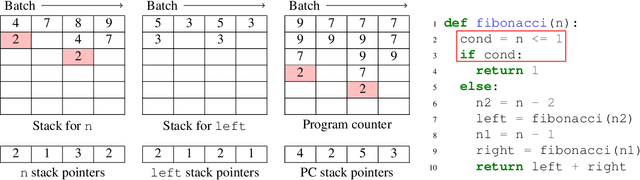
We present a general approach to batching arbitrary computations for accelerators such as GPUs. We show orders-of-magnitude speedups using our method on the No U-Turn Sampler (NUTS), a workhorse algorithm in Bayesian statistics. The central challenge of batching NUTS and other Markov chain Monte Carlo algorithms is data-dependent control flow and recursion. We overcome this by mechanically transforming a single-example implementation into a form that explicitly tracks the current program point for each batch member, and only steps forward those in the same place. We present two different batching algorithms: a simpler, previously published one that inherits recursion from the host Python, and a more complex, novel one that implemenents recursion directly and can batch across it. We implement these batching methods as a general program transformation on Python source. Both the batching system and the NUTS implementation presented here are available as part of the popular TensorFlow Probability software package.

Convolutional Networks on Graphs for Learning Molecular Fingerprints

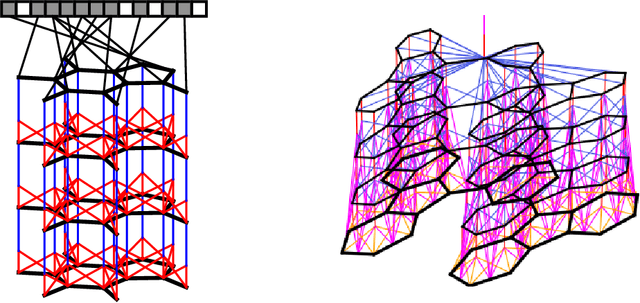
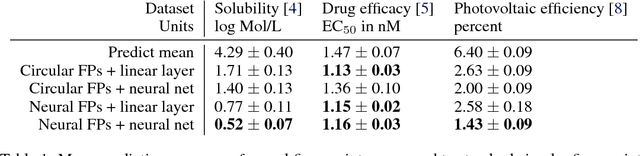
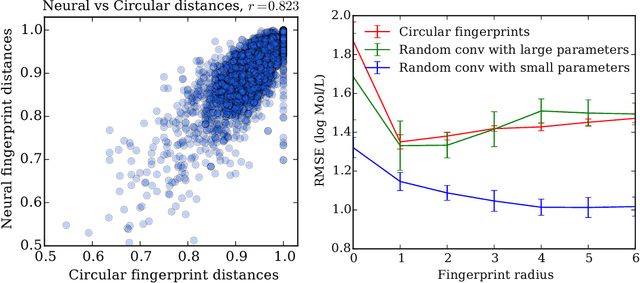
We introduce a convolutional neural network that operates directly on graphs. These networks allow end-to-end learning of prediction pipelines whose inputs are graphs of arbitrary size and shape. The architecture we present generalizes standard molecular feature extraction methods based on circular fingerprints. We show that these data-driven features are more interpretable, and have better predictive performance on a variety of tasks.

Early Stopping is Nonparametric Variational Inference

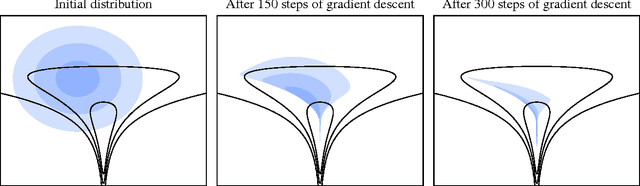
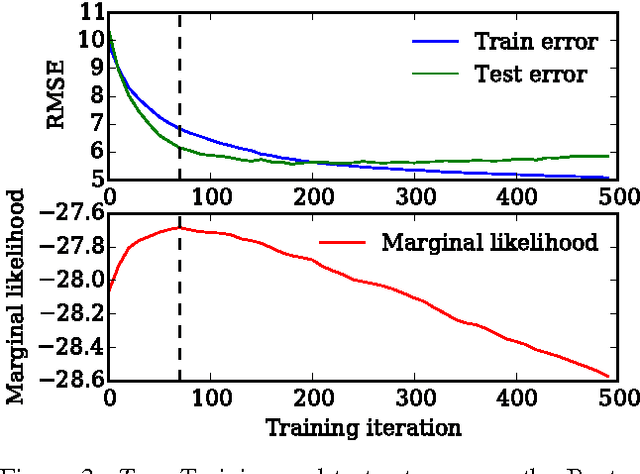
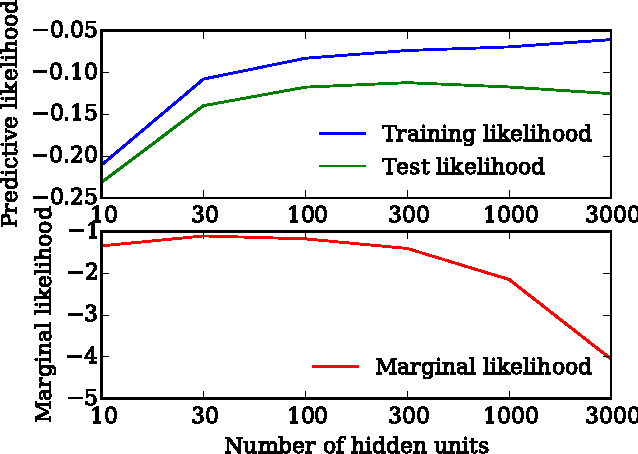
We show that unconverged stochastic gradient descent can be interpreted as a procedure that samples from a nonparametric variational approximate posterior distribution. This distribution is implicitly defined as the transformation of an initial distribution by a sequence of optimization updates. By tracking the change in entropy over this sequence of transformations during optimization, we form a scalable, unbiased estimate of the variational lower bound on the log marginal likelihood. We can use this bound to optimize hyperparameters instead of using cross-validation. This Bayesian interpretation of SGD suggests improved, overfitting-resistant optimization procedures, and gives a theoretical foundation for popular tricks such as early stopping and ensembling. We investigate the properties of this marginal likelihood estimator on neural network models.

Gradient-based Hyperparameter Optimization through Reversible Learning

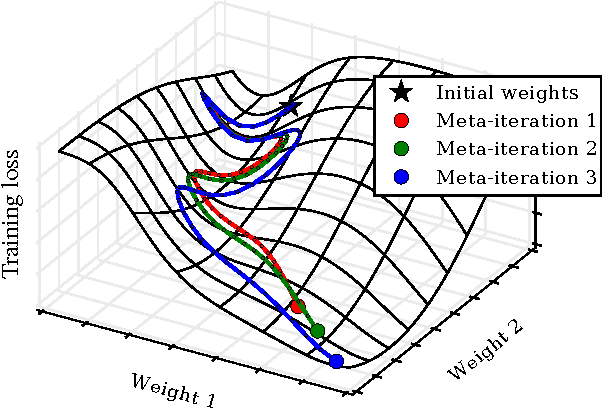
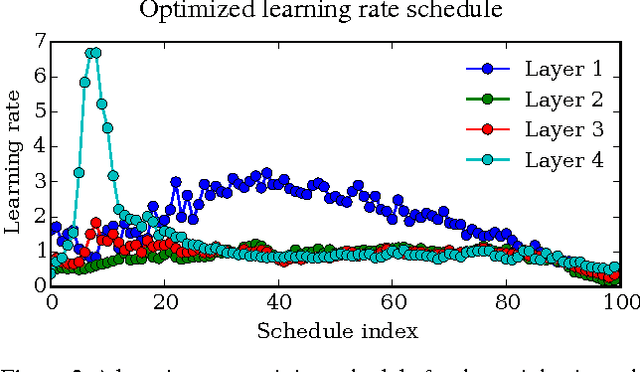
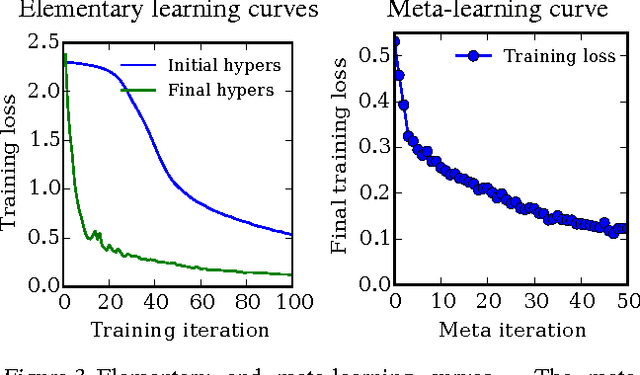
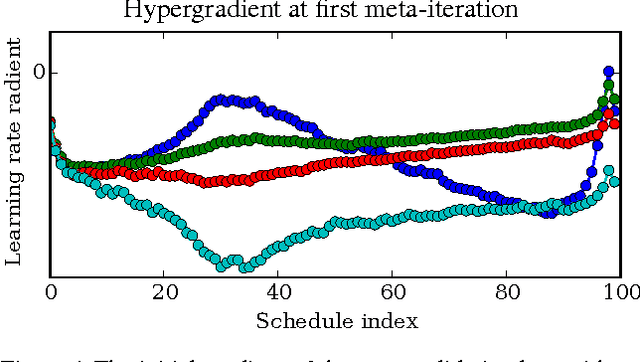
Tuning hyperparameters of learning algorithms is hard because gradients are usually unavailable. We compute exact gradients of cross-validation performance with respect to all hyperparameters by chaining derivatives backwards through the entire training procedure. These gradients allow us to optimize thousands of hyperparameters, including step-size and momentum schedules, weight initialization distributions, richly parameterized regularization schemes, and neural network architectures. We compute hyperparameter gradients by exactly reversing the dynamics of stochastic gradient descent with momentum.

Firefly Monte Carlo: Exact MCMC with Subsets of Data

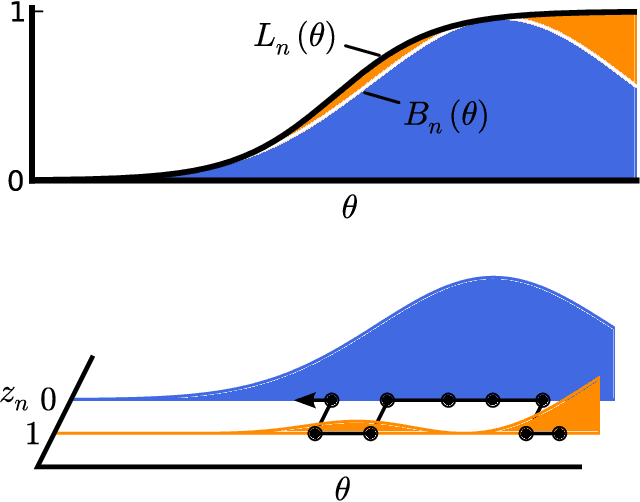
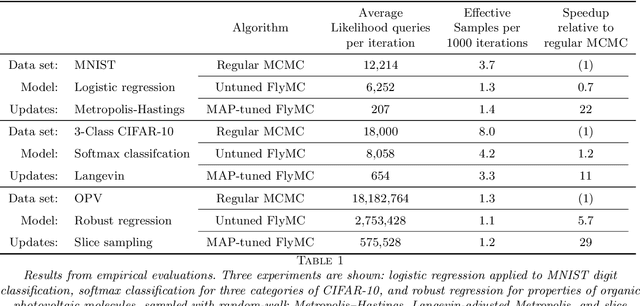
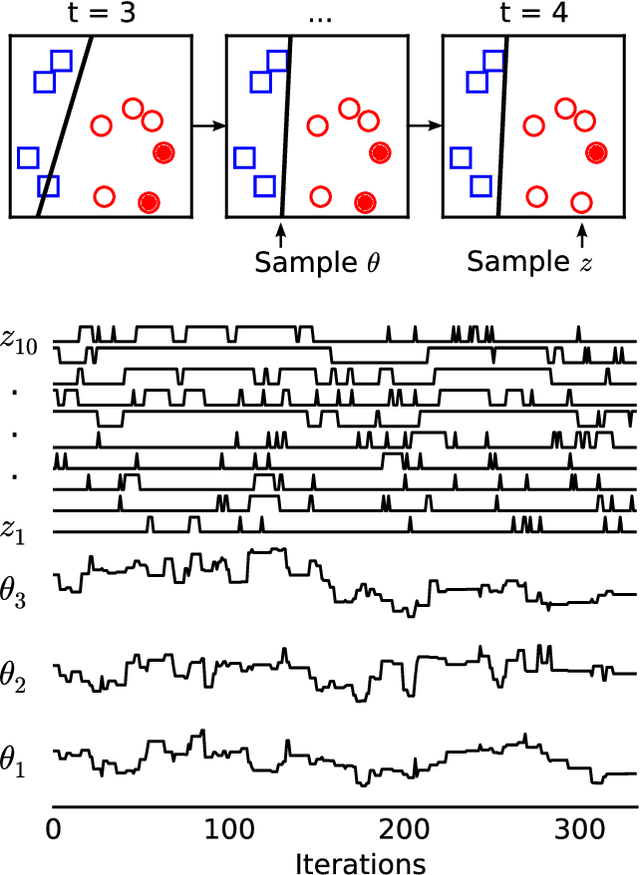
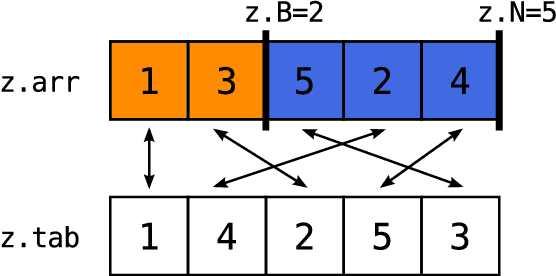
Markov chain Monte Carlo (MCMC) is a popular and successful general-purpose tool for Bayesian inference. However, MCMC cannot be practically applied to large data sets because of the prohibitive cost of evaluating every likelihood term at every iteration. Here we present Firefly Monte Carlo (FlyMC) an auxiliary variable MCMC algorithm that only queries the likelihoods of a potentially small subset of the data at each iteration yet simulates from the exact posterior distribution, in contrast to recent proposals that are approximate even in the asymptotic limit. FlyMC is compatible with a wide variety of modern MCMC algorithms, and only requires a lower bound on the per-datum likelihood factors. In experiments, we find that FlyMC generates samples from the posterior more than an order of magnitude faster than regular MCMC, opening up MCMC methods to larger datasets than were previously considered feasible.