How far away are truly hyperparameter-free learning algorithms?

Despite major advances in methodology, hyperparameter tuning remains a crucial (and expensive) part of the development of machine learning systems. Even ignoring architectural choices, deep neural networks have a large number of optimization and regularization hyperparameters that need to be tuned carefully per workload in order to obtain the best results. In a perfect world, training algorithms would not require workload-specific hyperparameter tuning, but would instead have default settings that performed well across many workloads. Recently, there has been a growing literature on optimization methods which attempt to reduce the number of hyperparameters -- particularly the learning rate and its accompanying schedule. Given these developments, how far away is the dream of neural network training algorithms that completely obviate the need for painful tuning? In this paper, we evaluate the potential of learning-rate-free methods as components of hyperparameter-free methods. We freeze their (non-learning rate) hyperparameters to default values, and score their performance using the recently-proposed AlgoPerf: Training Algorithms benchmark. We found that literature-supplied default settings performed poorly on the benchmark, so we performed a search for hyperparameter configurations that performed well across all workloads simultaneously. The best AlgoPerf-calibrated learning-rate-free methods had much improved performance but still lagged slightly behind a similarly calibrated NadamW baseline in overall benchmark score. Our results suggest that there is still much room for improvement for learning-rate-free methods, and that testing against a strong, workload-agnostic baseline is important to improve hyperparameter reduction techniques.

Unlearning in- vs. out-of-distribution data in LLMs under gradient-based method

Machine unlearning aims to solve the problem of removing the influence of selected training examples from a learned model. Despite the increasing attention to this problem, it remains an open research question how to evaluate unlearning in large language models (LLMs), and what are the critical properties of the data to be unlearned that affect the quality and efficiency of unlearning. This work formalizes a metric to evaluate unlearning quality in generative models, and uses it to assess the trade-offs between unlearning quality and performance. We demonstrate that unlearning out-of-distribution examples requires more unlearning steps but overall presents a better trade-off overall. For in-distribution examples, however, we observe a rapid decay in performance as unlearning progresses. We further evaluate how example's memorization and difficulty affect unlearning under a classical gradient ascent-based approach.

Stepping on the Edge: Curvature Aware Learning Rate Tuners

Curvature information -- particularly, the largest eigenvalue of the loss Hessian, known as the sharpness -- often forms the basis for learning rate tuners. However, recent work has shown that the curvature information undergoes complex dynamics during training, going from a phase of increasing sharpness to eventual stabilization. We analyze the closed-loop feedback effect between learning rate tuning and curvature. We find that classical learning rate tuners may yield greater one-step loss reduction, yet they ultimately underperform in the long term when compared to constant learning rates in the full batch regime. These models break the stabilization of the sharpness, which we explain using a simplified model of the joint dynamics of the learning rate and the curvature. To further investigate these effects, we introduce a new learning rate tuning method, Curvature Dynamics Aware Tuning (CDAT), which prioritizes long term curvature stabilization over instantaneous progress on the objective. In the full batch regime, CDAT shows behavior akin to prefixed warm-up schedules on deep learning objectives, outperforming tuned constant learning rates. In the mini batch regime, we observe that stochasticity introduces confounding effects that explain the previous success of some learning rate tuners at appropriate batch sizes. Our findings highlight the critical role of understanding the joint dynamics of the learning rate and curvature, beyond greedy minimization, to diagnose failures and design effective adaptive learning rate tuners.

Are we making progress in unlearning? Findings from the first NeurIPS unlearning competition

We present the findings of the first NeurIPS competition on unlearning, which sought to stimulate the development of novel algorithms and initiate discussions on formal and robust evaluation methodologies. The competition was highly successful: nearly 1,200 teams from across the world participated, and a wealth of novel, imaginative solutions with different characteristics were contributed. In this paper, we analyze top solutions and delve into discussions on benchmarking unlearning, which itself is a research problem. The evaluation methodology we developed for the competition measures forgetting quality according to a formal notion of unlearning, while incorporating model utility for a holistic evaluation. We analyze the effectiveness of different instantiations of this evaluation framework vis-a-vis the associated compute cost, and discuss implications for standardizing evaluation. We find that the ranking of leading methods remains stable under several variations of this framework, pointing to avenues for reducing the cost of evaluation. Overall, our findings indicate progress in unlearning, with top-performing competition entries surpassing existing algorithms under our evaluation framework. We analyze trade-offs made by different algorithms and strengths or weaknesses in terms of generalizability to new datasets, paving the way for advancing both benchmarking and algorithm development in this important area.

Stability-Aware Training of Neural Network Interatomic Potentials with Differentiable Boltzmann Estimators

Neural network interatomic potentials (NNIPs) are an attractive alternative to ab-initio methods for molecular dynamics (MD) simulations. However, they can produce unstable simulations which sample unphysical states, limiting their usefulness for modeling phenomena occurring over longer timescales. To address these challenges, we present Stability-Aware Boltzmann Estimator (StABlE) Training, a multi-modal training procedure which combines conventional supervised training from quantum-mechanical energies and forces with reference system observables, to produce stable and accurate NNIPs. StABlE Training iteratively runs MD simulations to seek out unstable regions, and corrects the instabilities via supervision with a reference observable. The training procedure is enabled by the Boltzmann Estimator, which allows efficient computation of gradients required to train neural networks to system observables, and can detect both global and local instabilities. We demonstrate our methodology across organic molecules, tetrapeptides, and condensed phase systems, along with using three modern NNIP architectures. In all three cases, StABlE-trained models achieve significant improvements in simulation stability and recovery of structural and dynamic observables. In some cases, StABlE-trained models outperform conventional models trained on datasets 50 times larger. As a general framework applicable across NNIP architectures and systems, StABlE Training is a powerful tool for training stable and accurate NNIPs, particularly in the absence of large reference datasets.

On the Interplay Between Stepsize Tuning and Progressive Sharpening

Recent empirical work has revealed an intriguing property of deep learning models by which the sharpness (largest eigenvalue of the Hessian) increases throughout optimization until it stabilizes around a critical value at which the optimizer operates at the edge of stability, given a fixed stepsize (Cohen et al, 2022). We investigate empirically how the sharpness evolves when using stepsize-tuners, the Armijo linesearch and Polyak stepsizes, that adapt the stepsize along the iterations to local quantities such as, implicitly, the sharpness itself. We find that the surprisingly poor performance of a classical Armijo linesearch may be well explained by its tendency to ever-increase the sharpness of the objective in the full or large batch regimes. On the other hand, we observe that Polyak stepsizes operate generally at the edge of stability or even slightly beyond, while outperforming its Armijo and constant stepsizes counterparts. We conclude with an analysis that suggests unlocking stepsize tuners requires an understanding of the joint dynamics of the step size and the sharpness.

On Implicit Bias in Overparameterized Bilevel Optimization

Many problems in machine learning involve bilevel optimization (BLO), including hyperparameter optimization, meta-learning, and dataset distillation. Bilevel problems consist of two nested sub-problems, called the outer and inner problems, respectively. In practice, often at least one of these sub-problems is overparameterized. In this case, there are many ways to choose among optima that achieve equivalent objective values. Inspired by recent studies of the implicit bias induced by optimization algorithms in single-level optimization, we investigate the implicit bias of gradient-based algorithms for bilevel optimization. We delineate two standard BLO methods -- cold-start and warm-start -- and show that the converged solution or long-run behavior depends to a large degree on these and other algorithmic choices, such as the hypergradient approximation. We also show that the inner solutions obtained by warm-start BLO can encode a surprising amount of information about the outer objective, even when the outer parameters are low-dimensional. We believe that implicit bias deserves as central a role in the study of bilevel optimization as it has attained in the study of single-level neural net optimization.

A Novel Stochastic Gradient Descent Algorithm for Learning Principal Subspaces

Many machine learning problems encode their data as a matrix with a possibly very large number of rows and columns. In several applications like neuroscience, image compression or deep reinforcement learning, the principal subspace of such a matrix provides a useful, low-dimensional representation of individual data. Here, we are interested in determining the $d$-dimensional principal subspace of a given matrix from sample entries, i.e. from small random submatrices. Although a number of sample-based methods exist for this problem (e.g. Oja's rule \citep{oja1982simplified}), these assume access to full columns of the matrix or particular matrix structure such as symmetry and cannot be combined as-is with neural networks \citep{baldi1989neural}. In this paper, we derive an algorithm that learns a principal subspace from sample entries, can be applied when the approximate subspace is represented by a neural network, and hence can be scaled to datasets with an effectively infinite number of rows and columns. Our method consists in defining a loss function whose minimizer is the desired principal subspace, and constructing a gradient estimate of this loss whose bias can be controlled. We complement our theoretical analysis with a series of experiments on synthetic matrices, the MNIST dataset \citep{lecun2010mnist} and the reinforcement learning domain PuddleWorld \citep{sutton1995generalization} demonstrating the usefulness of our approach.

Extragradient with Positive Momentum is Optimal for Games with Cross-Shaped Jacobian Spectrum

The extragradient method has recently gained increasing attention, due to its convergence behavior on smooth games. In $n$-player differentiable games, the eigenvalues of the Jacobian of the vector field are distributed on the complex plane, exhibiting more convoluted dynamics compared to classical (i.e., single player) minimization. In this work, we take a polynomial-based analysis of the extragradient with momentum for optimizing games with \emph{cross-shaped} Jacobian spectrum on the complex plane. We show two results. First, based on the hyperparameter setup, the extragradient with momentum exhibits three different modes of convergence: when the eigenvalues are distributed $i)$ on the real line, $ii)$ both on the real line along with complex conjugates, and $iii)$ only as complex conjugates. Then, we focus on the case $ii)$, i.e., when the eigenvalues of the Jacobian have \emph{cross-shaped} structure, as observed in training generative adversarial networks. For this problem class, we derive the optimal hyperparameters of the momentum extragradient method, and show that it achieves an accelerated convergence rate.

Second-order regression models exhibit progressive sharpening to the edge of stability

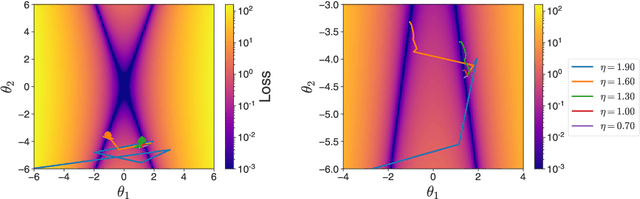
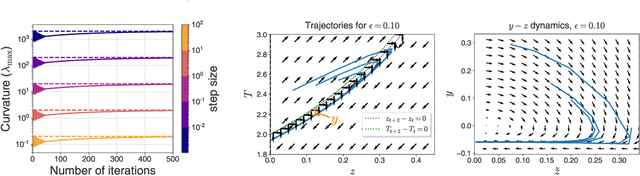
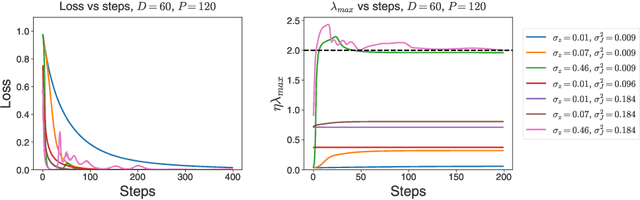
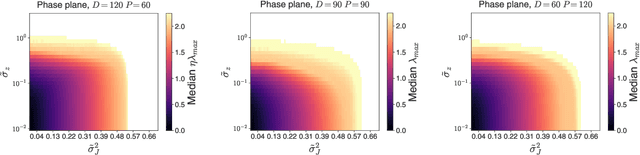
Recent studies of gradient descent with large step sizes have shown that there is often a regime with an initial increase in the largest eigenvalue of the loss Hessian (progressive sharpening), followed by a stabilization of the eigenvalue near the maximum value which allows convergence (edge of stability). These phenomena are intrinsically non-linear and do not happen for models in the constant Neural Tangent Kernel (NTK) regime, for which the predictive function is approximately linear in the parameters. As such, we consider the next simplest class of predictive models, namely those that are quadratic in the parameters, which we call second-order regression models. For quadratic objectives in two dimensions, we prove that this second-order regression model exhibits progressive sharpening of the NTK eigenvalue towards a value that differs slightly from the edge of stability, which we explicitly compute. In higher dimensions, the model generically shows similar behavior, even without the specific structure of a neural network, suggesting that progressive sharpening and edge-of-stability behavior aren't unique features of neural networks, and could be a more general property of discrete learning algorithms in high-dimensional non-linear models.