Hallu-PI: Evaluating Hallucination in Multi-modal Large Language Models within Perturbed Inputs

Multi-modal Large Language Models (MLLMs) have demonstrated remarkable performance on various visual-language understanding and generation tasks. However, MLLMs occasionally generate content inconsistent with the given images, which is known as "hallucination". Prior works primarily center on evaluating hallucination using standard, unperturbed benchmarks, which overlook the prevalent occurrence of perturbed inputs in real-world scenarios-such as image cropping or blurring-that are critical for a comprehensive assessment of MLLMs' hallucination. In this paper, to bridge this gap, we propose Hallu-PI, the first benchmark designed to evaluate Hallucination in MLLMs within Perturbed Inputs. Specifically, Hallu-PI consists of seven perturbed scenarios, containing 1,260 perturbed images from 11 object types. Each image is accompanied by detailed annotations, which include fine-grained hallucination types, such as existence, attribute, and relation. We equip these annotations with a rich set of questions, making Hallu-PI suitable for both discriminative and generative tasks. Extensive experiments on 12 mainstream MLLMs, such as GPT-4V and Gemini-Pro Vision, demonstrate that these models exhibit significant hallucinations on Hallu-PI, which is not observed in unperturbed scenarios. Furthermore, our research reveals a severe bias in MLLMs' ability to handle different types of hallucinations. We also design two baselines specifically for perturbed scenarios, namely Perturbed-Reminder and Perturbed-ICL. We hope that our study will bring researchers' attention to the limitations of MLLMs when dealing with perturbed inputs, and spur further investigations to address this issue. Our code and datasets are publicly available at https://github.com/NJUNLP/Hallu-PI.

Entropy-Reinforced Planning with Large Language Models for Drug Discovery

The objective of drug discovery is to identify chemical compounds that possess specific pharmaceutical properties toward a binding target. Existing large language models (LLMS) can achieve high token matching scores in terms of likelihood for molecule generation. However, relying solely on LLM decoding often results in the generation of molecules that are either invalid due to a single misused token, or suboptimal due to unbalanced exploration and exploitation as a consequence of the LLMs prior experience. Here we propose ERP, Entropy-Reinforced Planning for Transformer Decoding, which employs an entropy-reinforced planning algorithm to enhance the Transformer decoding process and strike a balance between exploitation and exploration. ERP aims to achieve improvements in multiple properties compared to direct sampling from the Transformer. We evaluated ERP on the SARS-CoV-2 virus (3CLPro) and human cancer cell target protein (RTCB) benchmarks and demonstrated that, in both benchmarks, ERP consistently outperforms the current state-of-the-art algorithm by 1-5 percent, and baselines by 5-10 percent, respectively. Moreover, such improvement is robust across Transformer models trained with different objectives. Finally, to further illustrate the capabilities of ERP, we tested our algorithm on three code generation benchmarks and outperformed the current state-of-the-art approach as well. Our code is publicly available at: https://github.com/xuefeng-cs/ERP.

MANGO: A Benchmark for Evaluating Mapping and Navigation Abilities of Large Language Models

Large language models such as ChatGPT and GPT-4 have recently achieved astonishing performance on a variety of natural language processing tasks. In this paper, we propose MANGO, a benchmark to evaluate their capabilities to perform text-based mapping and navigation. Our benchmark includes 53 mazes taken from a suite of textgames: each maze is paired with a walkthrough that visits every location but does not cover all possible paths. The task is question-answering: for each maze, a large language model reads the walkthrough and answers hundreds of mapping and navigation questions such as "How should you go to Attic from West of House?" and "Where are we if we go north and east from Cellar?". Although these questions are easy to humans, it turns out that even GPT-4, the best-to-date language model, performs poorly at answering them. Further, our experiments suggest that a strong mapping and navigation ability would benefit large language models in performing relevant downstream tasks, such as playing textgames. Our MANGO benchmark will facilitate future research on methods that improve the mapping and navigation capabilities of language models. We host our leaderboard, data, code, and evaluation program at https://mango.ttic.edu and https://github.com/oaklight/mango/.

A Wolf in Sheep's Clothing: Generalized Nested Jailbreak Prompts can Fool Large Language Models Easily

Large Language Models (LLMs), such as ChatGPT and GPT-4, are designed to provide useful and safe responses. However, adversarial prompts known as 'jailbreaks' can circumvent safeguards, leading LLMs to generate harmful content. Exploring jailbreak prompts can help to better reveal the weaknesses of LLMs and further steer us to secure them. Unfortunately, existing jailbreak methods either suffer from intricate manual design or require optimization on another white-box model, compromising generalization or jailbreak efficiency. In this paper, we generalize jailbreak prompt attacks into two aspects: (1) Prompt Rewriting and (2) Scenario Nesting. Based on this, we propose ReNeLLM, an automatic framework that leverages LLMs themselves to generate effective jailbreak prompts. Extensive experiments demonstrate that ReNeLLM significantly improves the attack success rate while greatly reducing the time cost compared to existing baselines. Our study also reveals the inadequacy of current defense methods in safeguarding LLMs. Finally, we offer detailed analysis and discussion from the perspective of prompt execution priority on the failure of LLMs' defense. We hope that our research can catalyze both the academic community and LLMs vendors towards the provision of safer and more regulated Large Language Models.

Algebraic and Statistical Properties of the Ordinary Least Squares Interpolator

Deep learning research has uncovered the phenomenon of benign overfitting for over-parameterized statistical models, which has drawn significant theoretical interest in recent years. Given its simplicity and practicality, the ordinary least squares (OLS) interpolator has become essential to gain foundational insights into this phenomenon. While properties of OLS are well established in classical settings, its behavior in high-dimensional settings is less explored (unlike for ridge or lasso regression) though significant progress has been made of late. We contribute to this growing literature by providing fundamental algebraic and statistical results for the minimum $\ell_2$-norm OLS interpolator. In particular, we provide high-dimensional algebraic equivalents of (i) the leave-$k$-out residual formula, (ii) Cochran's formula, and (iii) the Frisch-Waugh-Lovell theorem. These results aid in understanding the OLS interpolator's ability to generalize and have substantive implications for causal inference. Additionally, under the Gauss-Markov model, we present statistical results such as a high-dimensional extension of the Gauss-Markov theorem and an analysis of variance estimation under homoskedastic errors. To substantiate our theoretical contributions, we conduct simulation studies that further explore the stochastic properties of the OLS interpolator.

Regression-Oriented Knowledge Distillation for Lightweight Ship Orientation Angle Prediction with Optical Remote Sensing Images

Ship orientation angle prediction (SOAP) with optical remote sensing images is an important image processing task, which often relies on deep convolutional neural networks (CNNs) to make accurate predictions. This paper proposes a novel framework to reduce the model sizes and computational costs of SOAP models without harming prediction accuracy. First, a new SOAP model called Mobile-SOAP is designed based on MobileNetV2, achieving state-of-the-art prediction accuracy. Four tiny SOAP models are also created by replacing the convolutional blocks in Mobile-SOAP with four small-scale networks, respectively. Then, to transfer knowledge from Mobile-SOAP to four lightweight models, we propose a novel knowledge distillation (KD) framework termed SOAP-KD consisting of a novel feature-based guidance loss and an optimized synthetic samples-based knowledge transfer mechanism. Lastly, extensive experiments on the FGSC-23 dataset confirm the superiority of Mobile-SOAP over existing models and also demonstrate the effectiveness of SOAP-KD in improving the prediction performance of four specially designed tiny models. Notably, by using SOAP-KD, the test mean absolute error of the ShuffleNetV2x1.0-based model is only 8% higher than that of Mobile-SOAP, but its number of parameters and multiply-accumulate operations (MACs) are respectively 61.6% and 60.8% less.

Kernel-based off-policy estimation without overlap: Instance optimality beyond semiparametric efficiency

We study optimal procedures for estimating a linear functional based on observational data. In many problems of this kind, a widely used assumption is strict overlap, i.e., uniform boundedness of the importance ratio, which measures how well the observational data covers the directions of interest. When it is violated, the classical semi-parametric efficiency bound can easily become infinite, so that the instance-optimal risk depends on the function class used to model the regression function. For any convex and symmetric function class $\mathcal{F}$, we derive a non-asymptotic local minimax bound on the mean-squared error in estimating a broad class of linear functionals. This lower bound refines the classical semi-parametric one, and makes connections to moduli of continuity in functional estimation. When $\mathcal{F}$ is a reproducing kernel Hilbert space, we prove that this lower bound can be achieved up to a constant factor by analyzing a computationally simple regression estimator. We apply our general results to various families of examples, thereby uncovering a spectrum of rates that interpolate between the classical theories of semi-parametric efficiency (with $\sqrt{n}$-consistency) and the slower minimax rates associated with non-parametric function estimation.

Multi-Source Causal Inference Using Control Variates

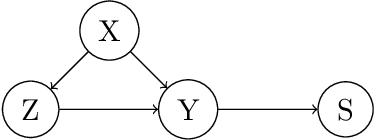
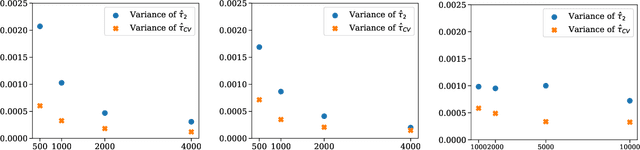
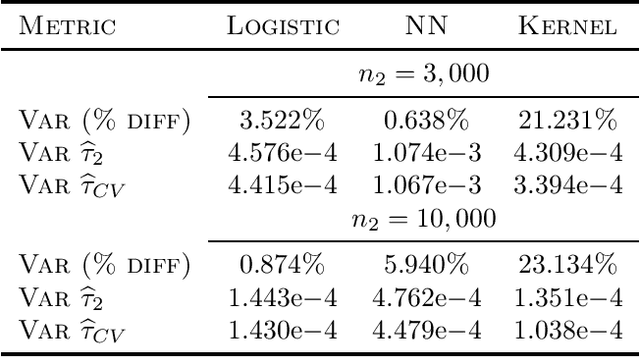
While many areas of machine learning have benefited from the increasing availability of large and varied datasets, the benefit to causal inference has been limited given the strong assumptions needed to ensure identifiability of causal effects; these are often not satisfied in real-world datasets. For example, many large observational datasets (e.g., case-control studies in epidemiology, click-through data in recommender systems) suffer from selection bias on the outcome, which makes the average treatment effect (ATE) unidentifiable. We propose a general algorithm to estimate causal effects from \emph{multiple} data sources, where the ATE may be identifiable only in some datasets but not others. The key idea is to construct control variates using the datasets in which the ATE is not identifiable. We show theoretically that this reduces the variance of the ATE estimate. We apply this framework to inference from observational data under an outcome selection bias, assuming access to an auxiliary small dataset from which we can obtain a consistent estimate of the ATE. We construct a control variate by taking the difference of the odds ratio estimates from the two datasets. Across simulations and two case studies with real data, we show that this control variate can significantly reduce the variance of the ATE estimate.

Conservative Wasserstein Training for Pose Estimation

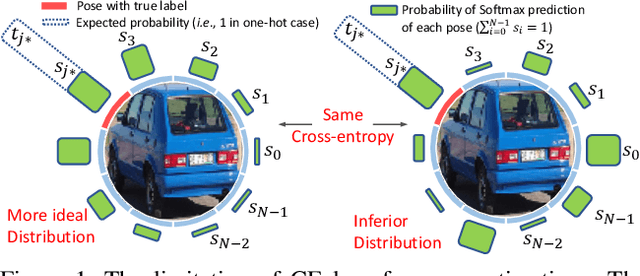
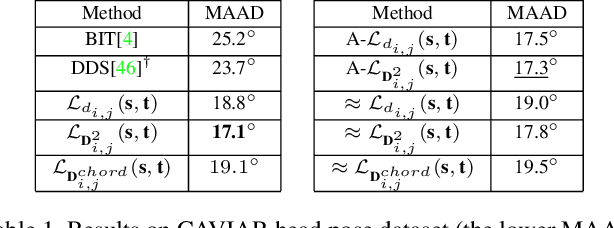
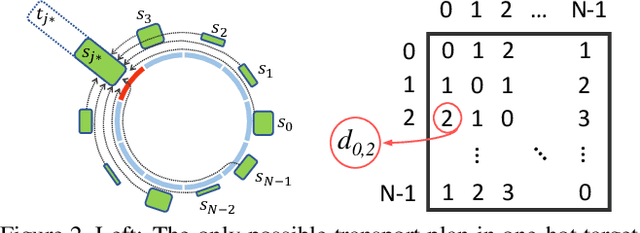
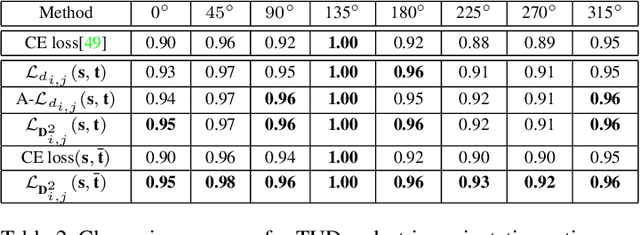
This paper targets the task with discrete and periodic class labels ($e.g.,$ pose/orientation estimation) in the context of deep learning. The commonly used cross-entropy or regression loss is not well matched to this problem as they ignore the periodic nature of the labels and the class similarity, or assume labels are continuous value. We propose to incorporate inter-class correlations in a Wasserstein training framework by pre-defining ($i.e.,$ using arc length of a circle) or adaptively learning the ground metric. We extend the ground metric as a linear, convex or concave increasing function $w.r.t.$ arc length from an optimization perspective. We also propose to construct the conservative target labels which model the inlier and outlier noises using a wrapped unimodal-uniform mixture distribution. Unlike the one-hot setting, the conservative label makes the computation of Wasserstein distance more challenging. We systematically conclude the practical closed-form solution of Wasserstein distance for pose data with either one-hot or conservative target label. We evaluate our method on head, body, vehicle and 3D object pose benchmarks with exhaustive ablation studies. The Wasserstein loss obtaining superior performance over the current methods, especially using convex mapping function for ground metric, conservative label, and closed-form solution.