Efficient Compression of Overparameterized Deep Models through Low-Dimensional Learning Dynamics

Overparameterized models have proven to be powerful tools for solving various machine learning tasks. However, overparameterization often leads to a substantial increase in computational and memory costs, which in turn requires extensive resources to train. In this work, we aim to reduce this complexity by studying the learning dynamics of overparameterized deep networks. By extensively studying its learning dynamics, we unveil that the weight matrices of various architectures exhibit a low-dimensional structure. This finding implies that we can compress the networks by reducing the training to a small subspace. We take a step in developing a principled approach for compressing deep networks by studying deep linear models. We demonstrate that the principal components of deep linear models are fitted incrementally but within a small subspace, and use these insights to compress deep linear networks by decreasing the width of its intermediate layers. Remarkably, we observe that with a particular choice of initialization, the compressed network converges faster than the original network, consistently yielding smaller recovery errors throughout all iterations of gradient descent. We substantiate this observation by developing a theory focused on the deep matrix factorization problem, and by conducting empirical evaluations on deep matrix sensing. Finally, we demonstrate how our compressed model can enhance the utility of deep nonlinear models. Overall, we observe that our compression technique accelerates the training process by more than 2x, without compromising model quality.

Algebraic and Statistical Properties of the Ordinary Least Squares Interpolator

Deep learning research has uncovered the phenomenon of benign overfitting for over-parameterized statistical models, which has drawn significant theoretical interest in recent years. Given its simplicity and practicality, the ordinary least squares (OLS) interpolator has become essential to gain foundational insights into this phenomenon. While properties of OLS are well established in classical settings, its behavior in high-dimensional settings is less explored (unlike for ridge or lasso regression) though significant progress has been made of late. We contribute to this growing literature by providing fundamental algebraic and statistical results for the minimum $\ell_2$-norm OLS interpolator. In particular, we provide high-dimensional algebraic equivalents of (i) the leave-$k$-out residual formula, (ii) Cochran's formula, and (iii) the Frisch-Waugh-Lovell theorem. These results aid in understanding the OLS interpolator's ability to generalize and have substantive implications for causal inference. Additionally, under the Gauss-Markov model, we present statistical results such as a high-dimensional extension of the Gauss-Markov theorem and an analysis of variance estimation under homoskedastic errors. To substantiate our theoretical contributions, we conduct simulation studies that further explore the stochastic properties of the OLS interpolator.

Minimum-Risk Recalibration of Classifiers

Recalibrating probabilistic classifiers is vital for enhancing the reliability and accuracy of predictive models. Despite the development of numerous recalibration algorithms, there is still a lack of a comprehensive theory that integrates calibration and sharpness (which is essential for maintaining predictive power). In this paper, we introduce the concept of minimum-risk recalibration within the framework of mean-squared-error (MSE) decomposition, offering a principled approach for evaluating and recalibrating probabilistic classifiers. Using this framework, we analyze the uniform-mass binning (UMB) recalibration method and establish a finite-sample risk upper bound of order $\tilde{O}(B/n + 1/B^2)$ where $B$ is the number of bins and $n$ is the sample size. By balancing calibration and sharpness, we further determine that the optimal number of bins for UMB scales with $n^{1/3}$, resulting in a risk bound of approximately $O(n^{-2/3})$. Additionally, we tackle the challenge of label shift by proposing a two-stage approach that adjusts the recalibration function using limited labeled data from the target domain. Our results show that transferring a calibrated classifier requires significantly fewer target samples compared to recalibrating from scratch. We validate our theoretical findings through numerical simulations, which confirm the tightness of the proposed bounds, the optimal number of bins, and the effectiveness of label shift adaptation.

Errors-in-variables Fréchet Regression with Low-rank Covariate Approximation

Fr\'echet regression has emerged as a promising approach for regression analysis involving non-Euclidean response variables. However, its practical applicability has been hindered by its reliance on ideal scenarios with abundant and noiseless covariate data. In this paper, we present a novel estimation method that tackles these limitations by leveraging the low-rank structure inherent in the covariate matrix. Our proposed framework combines the concepts of global Fr\'echet regression and principal component regression, aiming to improve the efficiency and accuracy of the regression estimator. By incorporating the low-rank structure, our method enables more effective modeling and estimation, particularly in high-dimensional and errors-in-variables regression settings. We provide a theoretical analysis of the proposed estimator's large-sample properties, including a comprehensive rate analysis of bias, variance, and additional variations due to measurement errors. Furthermore, our numerical experiments provide empirical evidence that supports the theoretical findings, demonstrating the superior performance of our approach. Overall, this work introduces a promising framework for regression analysis of non-Euclidean variables, effectively addressing the challenges associated with limited and noisy covariate data, with potential applications in diverse fields.

Robustness-preserving Lifelong Learning via Dataset Condensation

Lifelong learning (LL) aims to improve a predictive model as the data source evolves continuously. Most work in this learning paradigm has focused on resolving the problem of 'catastrophic forgetting,' which refers to a notorious dilemma between improving model accuracy over new data and retaining accuracy over previous data. Yet, it is also known that machine learning (ML) models can be vulnerable in the sense that tiny, adversarial input perturbations can deceive the models into producing erroneous predictions. This motivates the research objective of this paper - specification of a new LL framework that can salvage model robustness (against adversarial attacks) from catastrophic forgetting. Specifically, we propose a new memory-replay LL strategy that leverages modern bi-level optimization techniques to determine the 'coreset' of the current data (i.e., a small amount of data to be memorized) for ease of preserving adversarial robustness over time. We term the resulting LL framework 'Data-Efficient Robustness-Preserving LL' (DERPLL). The effectiveness of DERPLL is evaluated for class-incremental image classification using ResNet-18 over the CIFAR-10 dataset. Experimental results show that DERPLL outperforms the conventional coreset-guided LL baseline and achieves a substantial improvement in both standard accuracy and robust accuracy.

Sample Efficient Reinforcement Learning via Low-Rank Matrix Estimation

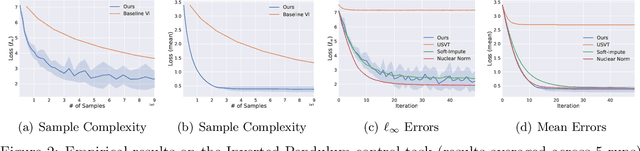
We consider the question of learning $Q$-function in a sample efficient manner for reinforcement learning with continuous state and action spaces under a generative model. If $Q$-function is Lipschitz continuous, then the minimal sample complexity for estimating $\epsilon$-optimal $Q$-function is known to scale as ${\Omega}(\frac{1}{\epsilon^{d_1+d_2 +2}})$ per classical non-parametric learning theory, where $d_1$ and $d_2$ denote the dimensions of the state and action spaces respectively. The $Q$-function, when viewed as a kernel, induces a Hilbert-Schmidt operator and hence possesses square-summable spectrum. This motivates us to consider a parametric class of $Q$-functions parameterized by its "rank" $r$, which contains all Lipschitz $Q$-functions as $r \to \infty$. As our key contribution, we develop a simple, iterative learning algorithm that finds $\epsilon$-optimal $Q$-function with sample complexity of $\widetilde{O}(\frac{1}{\epsilon^{\max(d_1, d_2)+2}})$ when the optimal $Q$-function has low rank $r$ and the discounting factor $\gamma$ is below a certain threshold. Thus, this provides an exponential improvement in sample complexity. To enable our result, we develop a novel Matrix Estimation algorithm that faithfully estimates an unknown low-rank matrix in the $\ell_\infty$ sense even in the presence of arbitrary bounded noise, which might be of interest in its own right. Empirical results on several stochastic control tasks confirm the efficacy of our "low-rank" algorithms.

Model Agnostic High-Dimensional Error-in-Variable Regression

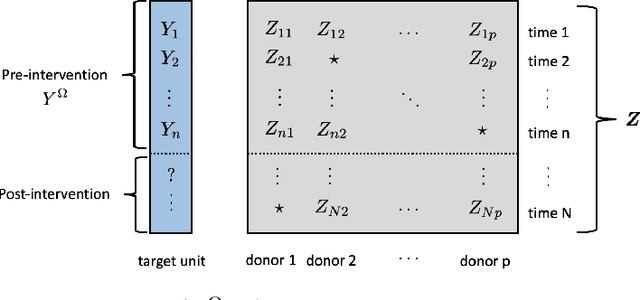
We consider the problem of high-dimensional error-in-variable regression where we only observe a sparse, noisy version of the covariate data. We propose an algorithm that utilizes matrix estimation (ME) as a key subroutine to de-noise the corrupted data, and then performs ordinary least squares regression. When the ME subroutine is instantiated with hard singular value thresholding (HSVT), our results indicate that if the number of samples scales as $\omega( \rho^{-4} r \log^5 (p))$, then our in- and out-of-sample prediction error decays to $0$ as $p \rightarrow \infty$; $\rho$ represents the fraction of observed data, $r$ is the (approximate) rank of the true covariate matrix, and $p$ is the number of covariates. As an important byproduct of our approach, we demonstrate that HSVT with regression acts as implicit $\ell_0$-regularization since HSVT aims to find a low-rank structure within the covariance matrix. Thus, we can view the sparsity of the estimated parameter as a consequence of the covariate structure rather than a model assumption as is often considered in the literature. Moreover, our non-asymptotic bounds match (up to $\log^4(p)$ factors) the best guaranteed sample complexity results in the literature for algorithms that require precise knowledge of the underlying model; we highlight that our approach is model agnostic. In our analysis, we obtain two technical results of independent interest: first, we provide a simple bound on the spectral norm of random matrices with independent sub-exponential rows with randomly missing entries; second, we bound the max column sum error -- a nonstandard error metric -- for HSVT. Our setting enables us to apply our results to applications such as synthetic control for causal inference, time series analysis, and regression with privacy. It is important to note that the existing inventory of methods is unable to analyze these applications.

Learning Mixture Model with Missing Values and its Application to Rankings

We consider the question of learning mixtures of generic sub-gaussian distributions based on observations with missing values. To that end, we utilize a matrix estimation method from literature (soft- or hard- singular value thresholding). Specifically, we stack the observations (with missing values) to form a data matrix and learn a low-rank approximation of it so that the row indices can be correctly clustered to belong to appropriate mixture component using a simple distance-based algorithm. To analyze the performance of this algorithm by quantifying finite sample bound, we extend the result for matrix estimation methods in the literature in two important ways: one, noise across columns is correlated and not independent across all entries of matrix as considered in the literature; two, the performance metric of interest is the maximum l2 row norm error, which is stronger than the traditional mean-squared-error averaged over all entries. Equipped with these advances in the context of matrix estimation, we are able to connect matrix estimation and mixture model learning in the presence of missing data.