Algebraic and Statistical Properties of the Ordinary Least Squares Interpolator

Deep learning research has uncovered the phenomenon of benign overfitting for over-parameterized statistical models, which has drawn significant theoretical interest in recent years. Given its simplicity and practicality, the ordinary least squares (OLS) interpolator has become essential to gain foundational insights into this phenomenon. While properties of OLS are well established in classical settings, its behavior in high-dimensional settings is less explored (unlike for ridge or lasso regression) though significant progress has been made of late. We contribute to this growing literature by providing fundamental algebraic and statistical results for the minimum $\ell_2$-norm OLS interpolator. In particular, we provide high-dimensional algebraic equivalents of (i) the leave-$k$-out residual formula, (ii) Cochran's formula, and (iii) the Frisch-Waugh-Lovell theorem. These results aid in understanding the OLS interpolator's ability to generalize and have substantive implications for causal inference. Additionally, under the Gauss-Markov model, we present statistical results such as a high-dimensional extension of the Gauss-Markov theorem and an analysis of variance estimation under homoskedastic errors. To substantiate our theoretical contributions, we conduct simulation studies that further explore the stochastic properties of the OLS interpolator.

Causal Matrix Completion

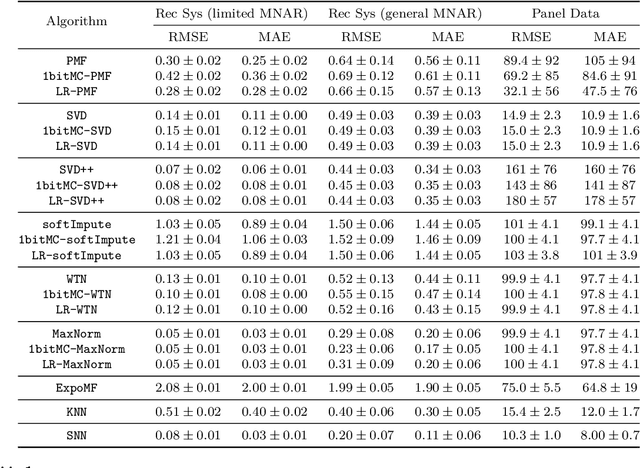
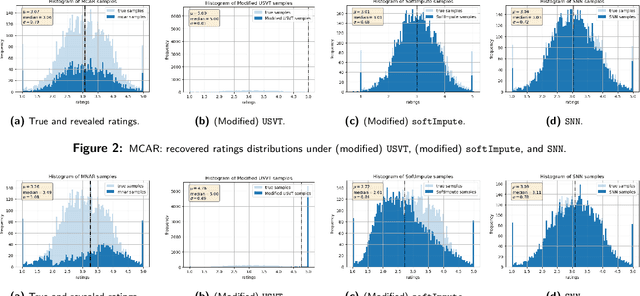
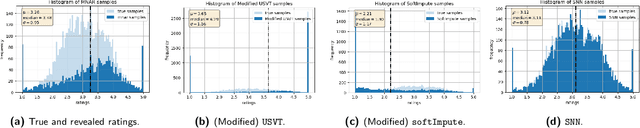
Matrix completion is the study of recovering an underlying matrix from a sparse subset of noisy observations. Traditionally, it is assumed that the entries of the matrix are "missing completely at random" (MCAR), i.e., each entry is revealed at random, independent of everything else, with uniform probability. This is likely unrealistic due to the presence of "latent confounders", i.e., unobserved factors that determine both the entries of the underlying matrix and the missingness pattern in the observed matrix. For example, in the context of movie recommender systems -- a canonical application for matrix completion -- a user who vehemently dislikes horror films is unlikely to ever watch horror films. In general, these confounders yield "missing not at random" (MNAR) data, which can severely impact any inference procedure that does not correct for this bias. We develop a formal causal model for matrix completion through the language of potential outcomes, and provide novel identification arguments for a variety of causal estimands of interest. We design a procedure, which we call "synthetic nearest neighbors" (SNN), to estimate these causal estimands. We prove finite-sample consistency and asymptotic normality of our estimator. Our analysis also leads to new theoretical results for the matrix completion literature. In particular, we establish entry-wise, i.e., max-norm, finite-sample consistency and asymptotic normality results for matrix completion with MNAR data. As a special case, this also provides entry-wise bounds for matrix completion with MCAR data. Across simulated and real data, we demonstrate the efficacy of our proposed estimator.

PerSim: Data-Efficient Offline Reinforcement Learning with Heterogeneous Agents via Personalized Simulators

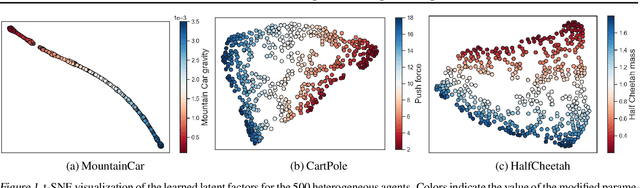
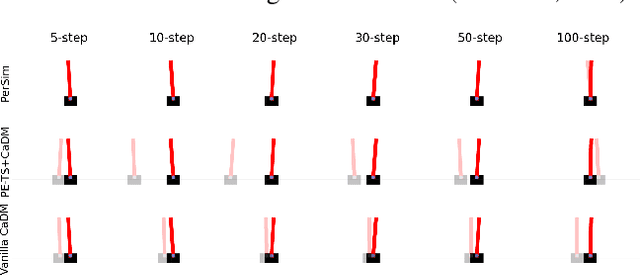
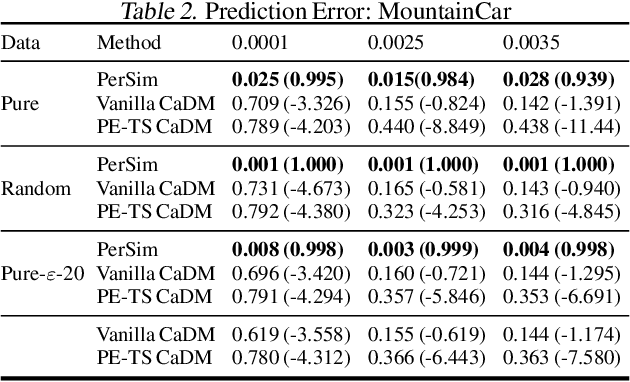
We consider offline reinforcement learning (RL) with heterogeneous agents under severe data scarcity, i.e., we only observe a single historical trajectory for every agent under an unknown, potentially sub-optimal policy. We find that the performance of state-of-the-art offline and model-based RL methods degrade significantly given such limited data availability, even for commonly perceived "solved" benchmark settings such as "MountainCar" and "CartPole". To address this challenge, we propose a model-based offline RL approach, called PerSim, where we first learn a personalized simulator for each agent by collectively using the historical trajectories across all agents prior to learning a policy. We do so by positing that the transition dynamics across agents can be represented as a latent function of latent factors associated with agents, states, and actions; subsequently, we theoretically establish that this function is well-approximated by a "low-rank" decomposition of separable agent, state, and action latent functions. This representation suggests a simple, regularized neural network architecture to effectively learn the transition dynamics per agent, even with scarce, offline data.We perform extensive experiments across several benchmark environments and RL methods. The consistent improvement of our approach, measured in terms of state dynamics prediction and eventual reward, confirms the efficacy of our framework in leveraging limited historical data to simultaneously learn personalized policies across agents.

On Principal Component Regression in a High-Dimensional Error-in-Variables Setting

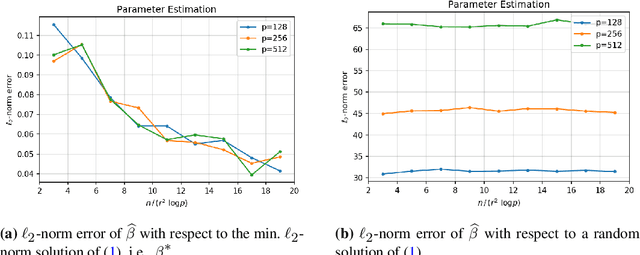
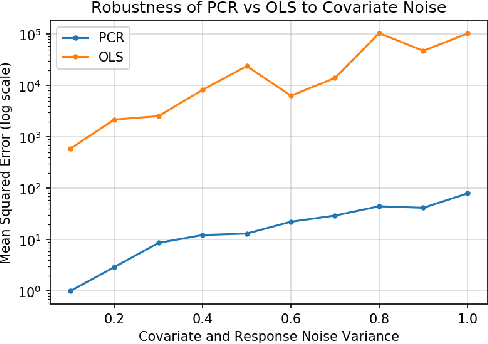
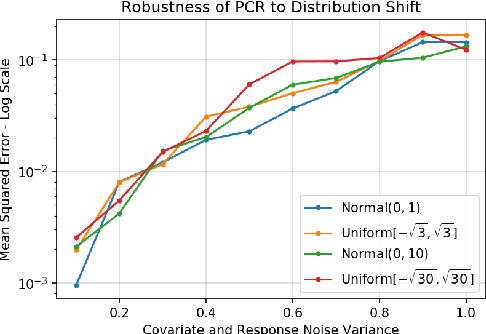
We analyze the classical method of Principal Component Regression (PCR) in the high-dimensional error-in-variables setting. Here, the observed covariates are not only noisy and contain missing data, but the number of covariates can also exceed the sample size. Under suitable conditions, we establish that PCR identifies the unique model parameter with minimum $\ell_2$-norm, and derive non-asymptotic $\ell_2$-rates of convergence that show its consistency. We further provide non-asymptotic out-of-sample prediction performance guarantees that again prove consistency, even in the presence of corrupted unseen data. Notably, our results do not require the out-of-samples covariates to follow the same distribution as that of the in-sample covariates, but rather that they obey a simple linear algebraic constraint. We finish by presenting simulations that illustrate our theoretical results.

Synthetic Interventions

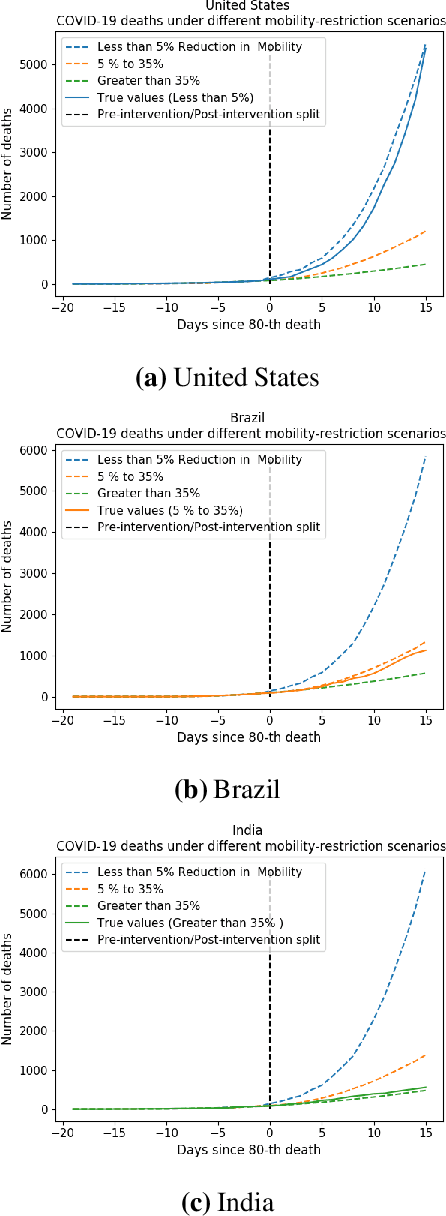
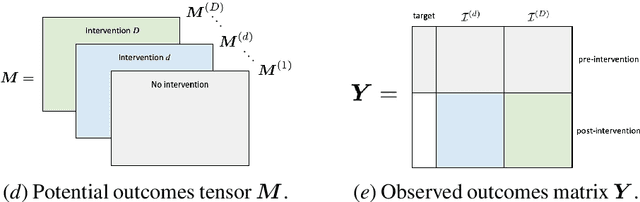
We develop a method to help quantify the impact different levels of mobility restrictions could have had on COVID-19 related deaths across nations. Synthetic control (SC) has emerged as a standard tool in such scenarios to produce counterfactual estimates if a particular intervention had not occurred, using just observational data. However, it remains an important open problem of how to extend SC to obtain counterfactual estimates if a particular intervention had occurred - this is exactly the question of the impact of mobility restrictions stated above. As our main contribution, we introduce synthetic interventions (SI), which helps resolve this open problem by allowing one to produce counterfactual estimates if there are multiple interventions of interest. We prove SI produces consistent counterfactual estimates under a tensor factor model. Our finite sample analysis shows the test error decays as $1/T_0$, where $T_0$ is the amount of observed pre-intervention data. As a special case, this improves upon the $1/\sqrt{T_0}$ bound on test error for SC in prior works. Our test error bound holds under a certain "subspace inclusion" condition; we furnish a data-driven hypothesis test with provable guarantees to check for this condition. This also provides a quantitative hypothesis test for when to use SC, currently absent in the literature. Technically, we establish the parameter estimation and test error for Principal Component Regression (a key subroutine in SI and several SC variants) under the setting of error-in-variable regression decays as $1/T_0$, where $T_0$ is the number of samples observed; this improves the best prior test error bound of $1/\sqrt{T_0}$. In addition to the COVID-19 case study, we show how SI can be used to run data-efficient, personalized randomized control trials using real data from a large e-commerce website and a large developmental economics study.

Two Burning Questions on COVID-19: Did shutting down the economy help? Can we reopen the economy without risking the second wave?

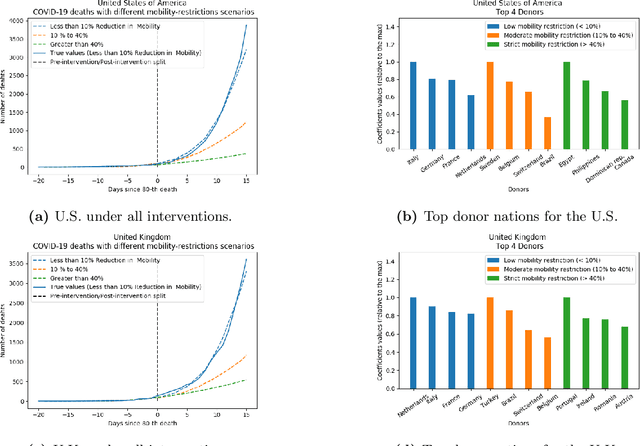
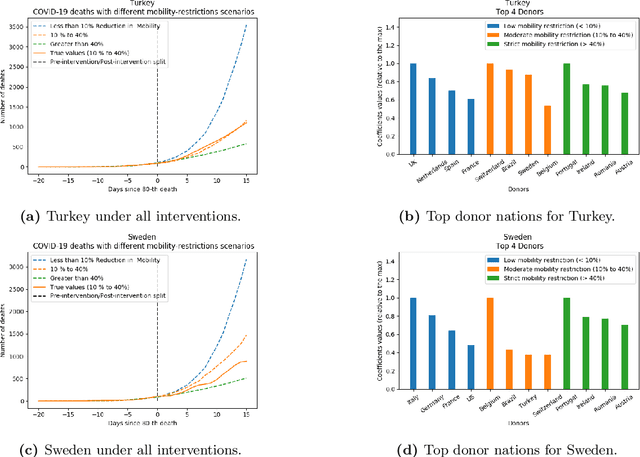
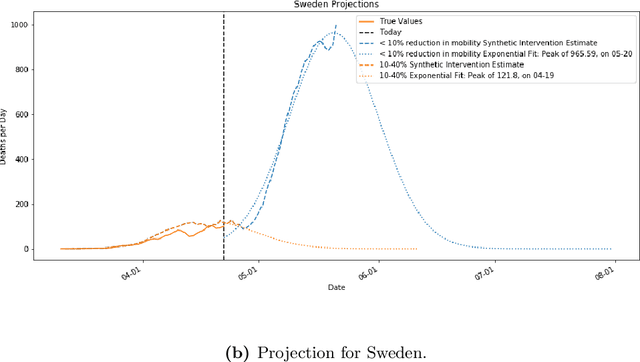
As we reach the apex of the COVID-19 pandemic, the most pressing question facing us is: can we even partially reopen the economy without risking a second wave? We first need to understand if shutting down the economy helped. And if it did, is it possible to achieve similar gains in the war against the pandemic while partially opening up the economy? To do so, it is critical to understand the effects of the various interventions that can be put into place and their corresponding health and economic implications. Since many interventions exist, the key challenge facing policy makers is understanding the potential trade-offs between them, and choosing the particular set of interventions that works best for their circumstance. In this memo, we provide an overview of Synthetic Interventions (a natural generalization of Synthetic Control), a data-driven and statistically principled method to perform what-if scenario planning, i.e., for policy makers to understand the trade-offs between different interventions before having to actually enact them. In essence, the method leverages information from different interventions that have already been enacted across the world and fits it to a policy maker's setting of interest, e.g., to estimate the effect of mobility-restricting interventions on the U.S., we use daily death data from countries that enforced severe mobility restrictions to create a "synthetic low mobility U.S." and predict the counterfactual trajectory of the U.S. if it had indeed applied a similar intervention. Using Synthetic Interventions, we find that lifting severe mobility restrictions and only retaining moderate mobility restrictions (at retail and transit locations), seems to effectively flatten the curve. We hope this provides guidance on weighing the trade-offs between the safety of the population, strain on the healthcare system, and impact on the economy.

Model Agnostic High-Dimensional Error-in-Variable Regression

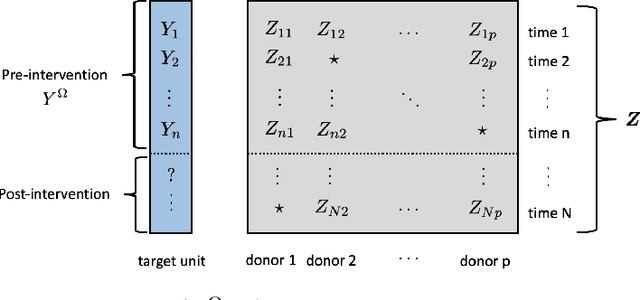
We consider the problem of high-dimensional error-in-variable regression where we only observe a sparse, noisy version of the covariate data. We propose an algorithm that utilizes matrix estimation (ME) as a key subroutine to de-noise the corrupted data, and then performs ordinary least squares regression. When the ME subroutine is instantiated with hard singular value thresholding (HSVT), our results indicate that if the number of samples scales as $\omega( \rho^{-4} r \log^5 (p))$, then our in- and out-of-sample prediction error decays to $0$ as $p \rightarrow \infty$; $\rho$ represents the fraction of observed data, $r$ is the (approximate) rank of the true covariate matrix, and $p$ is the number of covariates. As an important byproduct of our approach, we demonstrate that HSVT with regression acts as implicit $\ell_0$-regularization since HSVT aims to find a low-rank structure within the covariance matrix. Thus, we can view the sparsity of the estimated parameter as a consequence of the covariate structure rather than a model assumption as is often considered in the literature. Moreover, our non-asymptotic bounds match (up to $\log^4(p)$ factors) the best guaranteed sample complexity results in the literature for algorithms that require precise knowledge of the underlying model; we highlight that our approach is model agnostic. In our analysis, we obtain two technical results of independent interest: first, we provide a simple bound on the spectral norm of random matrices with independent sub-exponential rows with randomly missing entries; second, we bound the max column sum error -- a nonstandard error metric -- for HSVT. Our setting enables us to apply our results to applications such as synthetic control for causal inference, time series analysis, and regression with privacy. It is important to note that the existing inventory of methods is unable to analyze these applications.

Time Series Analysis via Matrix Estimation

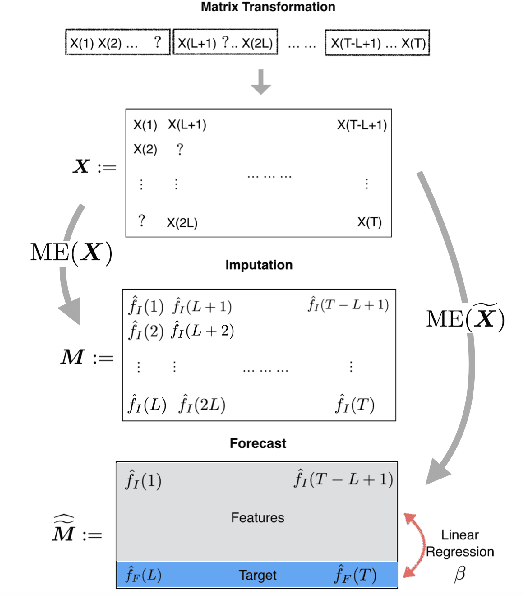
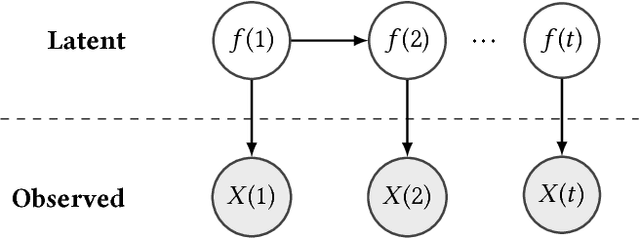
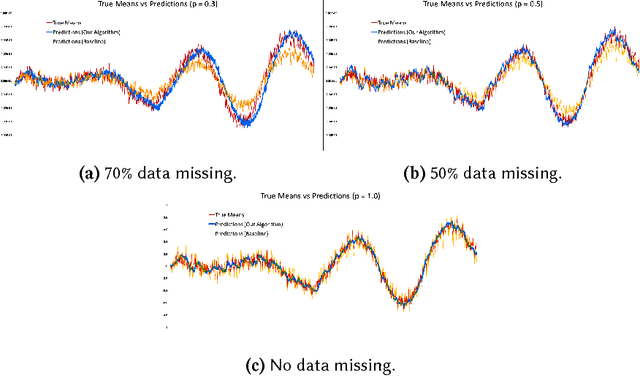
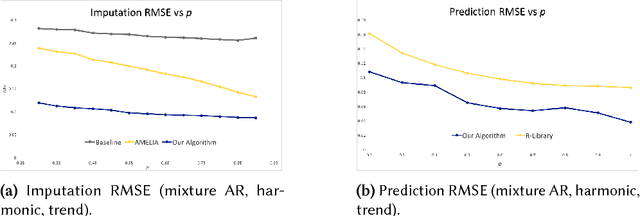
We propose an algorithm to impute and forecast a time series by transforming the observed time series into a matrix, utilizing matrix estimation to recover missing values and de-noise observed entries, and performing linear regression to make predictions. At the core of our analysis is a representation result, which states that for a large model class, the transformed matrix obtained from the time series via our algorithm is (approximately) low-rank. This, in effect, generalizes the widely used Singular Spectrum Analysis (SSA) in literature, and allows us to establish a rigorous link between time series analysis and matrix estimation. The key is to construct a matrix with non-overlapping entries rather than with the Hankel matrix as done in the literature, including in SSA. We provide finite sample analysis for imputation and prediction leading to the asymptotic consistency of our method. A salient feature of our algorithm is that it is model agnostic both with respect to the underlying time dynamics as well as the noise model in the observations. Being noise agnostic makes our algorithm applicable to the setting where the state is hidden and we only have access to its noisy observations a la a Hidden Markov Model, e.g., observing a Poisson process with a time-varying parameter without knowing that the process is Poisson, but still recovering the time-varying parameter accurately. As part of the forecasting algorithm, an important task is to perform regression with noisy observations of the features a la an error- in-variable regression. In essence, our approach suggests a matrix estimation based method for such a setting, which could be of interest in its own right. Through synthetic and real-world datasets, we demonstrate that our algorithm outperforms standard software packages (including R libraries) in the presence of missing data as well as high levels of noise.

Robust Synthetic Control

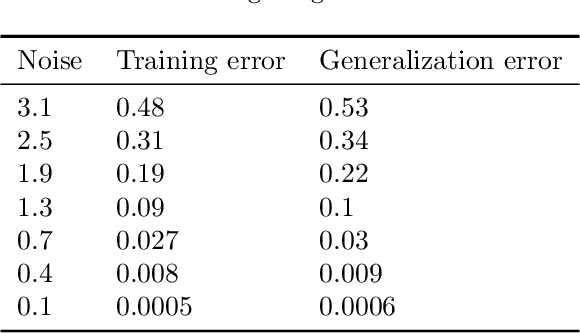
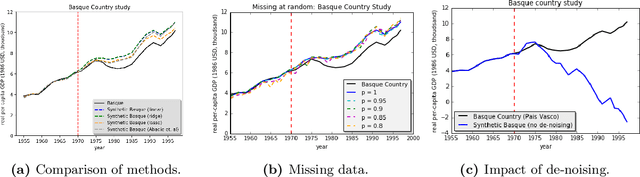
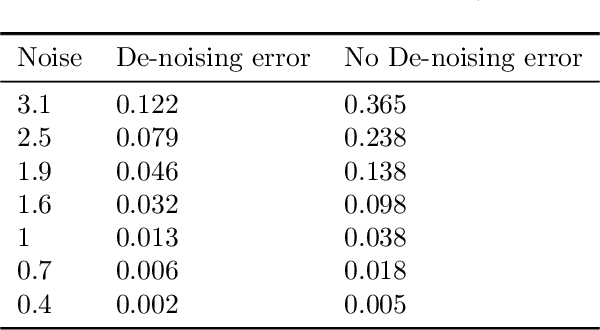
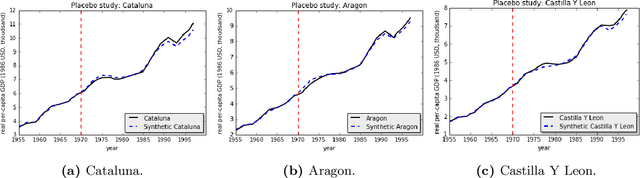
We present a robust generalization of the synthetic control method for comparative case studies. Like the classical method, we present an algorithm to estimate the unobservable counterfactual of a treatment unit. A distinguishing feature of our algorithm is that of de-noising the data matrix via singular value thresholding, which renders our approach robust in multiple facets: it automatically identifies a good subset of donors, overcomes the challenges of missing data, and continues to work well in settings where covariate information may not be provided. To begin, we establish the condition under which the fundamental assumption in synthetic control-like approaches holds, i.e. when the linear relationship between the treatment unit and the donor pool prevails in both the pre- and post-intervention periods. We provide the first finite sample analysis for a broader class of models, the Latent Variable Model, in contrast to Factor Models previously considered in the literature. Further, we show that our de-noising procedure accurately imputes missing entries, producing a consistent estimator of the underlying signal matrix provided $p = \Omega( T^{-1 + \zeta})$ for some $\zeta > 0$; here, $p$ is the fraction of observed data and $T$ is the time interval of interest. Under the same setting, we prove that the mean-squared-error (MSE) in our prediction estimation scales as $O(\sigma^2/p + 1/\sqrt{T})$, where $\sigma^2$ is the noise variance. Using a data aggregation method, we show that the MSE can be made as small as $O(T^{-1/2+\gamma})$ for any $\gamma \in (0, 1/2)$, leading to a consistent estimator. We also introduce a Bayesian framework to quantify the model uncertainty through posterior probabilities. Our experiments, using both real-world and synthetic datasets, demonstrate that our robust generalization yields an improvement over the classical synthetic control method.