Differential Privacy on Trust Graphs

We study differential privacy (DP) in a multi-party setting where each party only trusts a (known) subset of the other parties with its data. Specifically, given a trust graph where vertices correspond to parties and neighbors are mutually trusting, we give a DP algorithm for aggregation with a much better privacy-utility trade-off than in the well-studied local model of DP (where each party trusts no other party). We further study a robust variant where each party trusts all but an unknown subset of at most $t$ of its neighbors (where $t$ is a given parameter), and give an algorithm for this setting. We complement our algorithms with lower bounds, and discuss implications of our work to other tasks in private learning and analytics.

Score Design for Multi-Criteria Incentivization

We present a framework for designing scores to summarize performance metrics. Our design has two multi-criteria objectives: (1) improving on scores should improve all performance metrics, and (2) achieving pareto-optimal scores should achieve pareto-optimal metrics. We formulate our design to minimize the dimensionality of scores while satisfying the objectives. We give algorithms to design scores, which are provably minimal under mild assumptions on the structure of performance metrics. This framework draws motivation from real-world practices in hospital rating systems, where misaligned scores and performance metrics lead to unintended consequences.

Operationalizing Counterfactual Metrics: Incentives, Ranking, and Information Asymmetry

From the social sciences to machine learning, it has been well documented that metrics to be optimized are not always aligned with social welfare. In healthcare, Dranove et al. [12] showed that publishing surgery mortality metrics actually harmed the welfare of sicker patients by increasing provider selection behavior. Using a principal-agent model, we directly study the incentive misalignments that arise from such average treated outcome metrics, and show that the incentives driving treatment decisions would align with maximizing total patient welfare if the metrics (i) accounted for counterfactual untreated outcomes and (ii) considered total welfare instead of average welfare among treated patients. Operationalizing this, we show how counterfactual metrics can be modified to satisfy desirable properties when used for ranking. Extending to realistic settings when the providers observe more about patients than the regulatory agencies do, we bound the decay in performance by the degree of information asymmetry between the principal and the agent. In doing so, our model connects principal-agent information asymmetry with unobserved heterogeneity in causal inference.

Lost in Translation: Reimagining the Machine Learning Life Cycle in Education

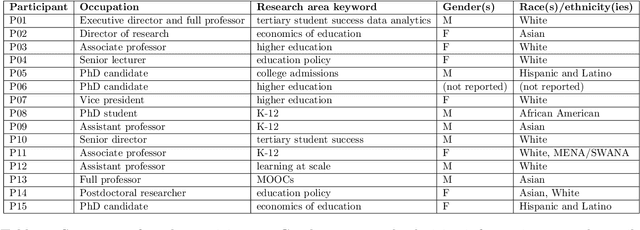
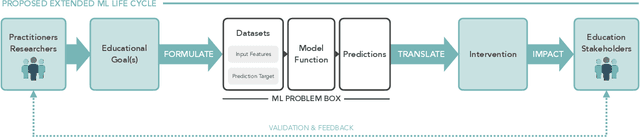
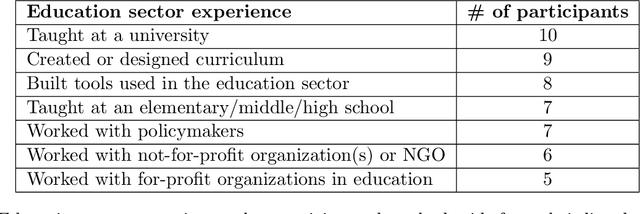
Machine learning (ML) techniques are increasingly prevalent in education, from their use in predicting student dropout, to assisting in university admissions, and facilitating the rise of MOOCs. Given the rapid growth of these novel uses, there is a pressing need to investigate how ML techniques support long-standing education principles and goals. In this work, we shed light on this complex landscape drawing on qualitative insights from interviews with education experts. These interviews comprise in-depth evaluations of ML for education (ML4Ed) papers published in preeminent applied ML conferences over the past decade. Our central research goal is to critically examine how the stated or implied education and societal objectives of these papers are aligned with the ML problems they tackle. That is, to what extent does the technical problem formulation, objectives, approach, and interpretation of results align with the education problem at hand. We find that a cross-disciplinary gap exists and is particularly salient in two parts of the ML life cycle: the formulation of an ML problem from education goals and the translation of predictions to interventions. We use these insights to propose an extended ML life cycle, which may also apply to the use of ML in other domains. Our work joins a growing number of meta-analytical studies across education and ML research, as well as critical analyses of the societal impact of ML. Specifically, it fills a gap between the prevailing technical understanding of machine learning and the perspective of education researchers working with students and in policy.

Robust Distillation for Worst-class Performance

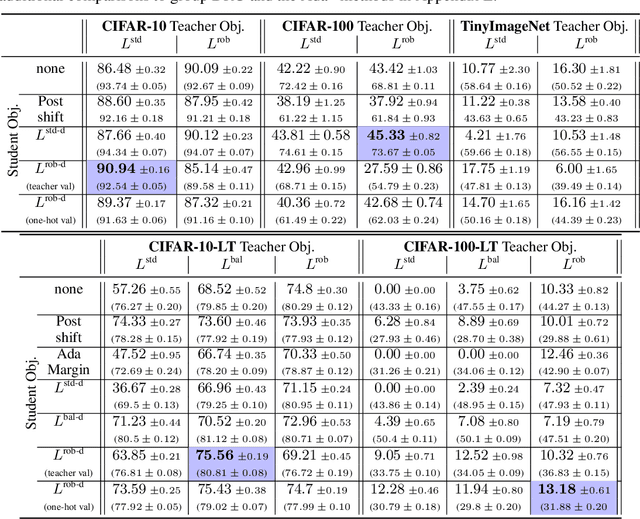
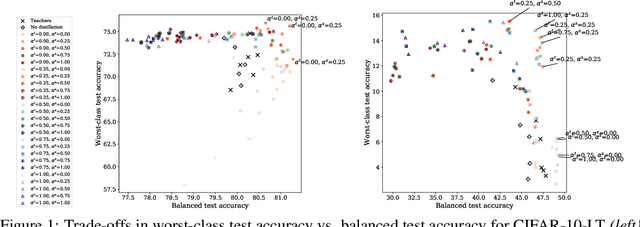
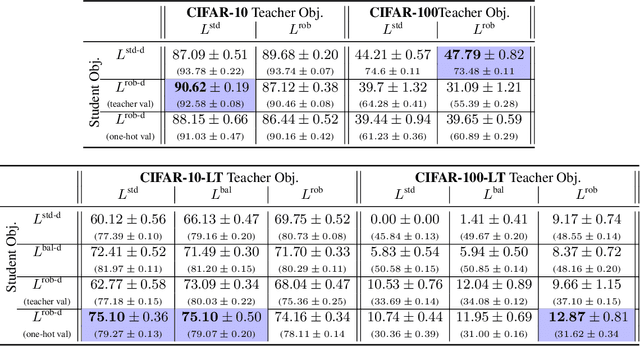
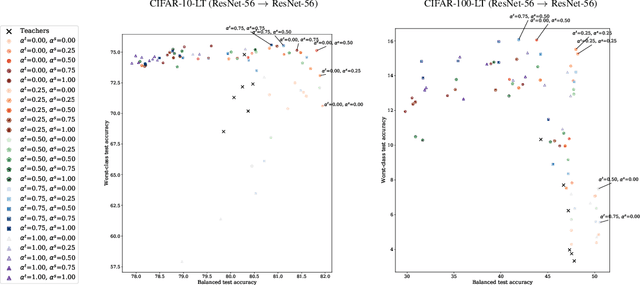
Knowledge distillation has proven to be an effective technique in improving the performance a student model using predictions from a teacher model. However, recent work has shown that gains in average efficiency are not uniform across subgroups in the data, and in particular can often come at the cost of accuracy on rare subgroups and classes. To preserve strong performance across classes that may follow a long-tailed distribution, we develop distillation techniques that are tailored to improve the student's worst-class performance. Specifically, we introduce robust optimization objectives in different combinations for the teacher and student, and further allow for training with any tradeoff between the overall accuracy and the robust worst-class objective. We show empirically that our robust distillation techniques not only achieve better worst-class performance, but also lead to Pareto improvement in the tradeoff between overall performance and worst-class performance compared to other baseline methods. Theoretically, we provide insights into what makes a good teacher when the goal is to train a robust student.

Variational Refinement for Importance Sampling Using the Forward Kullback-Leibler Divergence

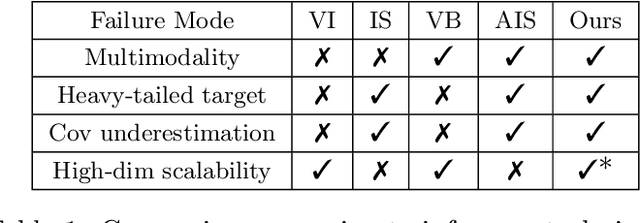
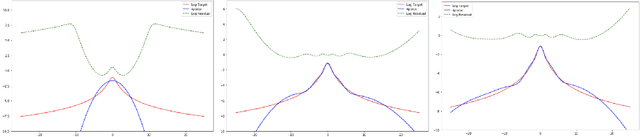
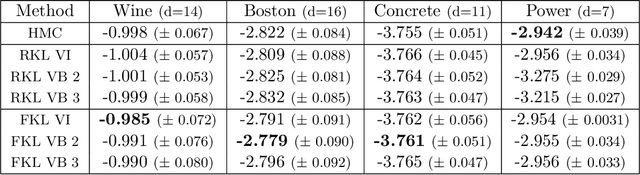
Variational Inference (VI) is a popular alternative to asymptotically exact sampling in Bayesian inference. Its main workhorse is optimization over a reverse Kullback-Leibler divergence (RKL), which typically underestimates the tail of the posterior leading to miscalibration and potential degeneracy. Importance sampling (IS), on the other hand, is often used to fine-tune and de-bias the estimates of approximate Bayesian inference procedures. The quality of IS crucially depends on the choice of the proposal distribution. Ideally, the proposal distribution has heavier tails than the target, which is rarely achievable by minimizing the RKL. We thus propose a novel combination of optimization and sampling techniques for approximate Bayesian inference by constructing an IS proposal distribution through the minimization of a forward KL (FKL) divergence. This approach guarantees asymptotic consistency and a fast convergence towards both the optimal IS estimator and the optimal variational approximation. We empirically demonstrate on real data that our method is competitive with variational boosting and MCMC.

Multi-Source Causal Inference Using Control Variates

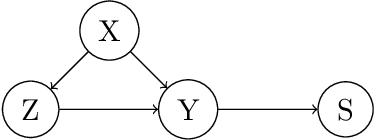
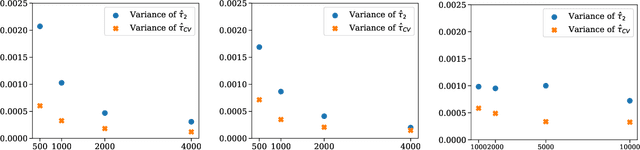
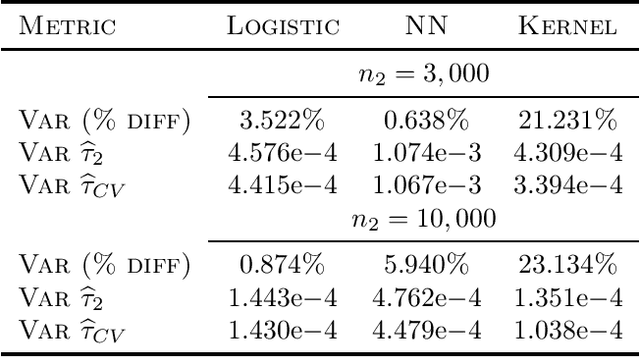
While many areas of machine learning have benefited from the increasing availability of large and varied datasets, the benefit to causal inference has been limited given the strong assumptions needed to ensure identifiability of causal effects; these are often not satisfied in real-world datasets. For example, many large observational datasets (e.g., case-control studies in epidemiology, click-through data in recommender systems) suffer from selection bias on the outcome, which makes the average treatment effect (ATE) unidentifiable. We propose a general algorithm to estimate causal effects from \emph{multiple} data sources, where the ATE may be identifiable only in some datasets but not others. The key idea is to construct control variates using the datasets in which the ATE is not identifiable. We show theoretically that this reduces the variance of the ATE estimate. We apply this framework to inference from observational data under an outcome selection bias, assuming access to an auxiliary small dataset from which we can obtain a consistent estimate of the ATE. We construct a control variate by taking the difference of the odds ratio estimates from the two datasets. Across simulations and two case studies with real data, we show that this control variate can significantly reduce the variance of the ATE estimate.

Regularization Strategies for Quantile Regression

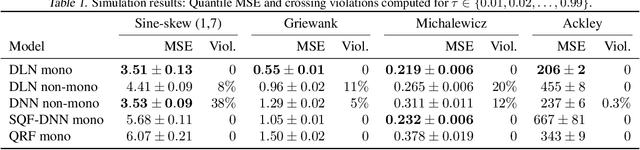
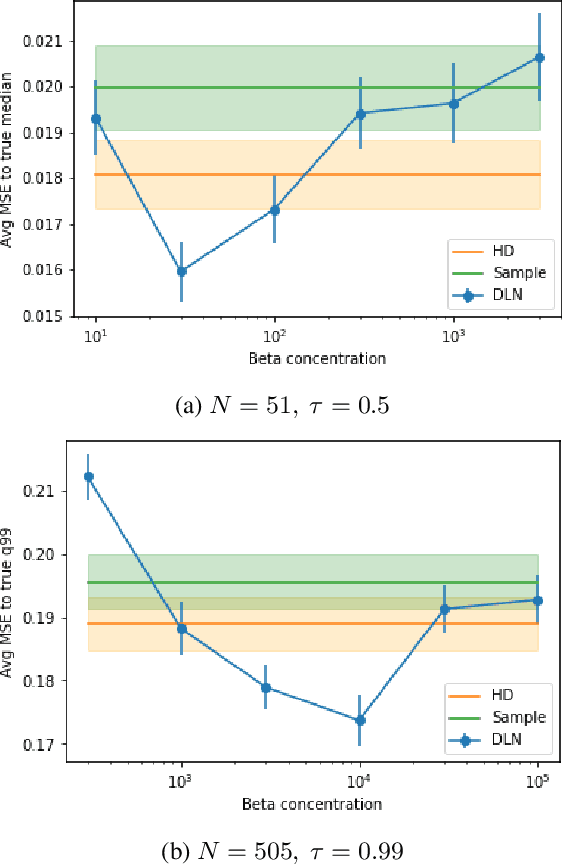
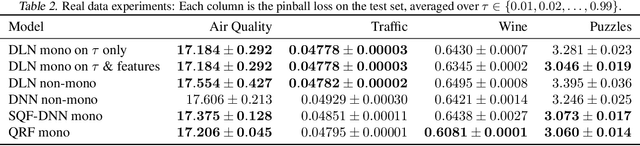
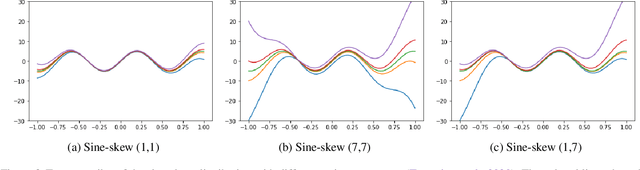
We investigate different methods for regularizing quantile regression when predicting either a subset of quantiles or the full inverse CDF. We show that minimizing an expected pinball loss over a continuous distribution of quantiles is a good regularizer even when only predicting a specific quantile. For predicting multiple quantiles, we propose achieving the classic goal of non-crossing quantiles by using deep lattice networks that treat the quantile as a monotonic input feature, and we discuss why monotonicity on other features is an apt regularizer for quantile regression. We show that lattice models enable regularizing the predicted distribution to a location-scale family. Lastly, we propose applying rate constraints to improve the calibration of the quantile predictions on specific subsets of interest and improve fairness metrics. We demonstrate our contributions on simulations, benchmark datasets, and real quantile regression problems.

Robust Optimization for Fairness with Noisy Protected Groups

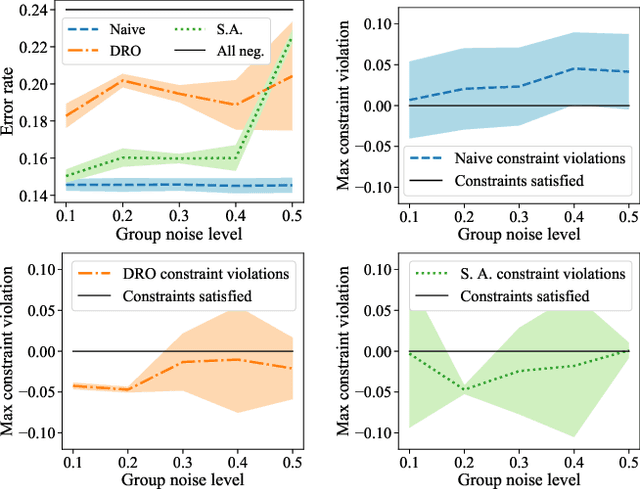
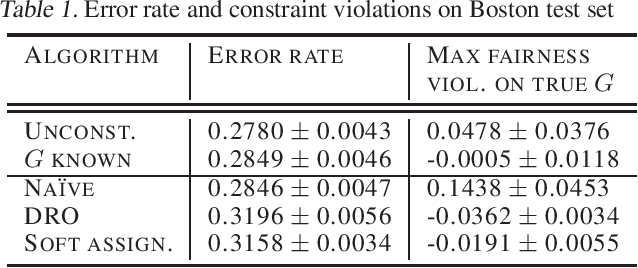
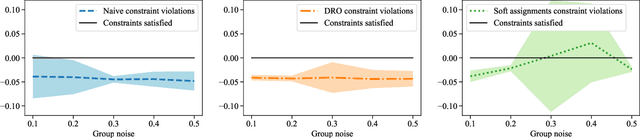
Many existing fairness criteria for machine learning involve equalizing or achieving some metric across \textit{protected groups} such as race or gender groups. However, practitioners trying to audit or enforce such group-based criteria can easily face the problem of noisy or biased protected group information. We study this important practical problem in two ways. First, we study the consequences of na{\"i}vely only relying on noisy protected groups: we provide an upper bound on the fairness violations on the true groups $G$ when the fairness criteria are satisfied on noisy groups $\hat{G}$. Second, we introduce two new approaches using robust optimization that, unlike the na{\"i}ve approach of only relying on $\hat{G}$, are guaranteed to satisfy fairness criteria on the true protected groups $G$ while minimizing a training objective. We provide theoretical guarantees that one such approach converges to an optimal feasible solution. Using two case studies, we empirically show that the robust approaches achieve better true group fairness guarantees than the na{\"i}ve approach.

Deontological Ethics By Monotonicity Shape Constraints

We demonstrate how easy it is for modern machine-learned systems to violate common deontological ethical principles and social norms such as "favor the less fortunate", and "do not penalize good attributes." We propose that in some cases such ethical principles can be incorporated into a machine-learned model by adding shape constraints that constrain the model to respond only positively to relevant inputs. We analyze the relationship between these deontological constraints that act on individuals and the consequentialist group-based fairness goals of one-sided statistical parity and equal opportunity. This strategy works with sensitive attributes that are Boolean or real-valued such as income and age, and can help produce more responsible and trustworthy AI.