Liwei Wang
N3C Natural Language Processing
On the Power of Pre-training for Generalization in RL: Provable Benefits and Hardness
Oct 19, 2022Abstract:Generalization in Reinforcement Learning (RL) aims to learn an agent during training that generalizes to the target environment. This paper studies RL generalization from a theoretical aspect: how much can we expect pre-training over training environments to be helpful? When the interaction with the target environment is not allowed, we certify that the best we can obtain is a near-optimal policy in an average sense, and we design an algorithm that achieves this goal. Furthermore, when the agent is allowed to interact with the target environment, we give a surprising result showing that asymptotically, the improvement from pre-training is at most a constant factor. On the other hand, in the non-asymptotic regime, we design an efficient algorithm and prove a distribution-based regret bound in the target environment that is independent of the state-action space.
CAGroup3D: Class-Aware Grouping for 3D Object Detection on Point Clouds
Oct 09, 2022
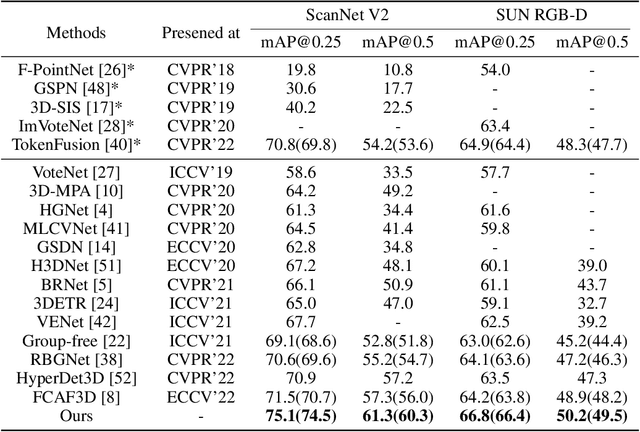
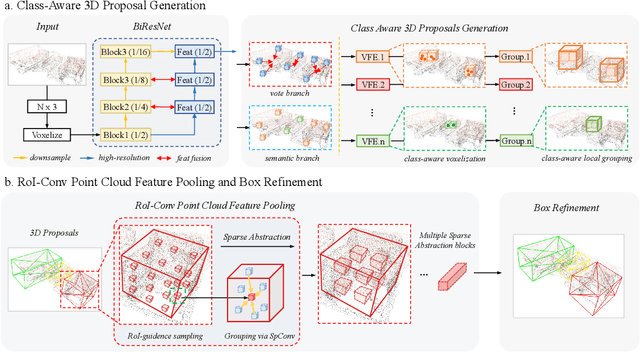

Abstract:We present a novel two-stage fully sparse convolutional 3D object detection framework, named CAGroup3D. Our proposed method first generates some high-quality 3D proposals by leveraging the class-aware local group strategy on the object surface voxels with the same semantic predictions, which considers semantic consistency and diverse locality abandoned in previous bottom-up approaches. Then, to recover the features of missed voxels due to incorrect voxel-wise segmentation, we build a fully sparse convolutional RoI pooling module to directly aggregate fine-grained spatial information from backbone for further proposal refinement. It is memory-and-computation efficient and can better encode the geometry-specific features of each 3D proposal. Our model achieves state-of-the-art 3D detection performance with remarkable gains of +\textit{3.6\%} on ScanNet V2 and +\textit{2.6}\% on SUN RGB-D in term of mAP@0.25. Code will be available at https://github.com/Haiyang-W/CAGroup3D.
One Transformer Can Understand Both 2D & 3D Molecular Data
Oct 04, 2022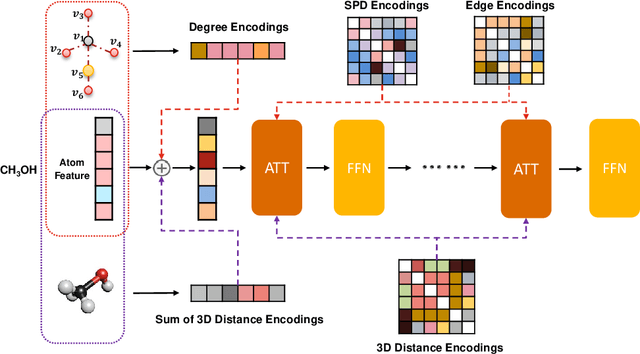
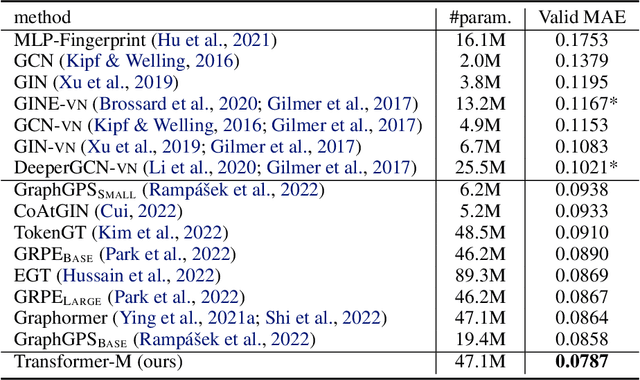
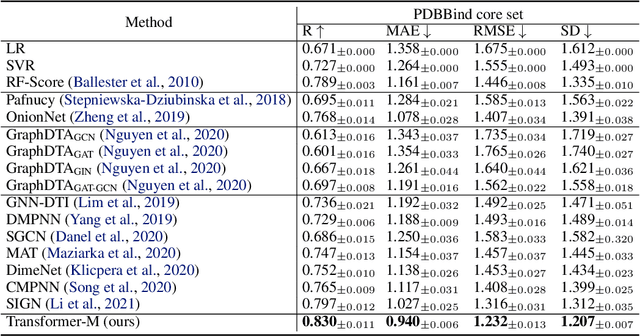
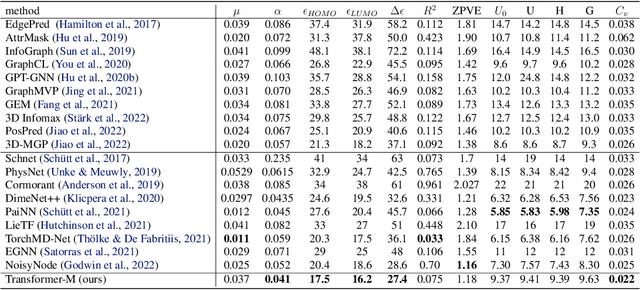
Abstract:Unlike vision and language data which usually has a unique format, molecules can naturally be characterized using different chemical formulations. One can view a molecule as a 2D graph or define it as a collection of atoms located in a 3D space. For molecular representation learning, most previous works designed neural networks only for a particular data format, making the learned models likely to fail for other data formats. We believe a general-purpose neural network model for chemistry should be able to handle molecular tasks across data modalities. To achieve this goal, in this work, we develop a novel Transformer-based Molecular model called Transformer-M, which can take molecular data of 2D or 3D formats as input and generate meaningful semantic representations. Using the standard Transformer as the backbone architecture, Transformer-M develops two separated channels to encode 2D and 3D structural information and incorporate them with the atom features in the network modules. When the input data is in a particular format, the corresponding channel will be activated, and the other will be disabled. By training on 2D and 3D molecular data with properly designed supervised signals, Transformer-M automatically learns to leverage knowledge from different data modalities and correctly capture the representations. We conducted extensive experiments for Transformer-M. All empirical results show that Transformer-M can simultaneously achieve strong performance on 2D and 3D tasks, suggesting its broad applicability. The code and models will be made publicly available at https://github.com/lsj2408/Transformer-M.
Rethinking Lipschitz Neural Networks for Certified L-infinity Robustness
Oct 04, 2022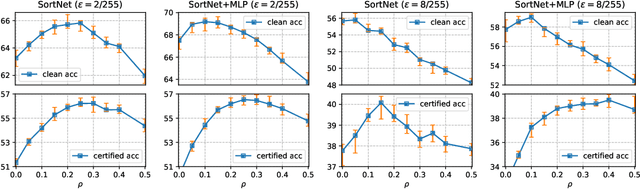
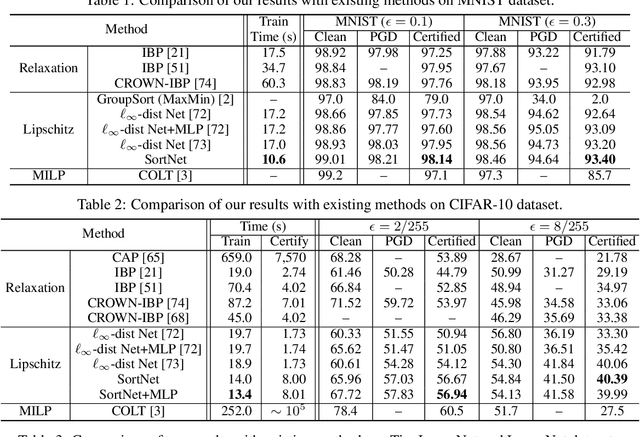
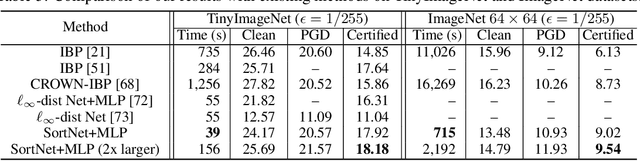
Abstract:Designing neural networks with bounded Lipschitz constant is a promising way to obtain certifiably robust classifiers against adversarial examples. However, the relevant progress for the important $\ell_\infty$ perturbation setting is rather limited, and a principled understanding of how to design expressive $\ell_\infty$ Lipschitz networks is still lacking. In this paper, we bridge the gap by studying certified $\ell_\infty$ robustness from a novel perspective of representing Boolean functions. We derive two fundamental impossibility results that hold for any standard Lipschitz network: one for robust classification on finite datasets, and the other for Lipschitz function approximation. These results identify that networks built upon norm-bounded affine layers and Lipschitz activations intrinsically lose expressive power even in the two-dimensional case, and shed light on how recently proposed Lipschitz networks (e.g., GroupSort and $\ell_\infty$-distance nets) bypass these impossibilities by leveraging order statistic functions. Finally, based on these insights, we develop a unified Lipschitz network that generalizes prior works, and design a practical version that can be efficiently trained (making certified robust training free). Extensive experiments show that our approach is scalable, efficient, and consistently yields better certified robustness across multiple datasets and perturbation radii than prior Lipschitz networks.
Check and Link: Pairwise Lesion Correspondence Guides Mammogram Mass Detection
Sep 13, 2022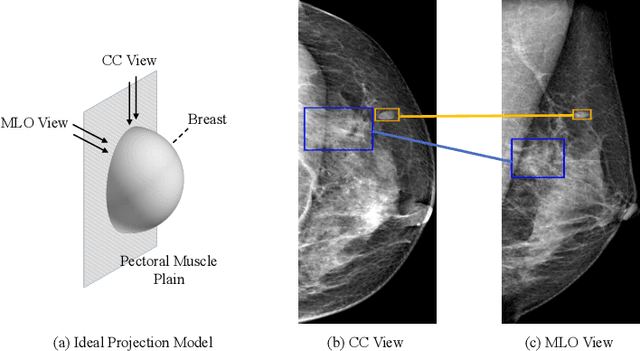
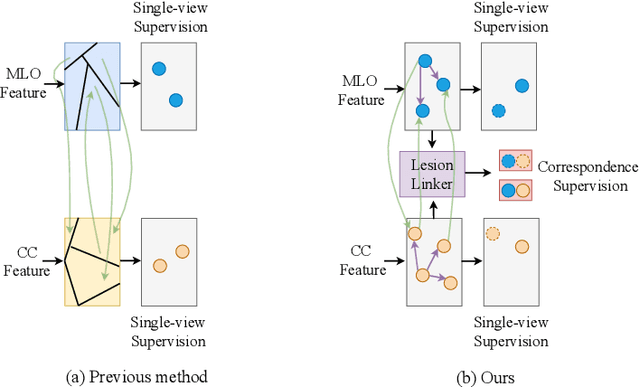
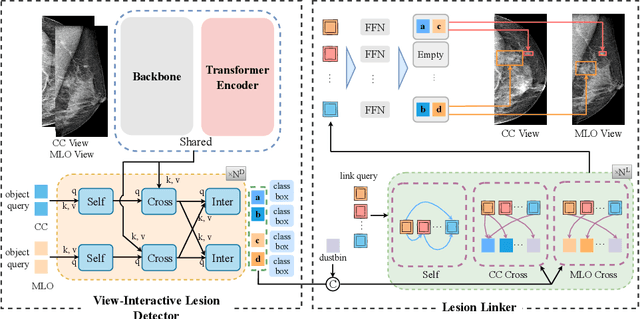
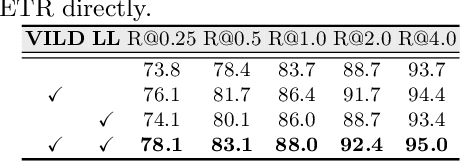
Abstract:Detecting mass in mammogram is significant due to the high occurrence and mortality of breast cancer. In mammogram mass detection, modeling pairwise lesion correspondence explicitly is particularly important. However, most of the existing methods build relatively coarse correspondence and have not utilized correspondence supervision. In this paper, we propose a new transformer-based framework CL-Net to learn lesion detection and pairwise correspondence in an end-to-end manner. In CL-Net, View-Interactive Lesion Detector is proposed to achieve dynamic interaction across candidates of cross views, while Lesion Linker employs the correspondence supervision to guide the interaction process more accurately. The combination of these two designs accomplishes precise understanding of pairwise lesion correspondence for mammograms. Experiments show that CL-Net yields state-of-the-art performance on the public DDSM dataset and our in-house dataset. Moreover, it outperforms previous methods by a large margin in low FPI regime.
PointScatter: Point Set Representation for Tubular Structure Extraction
Sep 13, 2022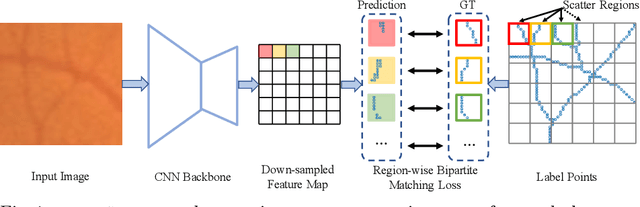
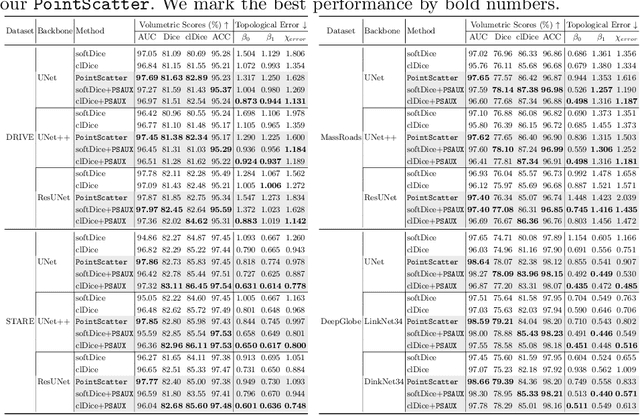
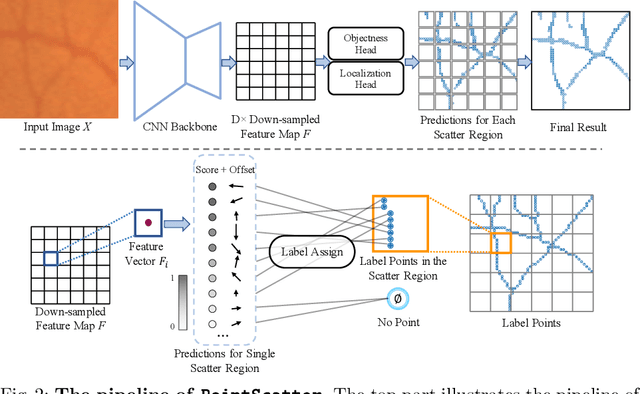
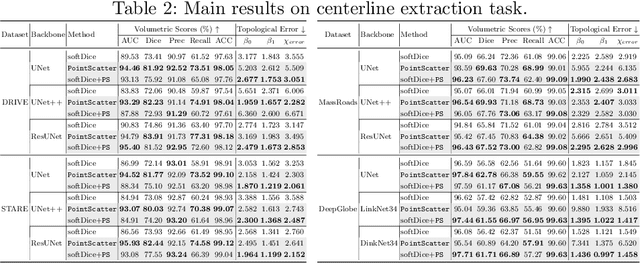
Abstract:This paper explores the point set representation for tubular structure extraction tasks. Compared with the traditional mask representation, the point set representation enjoys its flexibility and representation ability, which would not be restricted by the fixed grid as the mask. Inspired by this, we propose PointScatter, an alternative to the segmentation models for the tubular structure extraction task. PointScatter splits the image into scatter regions and parallelly predicts points for each scatter region. We further propose the greedy-based region-wise bipartite matching algorithm to train the network end-to-end and efficiently. We benchmark the PointScatter on four public tubular datasets, and the extensive experiments on tubular structure segmentation and centerline extraction task demonstrate the effectiveness of our approach. Code is available at https://github.com/zhangzhao2022/pointscatter.
Boosting 3D Object Detection via Object-Focused Image Fusion
Jul 21, 2022
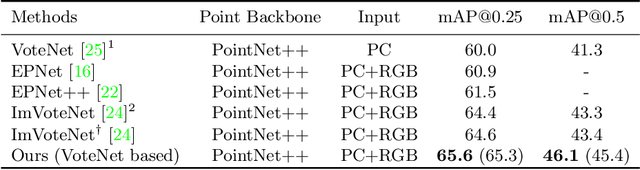

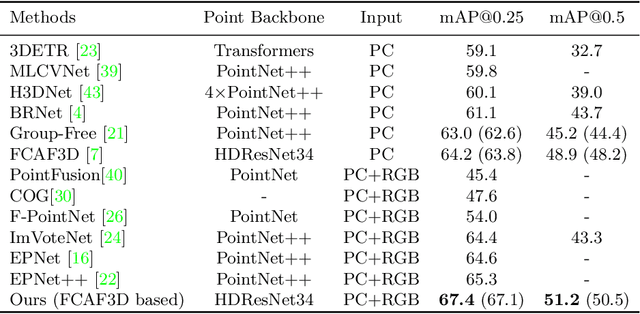
Abstract:3D object detection has achieved remarkable progress by taking point clouds as the only input. However, point clouds often suffer from incomplete geometric structures and the lack of semantic information, which makes detectors hard to accurately classify detected objects. In this work, we focus on how to effectively utilize object-level information from images to boost the performance of point-based 3D detector. We present DeMF, a simple yet effective method to fuse image information into point features. Given a set of point features and image feature maps, DeMF adaptively aggregates image features by taking the projected 2D location of the 3D point as reference. We evaluate our method on the challenging SUN RGB-D dataset, improving state-of-the-art results by a large margin (+2.1 mAP@0.25 and +2.3mAP@0.5). Code is available at https://github.com/haoy945/DeMF.
DecoupleNet: Decoupled Network for Domain Adaptive Semantic Segmentation
Jul 20, 2022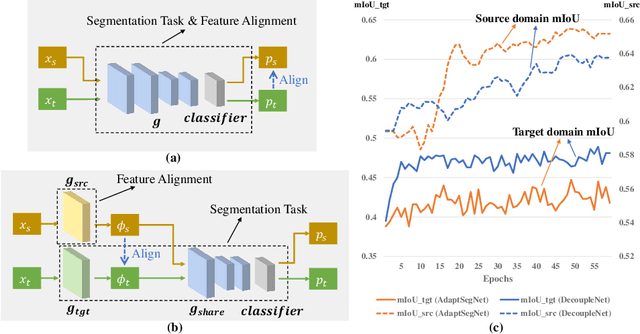
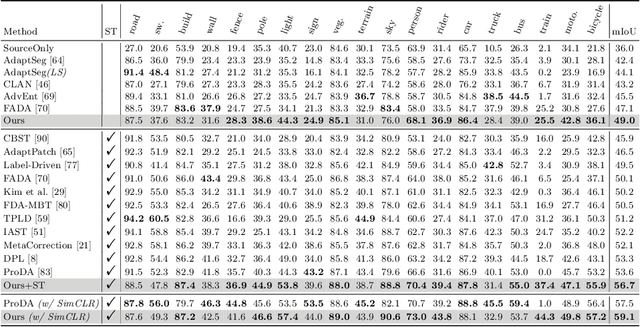
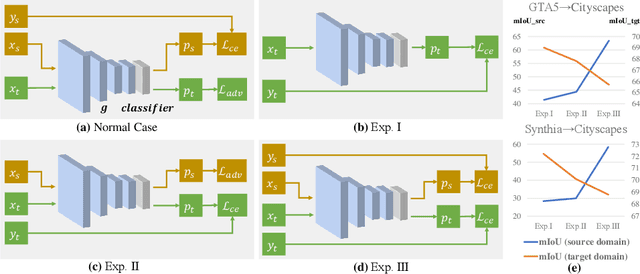
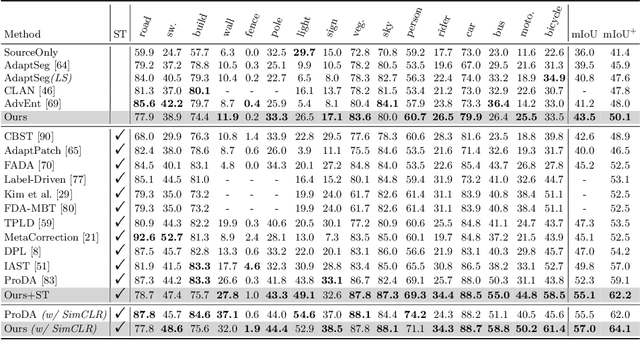
Abstract:Unsupervised domain adaptation in semantic segmentation has been raised to alleviate the reliance on expensive pixel-wise annotations. It leverages a labeled source domain dataset as well as unlabeled target domain images to learn a segmentation network. In this paper, we observe two main issues of the existing domain-invariant learning framework. (1) Being distracted by the feature distribution alignment, the network cannot focus on the segmentation task. (2) Fitting source domain data well would compromise the target domain performance. To address these issues, we propose DecoupleNet that alleviates source domain overfitting and enables the final model to focus more on the segmentation task. Furthermore, we put forward Self-Discrimination (SD) and introduce an auxiliary classifier to learn more discriminative target domain features with pseudo labels. Finally, we propose Online Enhanced Self-Training (OEST) to contextually enhance the quality of pseudo labels in an online manner. Experiments show our method outperforms existing state-of-the-art methods, and extensive ablation studies verify the effectiveness of each component. Code is available at https://github.com/dvlab-research/DecoupleNet.
Is $L^2$ Physics-Informed Loss Always Suitable for Training Physics-Informed Neural Network?
Jun 04, 2022
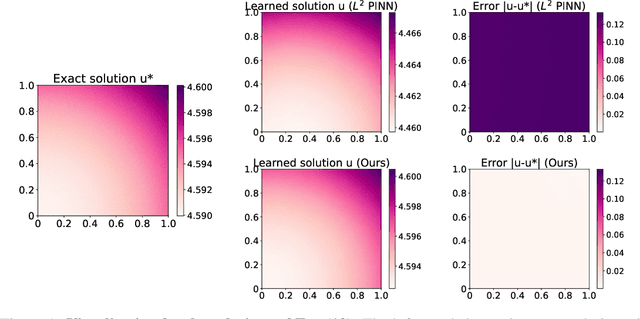
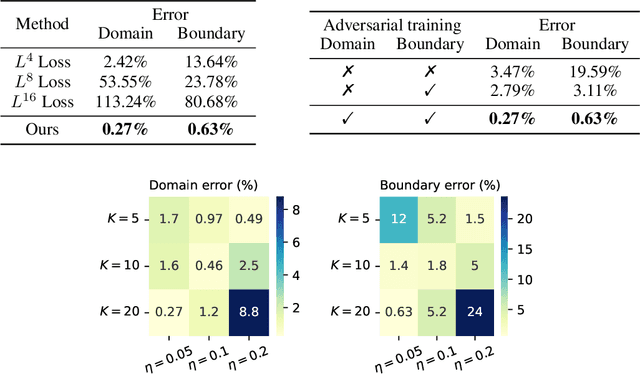
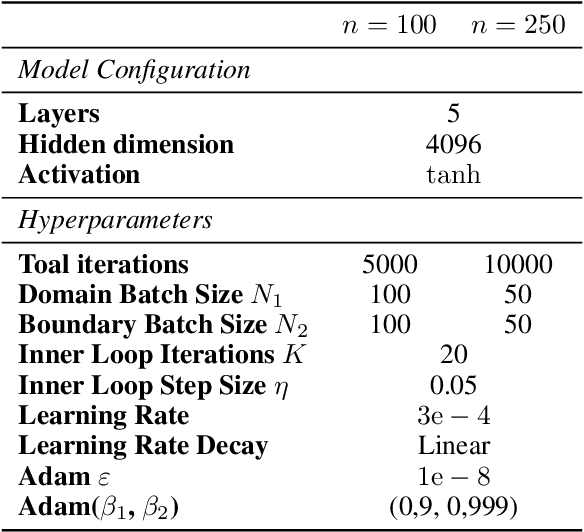
Abstract:The Physics-Informed Neural Network (PINN) approach is a new and promising way to solve partial differential equations using deep learning. The $L^2$ Physics-Informed Loss is the de-facto standard in training Physics-Informed Neural Networks. In this paper, we challenge this common practice by investigating the relationship between the loss function and the approximation quality of the learned solution. In particular, we leverage the concept of stability in the literature of partial differential equation to study the asymptotic behavior of the learned solution as the loss approaches zero. With this concept, we study an important class of high-dimensional non-linear PDEs in optimal control, the Hamilton-Jacobi-Bellman(HJB) Equation, and prove that for general $L^p$ Physics-Informed Loss, a wide class of HJB equation is stable only if $p$ is sufficiently large. Therefore, the commonly used $L^2$ loss is not suitable for training PINN on those equations, while $L^{\infty}$ loss is a better choice. Based on the theoretical insight, we develop a novel PINN training algorithm to minimize the $L^{\infty}$ loss for HJB equations which is in a similar spirit to adversarial training. The effectiveness of the proposed algorithm is empirically demonstrated through experiments.
Voxel Field Fusion for 3D Object Detection
May 31, 2022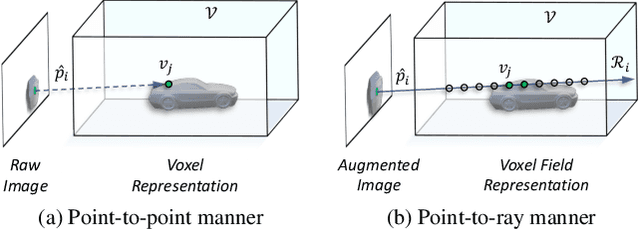

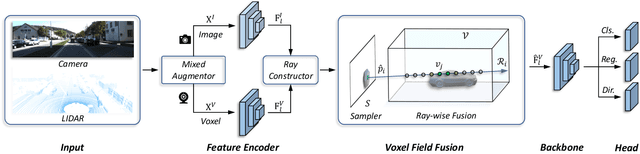
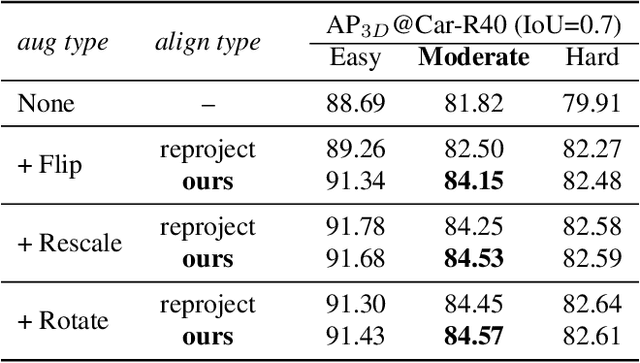
Abstract:In this work, we present a conceptually simple yet effective framework for cross-modality 3D object detection, named voxel field fusion. The proposed approach aims to maintain cross-modality consistency by representing and fusing augmented image features as a ray in the voxel field. To this end, the learnable sampler is first designed to sample vital features from the image plane that are projected to the voxel grid in a point-to-ray manner, which maintains the consistency in feature representation with spatial context. In addition, ray-wise fusion is conducted to fuse features with the supplemental context in the constructed voxel field. We further develop mixed augmentor to align feature-variant transformations, which bridges the modality gap in data augmentation. The proposed framework is demonstrated to achieve consistent gains in various benchmarks and outperforms previous fusion-based methods on KITTI and nuScenes datasets. Code is made available at https://github.com/dvlab-research/VFF.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge