Discovering Hierarchical Latent Capabilities of Language Models via Causal Representation Learning

Faithful evaluation of language model capabilities is crucial for deriving actionable insights that can inform model development. However, rigorous causal evaluations in this domain face significant methodological challenges, including complex confounding effects and prohibitive computational costs associated with extensive retraining. To tackle these challenges, we propose a causal representation learning framework wherein observed benchmark performance is modeled as a linear transformation of a few latent capability factors. Crucially, these latent factors are identified as causally interrelated after appropriately controlling for the base model as a common confounder. Applying this approach to a comprehensive dataset encompassing over 1500 models evaluated across six benchmarks from the Open LLM Leaderboard, we identify a concise three-node linear causal structure that reliably explains the observed performance variations. Further interpretation of this causal structure provides substantial scientific insights beyond simple numerical rankings: specifically, we reveal a clear causal direction starting from general problem-solving capabilities, advancing through instruction-following proficiency, and culminating in mathematical reasoning ability. Our results underscore the essential role of carefully controlling base model variations during evaluation, a step critical to accurately uncovering the underlying causal relationships among latent model capabilities.

Solving Inequality Proofs with Large Language Models

Inequality proving, crucial across diverse scientific and mathematical fields, tests advanced reasoning skills such as discovering tight bounds and strategic theorem application. This makes it a distinct, demanding frontier for large language models (LLMs), offering insights beyond general mathematical problem-solving. Progress in this area is hampered by existing datasets that are often scarce, synthetic, or rigidly formal. We address this by proposing an informal yet verifiable task formulation, recasting inequality proving into two automatically checkable subtasks: bound estimation and relation prediction. Building on this, we release IneqMath, an expert-curated dataset of Olympiad-level inequalities, including a test set and training corpus enriched with step-wise solutions and theorem annotations. We also develop a novel LLM-as-judge evaluation framework, combining a final-answer judge with four step-wise judges designed to detect common reasoning flaws. A systematic evaluation of 29 leading LLMs on IneqMath reveals a surprising reality: even top models like o1 achieve less than 10% overall accuracy under step-wise scrutiny; this is a drop of up to 65.5% from their accuracy considering only final answer equivalence. This discrepancy exposes fragile deductive chains and a critical gap for current LLMs between merely finding an answer and constructing a rigorous proof. Scaling model size and increasing test-time computation yield limited gains in overall proof correctness. Instead, our findings highlight promising research directions such as theorem-guided reasoning and self-refinement. Code and data are available at https://ineqmath.github.io/.

Structure-agnostic Optimality of Doubly Robust Learning for Treatment Effect Estimation

Average treatment effect estimation is the most central problem in causal inference with application to numerous disciplines. While many estimation strategies have been proposed in the literature, the statistical optimality of these methods has still remained an open area of investigation, especially in regimes where these methods do not achieve parametric rates. In this paper, we adopt the recently introduced structure-agnostic framework of statistical lower bounds, which poses no structural properties on the nuisance functions other than access to black-box estimators that achieve some statistical estimation rate. This framework is particularly appealing when one is only willing to consider estimation strategies that use non-parametric regression and classification oracles as black-box sub-processes. Within this framework, we prove the statistical optimality of the celebrated and widely used doubly robust estimators for both the Average Treatment Effect (ATE) and the Average Treatment Effect on the Treated (ATT), as well as weighted variants of the former, which arise in policy evaluation.

Dichotomy of Early and Late Phase Implicit Biases Can Provably Induce Grokking

Recent work by Power et al. (2022) highlighted a surprising "grokking" phenomenon in learning arithmetic tasks: a neural net first "memorizes" the training set, resulting in perfect training accuracy but near-random test accuracy, and after training for sufficiently longer, it suddenly transitions to perfect test accuracy. This paper studies the grokking phenomenon in theoretical setups and shows that it can be induced by a dichotomy of early and late phase implicit biases. Specifically, when training homogeneous neural nets with large initialization and small weight decay on both classification and regression tasks, we prove that the training process gets trapped at a solution corresponding to a kernel predictor for a long time, and then a very sharp transition to min-norm/max-margin predictors occurs, leading to a dramatic change in test accuracy.

Learning Causal Representations from General Environments: Identifiability and Intrinsic Ambiguity

This paper studies causal representation learning, the task of recovering high-level latent variables and their causal relationships from low-level data that we observe, assuming access to observations generated from multiple environments. While existing works are able to prove full identifiability of the underlying data generating process, they typically assume access to single-node, hard interventions which is rather unrealistic in practice. The main contribution of this paper is characterize a notion of identifiability which is provably the best one can achieve when hard interventions are not available. First, for linear causal models, we provide identifiability guarantee for data observed from general environments without assuming any similarities between them. While the causal graph is shown to be fully recovered, the latent variables are only identified up to an effect-domination ambiguity (EDA). We then propose an algorithm, LiNGCReL which is guaranteed to recover the ground-truth model up to EDA, and we demonstrate its effectiveness via numerical experiments. Moving on to general non-parametric causal models, we prove the same idenfifiability guarantee assuming access to groups of soft interventions. Finally, we provide counterparts of our identifiability results, indicating that EDA is basically inevitable in our setting.

Understanding Incremental Learning of Gradient Descent: A Fine-grained Analysis of Matrix Sensing

It is believed that Gradient Descent (GD) induces an implicit bias towards good generalization in training machine learning models. This paper provides a fine-grained analysis of the dynamics of GD for the matrix sensing problem, whose goal is to recover a low-rank ground-truth matrix from near-isotropic linear measurements. It is shown that GD with small initialization behaves similarly to the greedy low-rank learning heuristics (Li et al., 2020) and follows an incremental learning procedure (Gissin et al., 2019): GD sequentially learns solutions with increasing ranks until it recovers the ground truth matrix. Compared to existing works which only analyze the first learning phase for rank-1 solutions, our result provides characterizations for the whole learning process. Moreover, besides the over-parameterized regime that many prior works focused on, our analysis of the incremental learning procedure also applies to the under-parameterized regime. Finally, we conduct numerical experiments to confirm our theoretical findings.

Minimax Optimal Kernel Operator Learning via Multilevel Training

Learning mappings between infinite-dimensional function spaces has achieved empirical success in many disciplines of machine learning, including generative modeling, functional data analysis, causal inference, and multi-agent reinforcement learning. In this paper, we study the statistical limit of learning a Hilbert-Schmidt operator between two infinite-dimensional Sobolev reproducing kernel Hilbert spaces. We establish the information-theoretic lower bound in terms of the Sobolev Hilbert-Schmidt norm and show that a regularization that learns the spectral components below the bias contour and ignores the ones that are above the variance contour can achieve the optimal learning rate. At the same time, the spectral components between the bias and variance contours give us flexibility in designing computationally feasible machine learning algorithms. Based on this observation, we develop a multilevel kernel operator learning algorithm that is optimal when learning linear operators between infinite-dimensional function spaces.

Why Robust Generalization in Deep Learning is Difficult: Perspective of Expressive Power

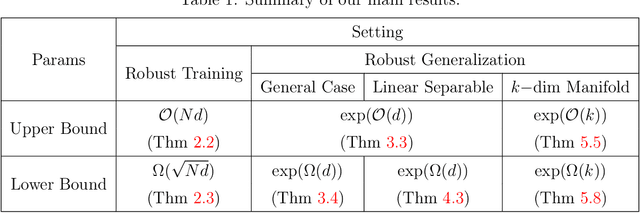
It is well-known that modern neural networks are vulnerable to adversarial examples. To mitigate this problem, a series of robust learning algorithms have been proposed. However, although the robust training error can be near zero via some methods, all existing algorithms lead to a high robust generalization error. In this paper, we provide a theoretical understanding of this puzzling phenomenon from the perspective of expressive power for deep neural networks. Specifically, for binary classification problems with well-separated data, we show that, for ReLU networks, while mild over-parameterization is sufficient for high robust training accuracy, there exists a constant robust generalization gap unless the size of the neural network is exponential in the data dimension $d$. Even if the data is linear separable, which means achieving low clean generalization error is easy, we can still prove an $\exp({\Omega}(d))$ lower bound for robust generalization. Moreover, we establish an improved upper bound of $\exp({\mathcal{O}}(k))$ for the network size to achieve low robust generalization error when the data lies on a manifold with intrinsic dimension $k$ ($k \ll d$). Nonetheless, we also have a lower bound that grows exponentially with respect to $k$ -- the curse of dimensionality is inevitable. By demonstrating an exponential separation between the network size for achieving low robust training and generalization error, our results reveal that the hardness of robust generalization may stem from the expressive power of practical models.

A Riemannian Accelerated Proximal Extragradient Framework and its Implications

The study of accelerated gradient methods in Riemannian optimization has recently witnessed notable progress. However, in contrast with the Euclidean setting, a systematic understanding of acceleration is still lacking in the Riemannian setting. We revisit the \emph{Accelerated Hybrid Proximal Extragradient} (A-HPE) method of \citet{monteiro2013accelerated}, a powerful framework for obtaining accelerated Euclidean methods. Subsequently, we propose a Riemannian version of A-HPE. The basis of our analysis of Riemannian A-HPE is a set of insights into Euclidean A-HPE, which we combine with a careful control of distortion caused by Riemannian geometry. We describe a number of Riemannian accelerated gradient methods as concrete instances of our framework.

Non-convex Distributionally Robust Optimization: Non-asymptotic Analysis

Distributionally robust optimization (DRO) is a widely-used approach to learn models that are robust against distribution shift. Compared with the standard optimization setting, the objective function in DRO is more difficult to optimize, and most of the existing theoretical results make strong assumptions on the loss function. In this work we bridge the gap by studying DRO algorithms for general smooth non-convex losses. By carefully exploiting the specific form of the DRO objective, we are able to provide non-asymptotic convergence guarantees even though the objective function is possibly non-convex, non-smooth and has unbounded gradient noise. In particular, we prove that a special algorithm called the mini-batch normalized gradient descent with momentum, can find an $\epsilon$ first-order stationary point within $O( \epsilon^{-4} )$ gradient complexity. We also discuss the conditional value-at-risk (CVaR) setting, where we propose a penalized DRO objective based on a smoothed version of the CVaR that allows us to obtain a similar convergence guarantee. We finally verify our theoretical results in a number of tasks and find that the proposed algorithm can consistently achieve prominent acceleration.