DMesh++: An Efficient Differentiable Mesh for Complex Shapes

Recent probabilistic methods for 3D triangular meshes capture diverse shapes by differentiable mesh connectivity, but face high computational costs with increased shape details. We introduce a new differentiable mesh processing method in 2D and 3D that addresses this challenge and efficiently handles meshes with intricate structures. Additionally, we present an algorithm that adapts the mesh resolution to local geometry in 2D for efficient representation. We demonstrate the effectiveness of our approach on 2D point cloud and 3D multi-view reconstruction tasks. Visit our project page (https://sonsang.github.io/dmesh2-project) for source code and supplementary material.

Differentiable Quantum Computing for Large-scale Linear Control

As industrial models and designs grow increasingly complex, the demand for optimal control of large-scale dynamical systems has significantly increased. However, traditional methods for optimal control incur significant overhead as problem dimensions grow. In this paper, we introduce an end-to-end quantum algorithm for linear-quadratic control with provable speedups. Our algorithm, based on a policy gradient method, incorporates a novel quantum subroutine for solving the matrix Lyapunov equation. Specifically, we build a quantum-assisted differentiable simulator for efficient gradient estimation that is more accurate and robust than classical methods relying on stochastic approximation. Compared to the classical approaches, our method achieves a super-quadratic speedup. To the best of our knowledge, this is the first end-to-end quantum application to linear control problems with provable quantum advantage.

Gradient Informed Proximal Policy Optimization

We introduce a novel policy learning method that integrates analytical gradients from differentiable environments with the Proximal Policy Optimization (PPO) algorithm. To incorporate analytical gradients into the PPO framework, we introduce the concept of an {\alpha}-policy that stands as a locally superior policy. By adaptively modifying the {\alpha} value, we can effectively manage the influence of analytical policy gradients during learning. To this end, we suggest metrics for assessing the variance and bias of analytical gradients, reducing dependence on these gradients when high variance or bias is detected. Our proposed approach outperforms baseline algorithms in various scenarios, such as function optimization, physics simulations, and traffic control environments. Our code can be found online: https://github.com/SonSang/gippo.

HandyPriors: Physically Consistent Perception of Hand-Object Interactions with Differentiable Priors

Various heuristic objectives for modeling hand-object interaction have been proposed in past work. However, due to the lack of a cohesive framework, these objectives often possess a narrow scope of applicability and are limited by their efficiency or accuracy. In this paper, we propose HandyPriors, a unified and general pipeline for pose estimation in human-object interaction scenes by leveraging recent advances in differentiable physics and rendering. Our approach employs rendering priors to align with input images and segmentation masks along with physics priors to mitigate penetration and relative-sliding across frames. Furthermore, we present two alternatives for hand and object pose estimation. The optimization-based pose estimation achieves higher accuracy, while the filtering-based tracking, which utilizes the differentiable priors as dynamics and observation models, executes faster. We demonstrate that HandyPriors attains comparable or superior results in the pose estimation task, and that the differentiable physics module can predict contact information for pose refinement. We also show that our approach generalizes to perception tasks, including robotic hand manipulation and human-object pose estimation in the wild.

Dynamic Mesh-Aware Radiance Fields

Embedding polygonal mesh assets within photorealistic Neural Radience Fields (NeRF) volumes, such that they can be rendered and their dynamics simulated in a physically consistent manner with the NeRF, is under-explored from the system perspective of integrating NeRF into the traditional graphics pipeline. This paper designs a two-way coupling between mesh and NeRF during rendering and simulation. We first review the light transport equations for both mesh and NeRF, then distill them into an efficient algorithm for updating radiance and throughput along a cast ray with an arbitrary number of bounces. To resolve the discrepancy between the linear color space that the path tracer assumes and the sRGB color space that standard NeRF uses, we train NeRF with High Dynamic Range (HDR) images. We also present a strategy to estimate light sources and cast shadows on the NeRF. Finally, we consider how the hybrid surface-volumetric formulation can be efficiently integrated with a high-performance physics simulator that supports cloth, rigid and soft bodies. The full rendering and simulation system can be run on a GPU at interactive rates. We show that a hybrid system approach outperforms alternatives in visual realism for mesh insertion, because it allows realistic light transport from volumetric NeRF media onto surfaces, which affects the appearance of reflective/refractive surfaces and illumination of diffuse surfaces informed by the dynamic scene.

Towards A Foundation Model for Generalist Robots: Diverse Skill Learning at Scale via Automated Task and Scene Generation

This document serves as a position paper that outlines the authors' vision for a potential pathway towards generalist robots. The purpose of this document is to share the excitement of the authors with the community and highlight a promising research direction in robotics and AI. The authors believe the proposed paradigm is a feasible path towards accomplishing the long-standing goal of robotics research: deploying robots, or embodied AI agents more broadly, in various non-factory real-world settings to perform diverse tasks. This document presents a specific idea for mining knowledge in the latest large-scale foundation models for robotics research. Instead of directly adapting these models or using them to guide low-level policy learning, it advocates for using them to generate diversified tasks and scenes at scale, thereby scaling up low-level skill learning and ultimately leading to a foundation model for robotics that empowers generalist robots. The authors are actively pursuing this direction, but in the meantime, they recognize that the ambitious goal of building generalist robots with large-scale policy training demands significant resources such as computing power and hardware, and research groups in academia alone may face severe resource constraints in implementing the entire vision. Therefore, the authors believe sharing their thoughts at this early stage could foster discussions, attract interest towards the proposed pathway and related topics from industry groups, and potentially spur significant technical advancements in the field.

PAC-NeRF: Physics Augmented Continuum Neural Radiance Fields for Geometry-Agnostic System Identification

Existing approaches to system identification (estimating the physical parameters of an object) from videos assume known object geometries. This precludes their applicability in a vast majority of scenes where object geometries are complex or unknown. In this work, we aim to identify parameters characterizing a physical system from a set of multi-view videos without any assumption on object geometry or topology. To this end, we propose "Physics Augmented Continuum Neural Radiance Fields" (PAC-NeRF), to estimate both the unknown geometry and physical parameters of highly dynamic objects from multi-view videos. We design PAC-NeRF to only ever produce physically plausible states by enforcing the neural radiance field to follow the conservation laws of continuum mechanics. For this, we design a hybrid Eulerian-Lagrangian representation of the neural radiance field, i.e., we use the Eulerian grid representation for NeRF density and color fields, while advecting the neural radiance fields via Lagrangian particles. This hybrid Eulerian-Lagrangian representation seamlessly blends efficient neural rendering with the material point method (MPM) for robust differentiable physics simulation. We validate the effectiveness of our proposed framework on geometry and physical parameter estimation over a vast range of materials, including elastic bodies, plasticine, sand, Newtonian and non-Newtonian fluids, and demonstrate significant performance gain on most tasks.

Differentiable Analog Quantum Computing for Optimization and Control

We formulate the first differentiable analog quantum computing framework with a specific parameterization design at the analog signal (pulse) level to better exploit near-term quantum devices via variational methods. We further propose a scalable approach to estimate the gradients of quantum dynamics using a forward pass with Monte Carlo sampling, which leads to a quantum stochastic gradient descent algorithm for scalable gradient-based training in our framework. Applying our framework to quantum optimization and control, we observe a significant advantage of differentiable analog quantum computing against SOTAs based on parameterized digital quantum circuits by orders of magnitude.

Differentiable Hybrid Traffic Simulation

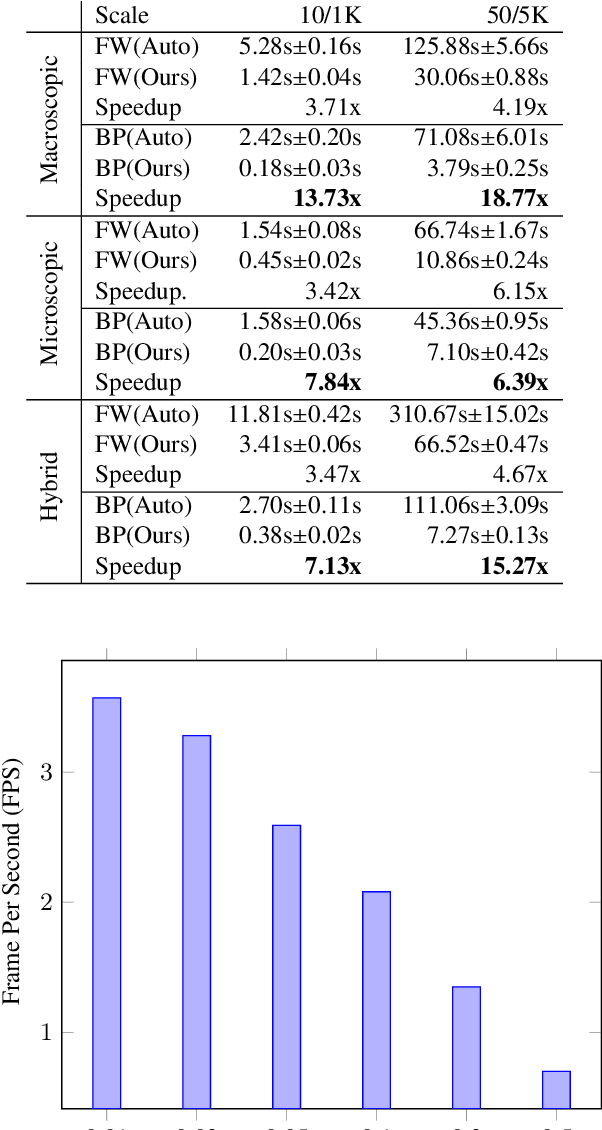
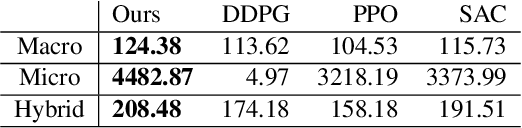
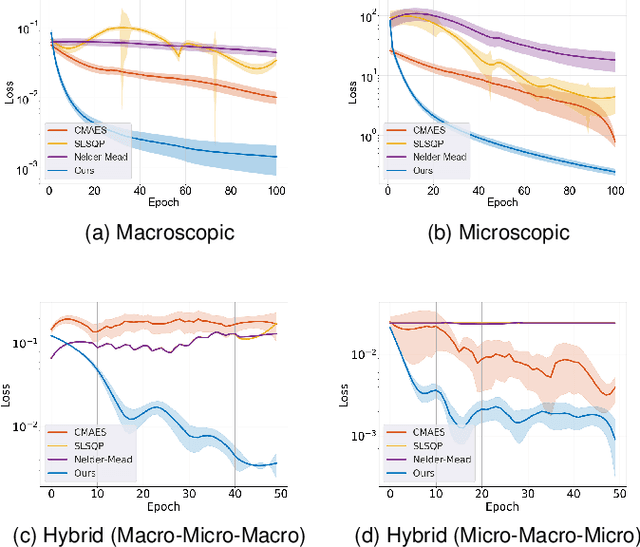
We introduce a novel differentiable hybrid traffic simulator, which simulates traffic using a hybrid model of both macroscopic and microscopic models and can be directly integrated into a neural network for traffic control and flow optimization. This is the first differentiable traffic simulator for macroscopic and hybrid models that can compute gradients for traffic states across time steps and inhomogeneous lanes. To compute the gradient flow between two types of traffic models in a hybrid framework, we present a novel intermediate conversion component that bridges the lanes in a differentiable manner as well. We also show that we can use analytical gradients to accelerate the overall process and enhance scalability. Thanks to these gradients, our simulator can provide more efficient and scalable solutions for complex learning and control problems posed in traffic engineering than other existing algorithms. Refer to https://sites.google.com/umd.edu/diff-hybrid-traffic-sim for our project.

Differentiable Simulation of Soft Multi-body Systems

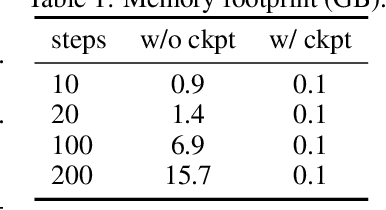
We present a method for differentiable simulation of soft articulated bodies. Our work enables the integration of differentiable physical dynamics into gradient-based pipelines. We develop a top-down matrix assembly algorithm within Projective Dynamics and derive a generalized dry friction model for soft continuum using a new matrix splitting strategy. We derive a differentiable control framework for soft articulated bodies driven by muscles, joint torques, or pneumatic tubes. The experiments demonstrate that our designs make soft body simulation more stable and realistic compared to other frameworks. Our method accelerates the solution of system identification problems by more than an order of magnitude, and enables efficient gradient-based learning of motion control with soft robots.