PCMind-2.1-Kaiyuan-2B Technical Report

The rapid advancement of Large Language Models (LLMs) has resulted in a significant knowledge gap between the open-source community and industry, primarily because the latter relies on closed-source, high-quality data and training recipes. To address this, we introduce PCMind-2.1-Kaiyuan-2B, a fully open-source 2-billion-parameter model focused on improving training efficiency and effectiveness under resource constraints. Our methodology includes three key innovations: a Quantile Data Benchmarking method for systematically comparing heterogeneous open-source datasets and providing insights on data mixing strategies; a Strategic Selective Repetition scheme within a multi-phase paradigm to effectively leverage sparse, high-quality data; and a Multi-Domain Curriculum Training policy that orders samples by quality. Supported by a highly optimized data preprocessing pipeline and architectural modifications for FP16 stability, Kaiyuan-2B achieves performance competitive with state-of-the-art fully open-source models, demonstrating practical and scalable solutions for resource-limited pretraining. We release all assets (including model weights, data, and code) under Apache 2.0 license at https://huggingface.co/thu-pacman/PCMind-2.1-Kaiyuan-2B.

Larger Datasets Can Be Repeated More: A Theoretical Analysis of Multi-Epoch Scaling in Linear Regression

While data scaling laws of large language models (LLMs) have been widely examined in the one-pass regime with massive corpora, their form under limited data and repeated epochs remains largely unexplored. This paper presents a theoretical analysis of how a common workaround, training for multiple epochs on the same dataset, reshapes the data scaling laws in linear regression. Concretely, we ask: to match the performance of training on a dataset of size $N$ for $K$ epochs, how much larger must a dataset be if the model is trained for only one pass? We quantify this using the \textit{effective reuse rate} of the data, $E(K, N)$, which we define as the multiplicative factor by which the dataset must grow under one-pass training to achieve the same test loss as $K$-epoch training. Our analysis precisely characterizes the scaling behavior of $E(K, N)$ for SGD in linear regression under either strong convexity or Zipf-distributed data: (1) When $K$ is small, we prove that $E(K, N) \approx K$, indicating that every new epoch yields a linear gain; (2) As $K$ increases, $E(K, N)$ plateaus at a problem-dependent value that grows with $N$ ($Θ(\log N)$ for the strongly-convex case), implying that larger datasets can be repeated more times before the marginal benefit vanishes. These theoretical findings point out a neglected factor in a recent empirical study (Muennighoff et al. (2023)), which claimed that training LLMs for up to $4$ epochs results in negligible loss differences compared to using fresh data at each step, \textit{i.e.}, $E(K, N) \approx K$ for $K \le 4$ in our notation. Supported by further empirical validation with LLMs, our results reveal that the maximum $K$ value for which $E(K, N) \approx K$ in fact depends on the data size and distribution, and underscore the need to explicitly model both factors in future studies of scaling laws with data reuse.

GLM-4.5: Agentic, Reasoning, and Coding (ARC) Foundation Models

We present GLM-4.5, an open-source Mixture-of-Experts (MoE) large language model with 355B total parameters and 32B activated parameters, featuring a hybrid reasoning method that supports both thinking and direct response modes. Through multi-stage training on 23T tokens and comprehensive post-training with expert model iteration and reinforcement learning, GLM-4.5 achieves strong performance across agentic, reasoning, and coding (ARC) tasks, scoring 70.1% on TAU-Bench, 91.0% on AIME 24, and 64.2% on SWE-bench Verified. With much fewer parameters than several competitors, GLM-4.5 ranks 3rd overall among all evaluated models and 2nd on agentic benchmarks. We release both GLM-4.5 (355B parameters) and a compact version, GLM-4.5-Air (106B parameters), to advance research in reasoning and agentic AI systems. Code, models, and more information are available at https://github.com/zai-org/GLM-4.5.

A Multi-Power Law for Loss Curve Prediction Across Learning Rate Schedules

Training large models is both resource-intensive and time-consuming, making it crucial to understand the quantitative relationship between model performance and hyperparameters. In this paper, we present an empirical law that describes how the pretraining loss of large language models evolves under different learning rate schedules, such as constant, cosine, and step decay schedules. Our proposed law takes a multi-power form, combining a power law based on the sum of learning rates and additional power laws to account for a loss reduction effect induced by learning rate decay. We extensively validate this law on various model sizes and architectures, and demonstrate that after fitting on a few learning rate schedules, the law accurately predicts the loss curves for unseen schedules of different shapes and horizons. Moreover, by minimizing the predicted final pretraining loss across learning rate schedules, we are able to find a schedule that outperforms the widely used cosine learning rate schedule. Interestingly, this automatically discovered schedule bears some resemblance to the recently proposed Warmup-Stable-Decay (WSD) schedule (Hu et al, 2024) but achieves a slightly lower final loss. We believe these results could offer valuable insights for understanding the dynamics of pretraining and designing learning rate schedules to improve efficiency.

Decoupling Knowledge and Reasoning in Transformers: A Modular Architecture with Generalized Cross-Attention

Transformers have achieved remarkable success across diverse domains, but their monolithic architecture presents challenges in interpretability, adaptability, and scalability. This paper introduces a novel modular Transformer architecture that explicitly decouples knowledge and reasoning through a generalized cross-attention mechanism to a globally shared knowledge base with layer-specific transformations, specifically designed for effective knowledge retrieval. Critically, we provide a rigorous mathematical derivation demonstrating that the Feed-Forward Network (FFN) in a standard Transformer is a specialized case (a closure) of this generalized cross-attention, revealing its role in implicit knowledge retrieval and validating our design. This theoretical framework provides a new lens for understanding FFNs and lays the foundation for future research exploring enhanced interpretability, adaptability, and scalability, enabling richer interplay with external knowledge bases and other systems.

Compression for Better: A General and Stable Lossless Compression Framework

This work focus on how to stabilize and lossless model compression, aiming to reduce model complexity and enhance efficiency without sacrificing performance due to compression errors. A key challenge is effectively leveraging compression errors and defining the boundaries for lossless compression to minimize model loss. i.e., compression for better. Currently, there is no systematic approach to determining this error boundary or understanding its specific impact on model performance. We propose a general \textbf{L}oss\textbf{L}ess \textbf{C}ompression theoretical framework (\textbf{LLC}), which further delineates the compression neighborhood and higher-order analysis boundaries through the total differential, thereby specifying the error range within which a model can be compressed without loss. To verify the effectiveness of LLC, we apply various compression techniques, including quantization and decomposition. Specifically, for quantization, we reformulate the classic quantization search problem as a grouped knapsack problem within the lossless neighborhood, achieving lossless quantization while improving computational efficiency. For decomposition, LLC addresses the approximation problem under low-rank constraints, automatically determining the rank for each layer and producing lossless low-rank models. We conduct extensive experiments on multiple neural network architectures on different datasets. The results show that without fancy tricks, LLC can effectively achieve lossless model compression. Our code will be made publicly.

A Comprehensive Survey on Distributed Training of Graph Neural Networks

Graph neural networks (GNNs) have been demonstrated to be a powerful algorithmic model in broad application fields for their effectiveness in learning over graphs. To scale GNN training up for large-scale and ever-growing graphs, the most promising solution is distributed training which distributes the workload of training across multiple computing nodes. However, the workflows, computational patterns, communication patterns, and optimization techniques of distributed GNN training remain preliminarily understood. In this paper, we provide a comprehensive survey of distributed GNN training by investigating various optimization techniques used in distributed GNN training. First, distributed GNN training is classified into several categories according to their workflows. In addition, their computational patterns and communication patterns, as well as the optimization techniques proposed by recent work are introduced. Second, the software frameworks and hardware platforms of distributed GNN training are also introduced for a deeper understanding. Third, distributed GNN training is compared with distributed training of deep neural networks, emphasizing the uniqueness of distributed GNN training. Finally, interesting issues and opportunities in this field are discussed.

GLM-130B: An Open Bilingual Pre-trained Model

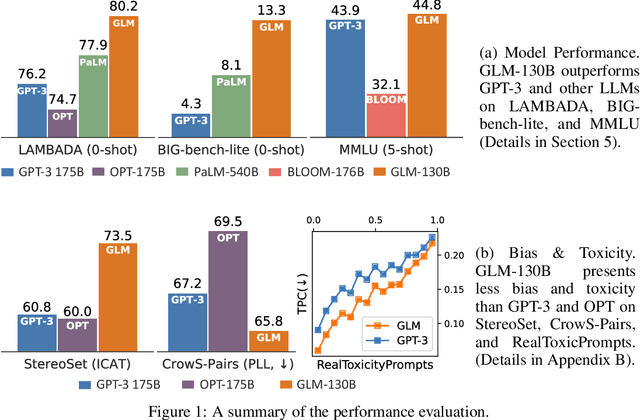
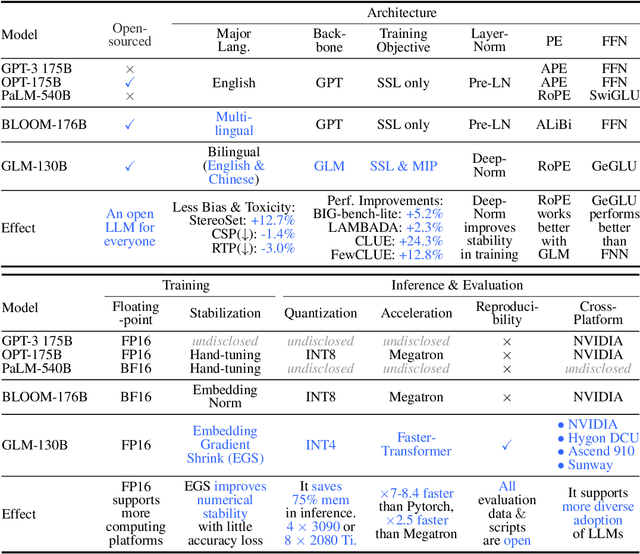
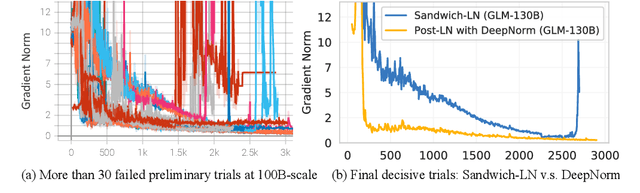
We introduce GLM-130B, a bilingual (English and Chinese) pre-trained language model with 130 billion parameters. It is an attempt to open-source a 100B-scale model at least as good as GPT-3 and unveil how models of such a scale can be successfully pre-trained. Over the course of this effort, we face numerous unexpected technical and engineering challenges, particularly on loss spikes and disconvergence. In this paper, we introduce the training process of GLM-130B including its design choices, training strategies for both efficiency and stability, and engineering efforts. The resultant GLM-130B model offers significant outperformance over GPT-3 175B on a wide range of popular English benchmarks while the performance advantage is not observed in OPT-175B and BLOOM-176B. It also consistently and significantly outperforms ERNIE TITAN 3.0 260B -- the largest Chinese language model -- across related benchmarks. Finally, we leverage a unique scaling property of GLM-130B to reach INT4 quantization, without quantization aware training and with almost no performance loss, making it the first among 100B-scale models. More importantly, the property allows its effective inference on 4$\times$RTX 3090 (24G) or 8$\times$RTX 2080 Ti (11G) GPUs, the most ever affordable GPUs required for using 100B-scale models. The GLM-130B model weights are publicly accessible and its code, training logs, related toolkit, and lessons learned are open-sourced at https://github.com/THUDM/GLM-130B .

Mixed-Precision Inference Quantization: Radically Towards Faster inference speed, Lower Storage requirement, and Lower Loss

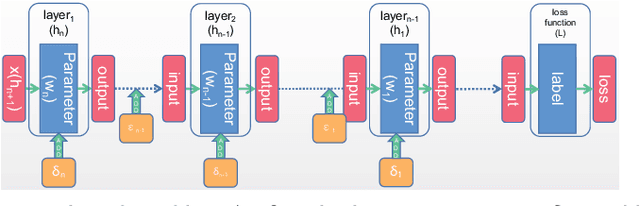
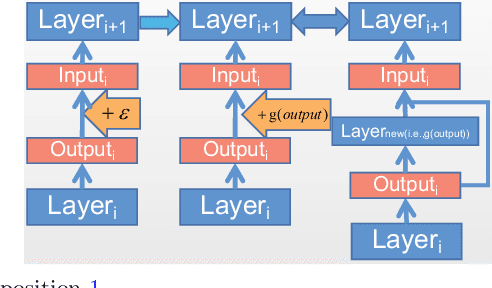
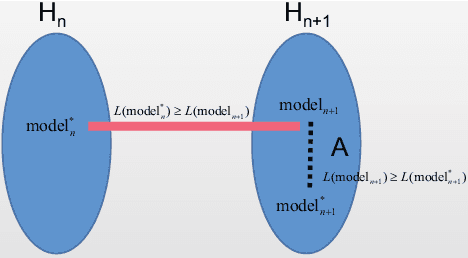
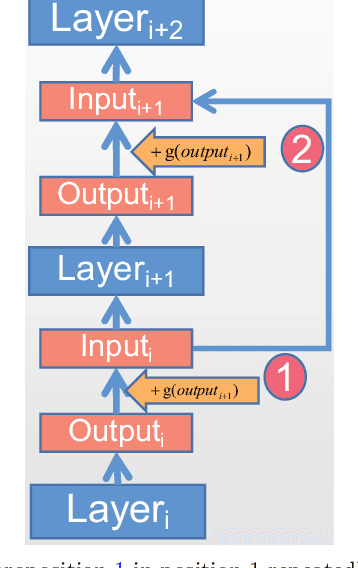
Based on the model's resilience to computational noise, model quantization is important for compressing models and improving computing speed. Existing quantization techniques rely heavily on experience and "fine-tuning" skills. In the majority of instances, the quantization model has a larger loss than a full precision model. This study provides a methodology for acquiring a mixed-precise quantization model with a lower loss than the full precision model. In addition, the analysis demonstrates that, throughout the inference process, the loss function is mostly affected by the noise of the layer inputs. In particular, we will demonstrate that neural networks with massive identity mappings are resistant to the quantization method. It is also difficult to improve the performance of these networks using quantization.

GraphTheta: A Distributed Graph Neural Network Learning System With Flexible Training Strategy

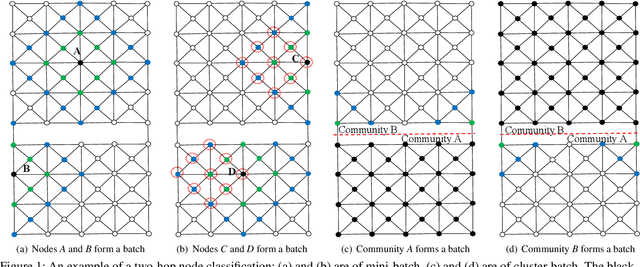
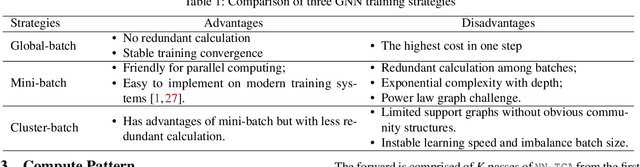
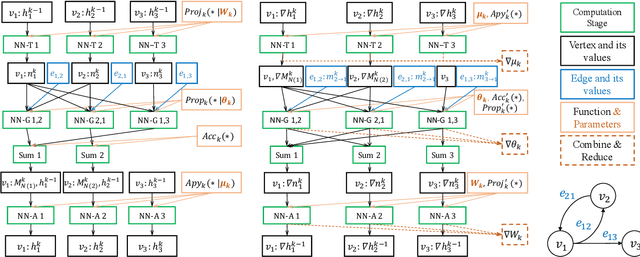
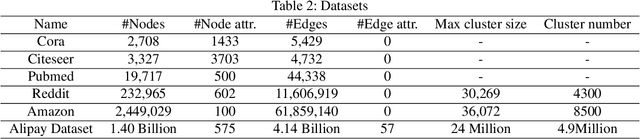
Graph neural networks (GNNs) have been demonstrated as a powerful tool for analysing non-Euclidean graph data. However, the lack of efficient distributed graph learning systems severely hinders applications of GNNs, especially when graphs are big, of high density or with highly skewed node degree distributions. In this paper, we present a new distributed graph learning system GraphTheta, which supports multiple training strategies and enables efficient and scalable learning on big graphs. GraphTheta implements both localized and globalized graph convolutions on graphs, where a new graph learning abstraction NN-TGAR is designed to bridge the gap between graph processing and graph learning frameworks. A distributed graph engine is proposed to conduct the stochastic gradient descent optimization with hybrid-parallel execution. Moreover, we add support for a new cluster-batched training strategy in addition to the conventional global-batched and mini-batched ones. We evaluate GraphTheta using a number of network data with network size ranging from small-, modest- to large-scale. Experimental results show that GraphTheta scales almost linearly to 1,024 workers and trains an in-house developed GNN model within 26 hours on Alipay dataset of 1.4 billion nodes and 4.1 billion attributed edges. Moreover, GraphTheta also obtains better prediction results than the state-of-the-art GNN methods. To the best of our knowledge, this work represents the largest edge-attributed GNN learning task conducted on a billion-scale network in the literature.