Larger Datasets Can Be Repeated More: A Theoretical Analysis of Multi-Epoch Scaling in Linear Regression

While data scaling laws of large language models (LLMs) have been widely examined in the one-pass regime with massive corpora, their form under limited data and repeated epochs remains largely unexplored. This paper presents a theoretical analysis of how a common workaround, training for multiple epochs on the same dataset, reshapes the data scaling laws in linear regression. Concretely, we ask: to match the performance of training on a dataset of size $N$ for $K$ epochs, how much larger must a dataset be if the model is trained for only one pass? We quantify this using the \textit{effective reuse rate} of the data, $E(K, N)$, which we define as the multiplicative factor by which the dataset must grow under one-pass training to achieve the same test loss as $K$-epoch training. Our analysis precisely characterizes the scaling behavior of $E(K, N)$ for SGD in linear regression under either strong convexity or Zipf-distributed data: (1) When $K$ is small, we prove that $E(K, N) \approx K$, indicating that every new epoch yields a linear gain; (2) As $K$ increases, $E(K, N)$ plateaus at a problem-dependent value that grows with $N$ ($Θ(\log N)$ for the strongly-convex case), implying that larger datasets can be repeated more times before the marginal benefit vanishes. These theoretical findings point out a neglected factor in a recent empirical study (Muennighoff et al. (2023)), which claimed that training LLMs for up to $4$ epochs results in negligible loss differences compared to using fresh data at each step, \textit{i.e.}, $E(K, N) \approx K$ for $K \le 4$ in our notation. Supported by further empirical validation with LLMs, our results reveal that the maximum $K$ value for which $E(K, N) \approx K$ in fact depends on the data size and distribution, and underscore the need to explicitly model both factors in future studies of scaling laws with data reuse.

A Multi-Power Law for Loss Curve Prediction Across Learning Rate Schedules

Training large models is both resource-intensive and time-consuming, making it crucial to understand the quantitative relationship between model performance and hyperparameters. In this paper, we present an empirical law that describes how the pretraining loss of large language models evolves under different learning rate schedules, such as constant, cosine, and step decay schedules. Our proposed law takes a multi-power form, combining a power law based on the sum of learning rates and additional power laws to account for a loss reduction effect induced by learning rate decay. We extensively validate this law on various model sizes and architectures, and demonstrate that after fitting on a few learning rate schedules, the law accurately predicts the loss curves for unseen schedules of different shapes and horizons. Moreover, by minimizing the predicted final pretraining loss across learning rate schedules, we are able to find a schedule that outperforms the widely used cosine learning rate schedule. Interestingly, this automatically discovered schedule bears some resemblance to the recently proposed Warmup-Stable-Decay (WSD) schedule (Hu et al, 2024) but achieves a slightly lower final loss. We believe these results could offer valuable insights for understanding the dynamics of pretraining and designing learning rate schedules to improve efficiency.

Exploring the Robustness of In-Context Learning with Noisy Labels

Recently, the mysterious In-Context Learning (ICL) ability exhibited by Transformer architectures, especially in large language models (LLMs), has sparked significant research interest. However, the resilience of Transformers' in-context learning capabilities in the presence of noisy samples, prevalent in both training corpora and prompt demonstrations, remains underexplored. In this paper, inspired by prior research that studies ICL ability using simple function classes, we take a closer look at this problem by investigating the robustness of Transformers against noisy labels. Specifically, we first conduct a thorough evaluation and analysis of the robustness of Transformers against noisy labels during in-context learning and show that they exhibit notable resilience against diverse types of noise in demonstration labels. Furthermore, we delve deeper into this problem by exploring whether introducing noise into the training set, akin to a form of data augmentation, enhances such robustness during inference, and find that such noise can indeed improve the robustness of ICL. Overall, our fruitful analysis and findings provide a comprehensive understanding of the resilience of Transformer models against label noises during ICL and provide valuable insights into the research on Transformers in natural language processing. Our code is available at https://github.com/InezYu0928/in-context-learning.

Rethinking the Graph Polynomial Filter via Positive and Negative Coupling Analysis

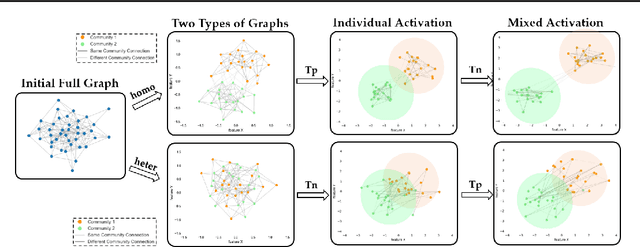
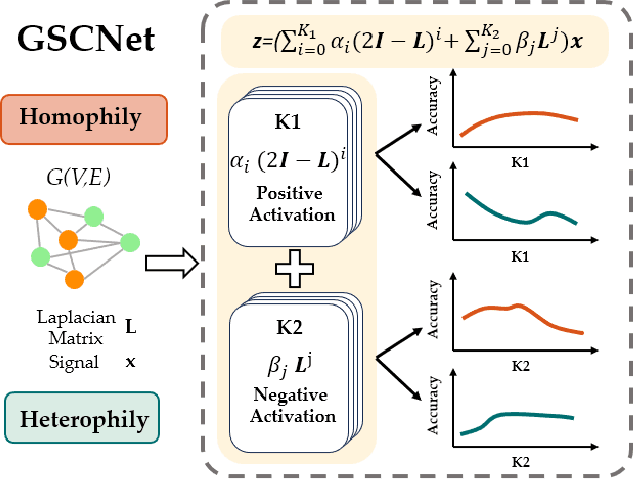
Recently, the optimization of polynomial filters within Spectral Graph Neural Networks (GNNs) has emerged as a prominent research focus. Existing spectral GNNs mainly emphasize polynomial properties in filter design, introducing computational overhead and neglecting the integration of crucial graph structure information. We argue that incorporating graph information into basis construction can enhance understanding of polynomial basis, and further facilitate simplified polynomial filter design. Motivated by this, we first propose a Positive and Negative Coupling Analysis (PNCA) framework, where the concepts of positive and negative activation are defined and their respective and mixed effects are analysed. Then, we explore PNCA from the message propagation perspective, revealing the subtle information hidden in the activation process. Subsequently, PNCA is used to analyze the mainstream polynomial filters, and a novel simple basis that decouples the positive and negative activation and fully utilizes graph structure information is designed. Finally, a simple GNN (called GSCNet) is proposed based on the new basis. Experimental results on the benchmark datasets for node classification verify that our GSCNet obtains better or comparable results compared with existing state-of-the-art GNNs while demanding relatively less computational time.