Deep Leaning-Based Ultra-Fast Stair Detection

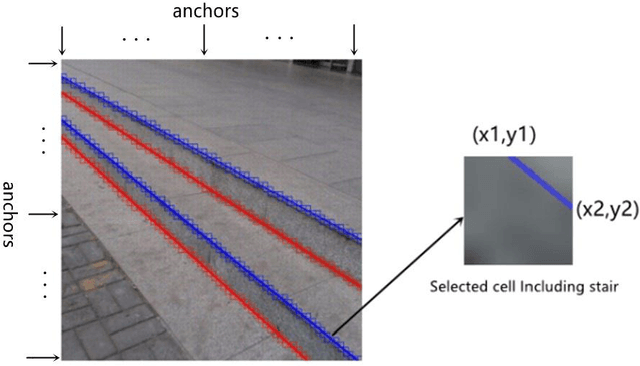
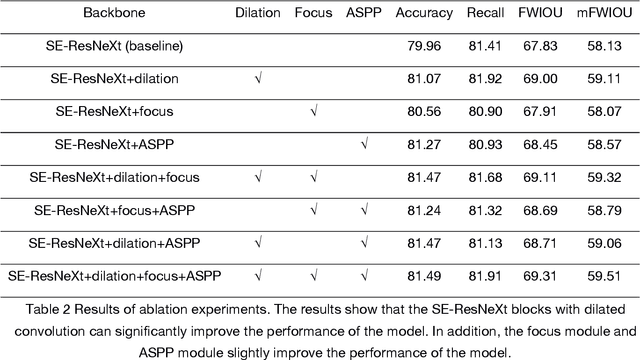
Staircases are some of the most common building structures in urban environments. Stair detection is an important task for various applications, including the environmental perception of exoskeleton robots, humanoid robots, and rescue robots and the navigation of visually impaired people. Most existing stair detection algorithms have difficulty dealing with the diversity of stair structure materials, extreme light and serious occlusion. Inspired by human perception, we propose an end-to-end method based on deep learning. Specifically, we treat the process of stair line detection as a multitask involving coarse-grained semantic segmentation and object detection. The input images are divided into cells, and a simple neural network is used to judge whether each cell contains stair lines. For cells containing stair lines, the locations of the stair lines relative to each cell are regressed. Extensive experiments on our dataset show that our method can achieve high performance in terms of both speed and accuracy. A lightweight version can even achieve 300+ frames per second with the same resolution. Our code and dataset will be soon available at GitHub.

Safe Screening for Sparse Conditional Random Fields

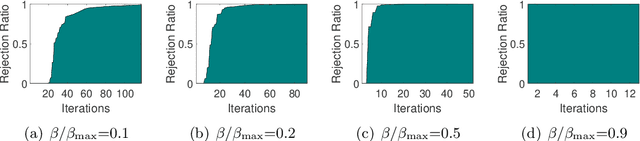
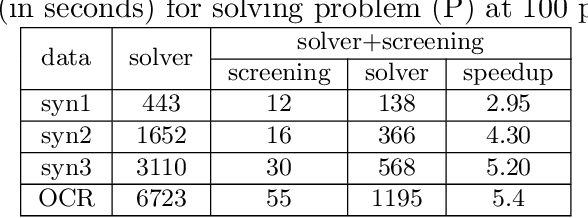
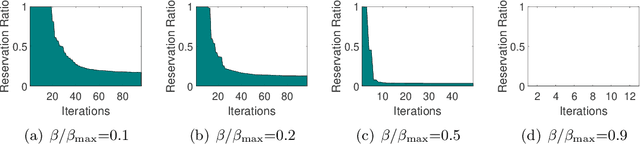
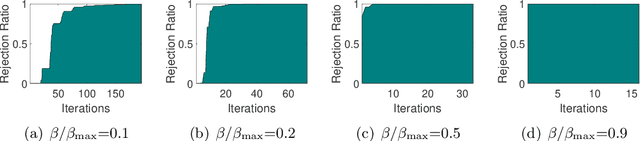
Sparse Conditional Random Field (CRF) is a powerful technique in computer vision and natural language processing for structured prediction. However, solving sparse CRFs in large-scale applications remains challenging. In this paper, we propose a novel safe dynamic screening method that exploits an accurate dual optimum estimation to identify and remove the irrelevant features during the training process. Thus, the problem size can be reduced continuously, leading to great savings in the computational cost without sacrificing any accuracy on the finally learned model. To the best of our knowledge, this is the first screening method which introduces the dual optimum estimation technique -- by carefully exploring and exploiting the strong convexity and the complex structure of the dual problem -- in static screening methods to dynamic screening. In this way, we can absorb the advantages of both the static and dynamic screening methods and avoid their drawbacks. Our estimation would be much more accurate than those developed based on the duality gap, which contributes to a much stronger screening rule. Moreover, our method is also the first screening method in sparse CRFs and even structure prediction models. Experimental results on both synthetic and real-world datasets demonstrate that the speedup gained by our method is significant.

On Reward-Free RL with Kernel and Neural Function Approximations: Single-Agent MDP and Markov Game

To achieve sample efficiency in reinforcement learning (RL), it necessitates efficiently exploring the underlying environment. Under the offline setting, addressing the exploration challenge lies in collecting an offline dataset with sufficient coverage. Motivated by such a challenge, we study the reward-free RL problem, where an agent aims to thoroughly explore the environment without any pre-specified reward function. Then, given any extrinsic reward, the agent computes the policy via a planning algorithm with offline data collected in the exploration phase. Moreover, we tackle this problem under the context of function approximation, leveraging powerful function approximators. Specifically, we propose to explore via an optimistic variant of the value-iteration algorithm incorporating kernel and neural function approximations, where we adopt the associated exploration bonus as the exploration reward. Moreover, we design exploration and planning algorithms for both single-agent MDPs and zero-sum Markov games and prove that our methods can achieve $\widetilde{\mathcal{O}}(1 /\varepsilon^2)$ sample complexity for generating a $\varepsilon$-suboptimal policy or $\varepsilon$-approximate Nash equilibrium when given an arbitrary extrinsic reward. To the best of our knowledge, we establish the first provably efficient reward-free RL algorithm with kernel and neural function approximators.

VisDrone-CC2020: The Vision Meets Drone Crowd Counting Challenge Results

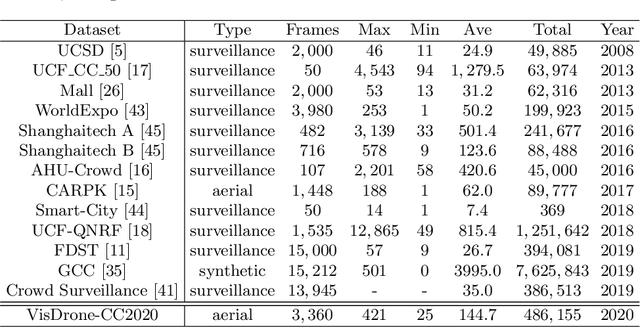
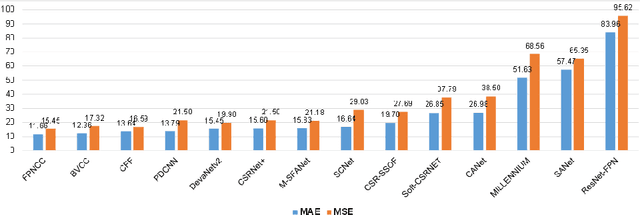
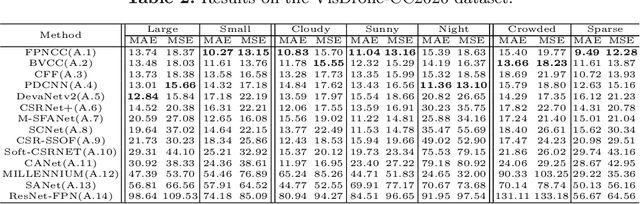
Crowd counting on the drone platform is an interesting topic in computer vision, which brings new challenges such as small object inference, background clutter and wide viewpoint. However, there are few algorithms focusing on crowd counting on the drone-captured data due to the lack of comprehensive datasets. To this end, we collect a large-scale dataset and organize the Vision Meets Drone Crowd Counting Challenge (VisDrone-CC2020) in conjunction with the 16th European Conference on Computer Vision (ECCV 2020) to promote the developments in the related fields. The collected dataset is formed by $3,360$ images, including $2,460$ images for training, and $900$ images for testing. Specifically, we manually annotate persons with points in each video frame. There are $14$ algorithms from $15$ institutes submitted to the VisDrone-CC2020 Challenge. We provide a detailed analysis of the evaluation results and conclude the challenge. More information can be found at the website: \url{http://www.aiskyeye.com/}.

Stylized Neural Painting

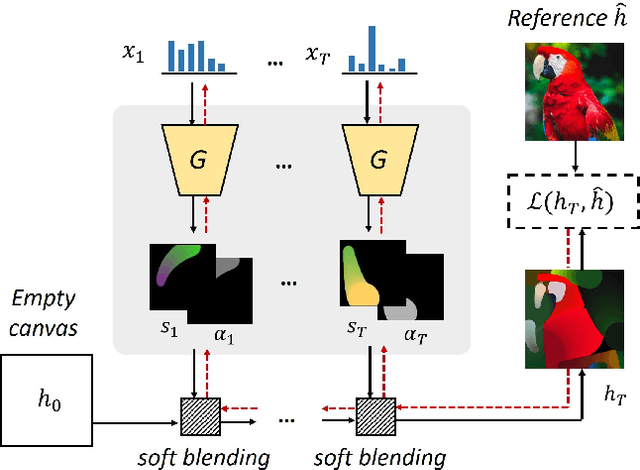
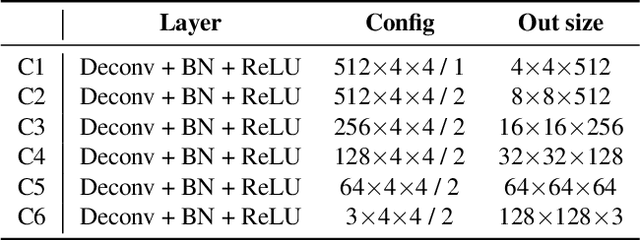
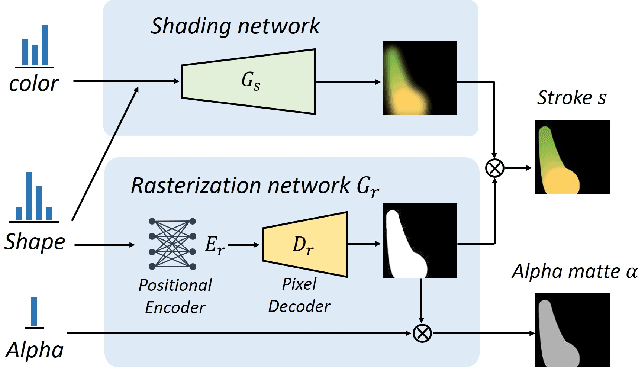
This paper proposes an image-to-painting translation method that generates vivid and realistic painting artworks with controllable styles. Different from previous image-to-image translation methods that formulate the translation as pixel-wise prediction, we deal with such an artistic creation process in a vectorized environment and produce a sequence of physically meaningful stroke parameters that can be further used for rendering. Since a typical vector render is not differentiable, we design a novel neural renderer which imitates the behavior of the vector renderer and then frame the stroke prediction as a parameter searching process that maximizes the similarity between the input and the rendering output. We explored the zero-gradient problem on parameter searching and propose to solve this problem from an optimal transportation perspective. We also show that previous neural renderers have a parameter coupling problem and we re-design the rendering network with a rasterization network and a shading network that better handles the disentanglement of shape and color. Experiments show that the paintings generated by our method have a high degree of fidelity in both global appearance and local textures. Our method can be also jointly optimized with neural style transfer that further transfers visual style from other images. Our code and animated results are available at \url{https://jiupinjia.github.io/neuralpainter/}.

Single-Timescale Stochastic Nonconvex-Concave Optimization for Smooth Nonlinear TD Learning

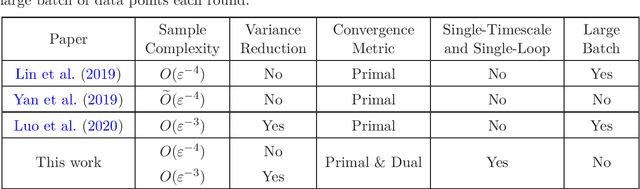
Temporal-Difference (TD) learning with nonlinear smooth function approximation for policy evaluation has achieved great success in modern reinforcement learning. It is shown that such a problem can be reformulated as a stochastic nonconvex-strongly-concave optimization problem, which is challenging as naive stochastic gradient descent-ascent algorithm suffers from slow convergence. Existing approaches for this problem are based on two-timescale or double-loop stochastic gradient algorithms, which may also require sampling large-batch data. However, in practice, a single-timescale single-loop stochastic algorithm is preferred due to its simplicity and also because its step-size is easier to tune. In this paper, we propose two single-timescale single-loop algorithms which require only one data point each step. Our first algorithm implements momentum updates on both primal and dual variables achieving an $O(\varepsilon^{-4})$ sample complexity, which shows the important role of momentum in obtaining a single-timescale algorithm. Our second algorithm improves upon the first one by applying variance reduction on top of momentum, which matches the best known $O(\varepsilon^{-3})$ sample complexity in existing works. Furthermore, our variance-reduction algorithm does not require a large-batch checkpoint. Moreover, our theoretical results for both algorithms are expressed in a tighter form of simultaneous primal and dual side convergence.

Beyond $\mathcal{O}(\sqrt{T})$ Regret for Constrained Online Optimization: Gradual Variations and Mirror Prox

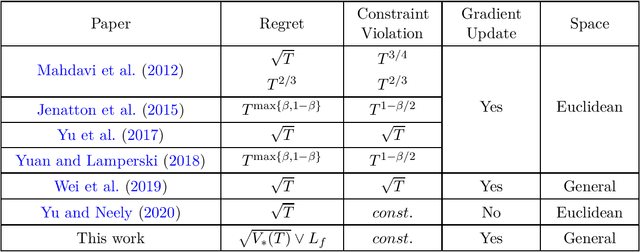
We study constrained online convex optimization, where the constraints consist of a relatively simple constraint set (e.g. a Euclidean ball) and multiple functional constraints. Projections onto such decision sets are usually computationally challenging. So instead of enforcing all constraints over each slot, we allow decisions to violate these functional constraints but aim at achieving a low regret and a low cumulative constraint violation over a horizon of $T$ time slot. The best known bound for solving this problem is $\mathcal{O}(\sqrt{T})$ regret and $\mathcal{O}(1)$ constraint violation, whose algorithms and analysis are restricted to Euclidean spaces. In this paper, we propose a new online primal-dual mirror prox algorithm whose regret is measured via a total gradient variation $V_*(T)$ over a sequence of $T$ loss functions. Specifically, we show that the proposed algorithm can achieve an $\mathcal{O}(\sqrt{V_*(T)})$ regret and $\mathcal{O}(1)$ constraint violation simultaneously. Such a bound holds in general non-Euclidean spaces, is never worse than the previously known $\big( \mathcal{O}(\sqrt{T}), \mathcal{O}(1) \big)$ result, and can be much better on regret when the variation is small. Furthermore, our algorithm is computationally efficient in that only two mirror descent steps are required during each slot instead of solving a general Lagrangian minimization problem. Along the way, our bounds also improve upon those of previous attempts using mirror-prox-type algorithms solving this problem, which yield a relatively worse $\mathcal{O}(T^{2/3})$ regret and $\mathcal{O}(T^{2/3})$ constraint violation.

Energy-Aware DNN Graph Optimization

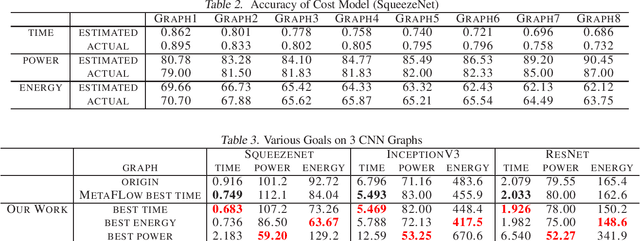
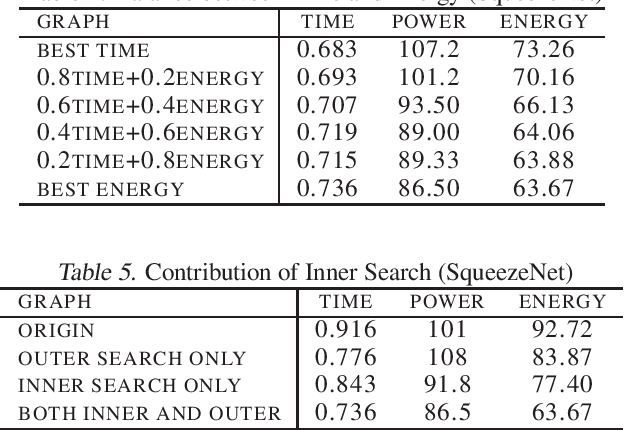
Unlike existing work in deep neural network (DNN) graphs optimization for inference performance, we explore DNN graph optimization for energy awareness and savings for power- and resource-constrained machine learning devices. We present a method that allows users to optimize energy consumption or balance between energy and inference performance for DNN graphs. This method efficiently searches through the space of equivalent graphs, and identifies a graph and the corresponding algorithms that incur the least cost in execution. We implement the method and evaluate it with multiple DNN models on a GPU-based machine. Results show that our method achieves significant energy savings, i.e., 24% with negligible performance impact.

Upper Confidence Primal-Dual Optimization: Stochastically Constrained Markov Decision Processes with Adversarial Losses and Unknown Transitions

We consider online learning for episodic Markov decision processes (MDPs) with stochastic long-term budget constraints, which plays a central role in ensuring the safety of reinforcement learning. Here the loss function can vary arbitrarily across the episodes, whereas both the loss received and the budget consumption are revealed at the end of each episode. Previous works solve this problem under the restrictive assumption that the transition model of the MDP is known a priori and establish regret bounds that depend polynomially on the cardinalities of the state space $\mathcal{S}$ and the action space $\mathcal{A}$. In this work, we propose a new \emph{upper confidence primal-dual} algorithm, which only requires the trajectories sampled from the transition model. In particular, we prove that the proposed algorithm achieves $\tilde{\mathcal{O}}(L|\mathcal{S}|\sqrt{|\mathcal{A}|T})$ upper bounds of both the regret and the constraint violation, where $L$ is the length of each episode. Our analysis incorporates a new high-probability drift analysis of Lagrange multiplier processes into the celebrated regret analysis of upper confidence reinforcement learning, which demonstrates the power of "optimism in the face of uncertainty" in constrained online learning.

Central Server Free Federated Learning over Single-sided Trust Social Networks

Federated learning has become increasingly important for modern machine learning, especially for data privacy-sensitive scenarios. Existing federated learning mostly adopts the central server-based architecture or centralized architecture. However, in many social network scenarios, centralized federated learning is not applicable (e.g., a central agent or server connecting all users may not exist, or the communication cost to the central server is not affordable). In this paper, we consider a generic setting: 1) the central server may not exist, and 2) the social network is unidirectional or of single-sided trust (i.e., user A trusts user B but user B may not trust user A). We propose a central server free federated learning algorithm, named Online Push-Sum (OPS) method, to handle this challenging but generic scenario. A rigorous regret analysis is also provided, which shows very interesting results on how users can benefit from communication with trusted users in the federated learning scenario. This work builds upon the fundamental algorithm framework and theoretical guarantees for federated learning in the generic social network scenario.