Beyond $\mathcal{O}(\sqrt{T})$ Regret for Constrained Online Optimization: Gradual Variations and Mirror Prox

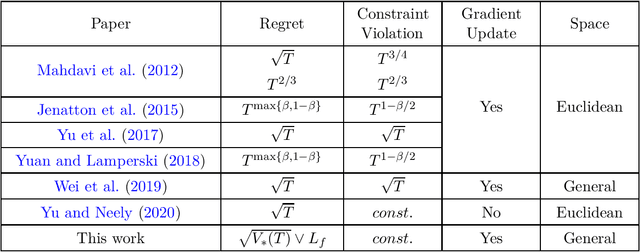
We study constrained online convex optimization, where the constraints consist of a relatively simple constraint set (e.g. a Euclidean ball) and multiple functional constraints. Projections onto such decision sets are usually computationally challenging. So instead of enforcing all constraints over each slot, we allow decisions to violate these functional constraints but aim at achieving a low regret and a low cumulative constraint violation over a horizon of $T$ time slot. The best known bound for solving this problem is $\mathcal{O}(\sqrt{T})$ regret and $\mathcal{O}(1)$ constraint violation, whose algorithms and analysis are restricted to Euclidean spaces. In this paper, we propose a new online primal-dual mirror prox algorithm whose regret is measured via a total gradient variation $V_*(T)$ over a sequence of $T$ loss functions. Specifically, we show that the proposed algorithm can achieve an $\mathcal{O}(\sqrt{V_*(T)})$ regret and $\mathcal{O}(1)$ constraint violation simultaneously. Such a bound holds in general non-Euclidean spaces, is never worse than the previously known $\big( \mathcal{O}(\sqrt{T}), \mathcal{O}(1) \big)$ result, and can be much better on regret when the variation is small. Furthermore, our algorithm is computationally efficient in that only two mirror descent steps are required during each slot instead of solving a general Lagrangian minimization problem. Along the way, our bounds also improve upon those of previous attempts using mirror-prox-type algorithms solving this problem, which yield a relatively worse $\mathcal{O}(T^{2/3})$ regret and $\mathcal{O}(T^{2/3})$ constraint violation.