RazorAttention: Efficient KV Cache Compression Through Retrieval Heads

The memory and computational demands of Key-Value (KV) cache present significant challenges for deploying long-context language models. Previous approaches attempt to mitigate this issue by selectively dropping tokens, which irreversibly erases critical information that might be needed for future queries. In this paper, we propose a novel compression technique for KV cache that preserves all token information. Our investigation reveals that: i) Most attention heads primarily focus on the local context; ii) Only a few heads, denoted as retrieval heads, can essentially pay attention to all input tokens. These key observations motivate us to use separate caching strategy for attention heads. Therefore, we propose RazorAttention, a training-free KV cache compression algorithm, which maintains a full cache for these crucial retrieval heads and discards the remote tokens in non-retrieval heads. Furthermore, we introduce a novel mechanism involving a "compensation token" to further recover the information in the dropped tokens. Extensive evaluations across a diverse set of large language models (LLMs) demonstrate that RazorAttention achieves a reduction in KV cache size by over 70% without noticeable impacts on performance. Additionally, RazorAttention is compatible with FlashAttention, rendering it an efficient and plug-and-play solution that enhances LLM inference efficiency without overhead or retraining of the original model.

EasyQuant: An Efficient Data-free Quantization Algorithm for LLMs

Large language models (LLMs) have proven to be very superior to conventional methods in various tasks. However, their expensive computations and high memory requirements are prohibitive for deployment. Model quantization is an effective method for reducing this overhead. The problem is that in most previous works, the quantized model was calibrated using few samples from the training data, which might affect the generalization of the quantized LLMs to unknown cases and tasks. Hence in this work, we explore an important question: Can we design a data-independent quantization method for LLMs to guarantee its generalization performance? In this work, we propose EasyQuant, a training-free and data-independent weight-only quantization algorithm for LLMs. Our observation indicates that two factors: outliers in the weight and quantization ranges, are essential for reducing the quantization error. Therefore, in EasyQuant, we leave the outliers (less than 1%) unchanged and optimize the quantization range to reduce the reconstruction error. With these methods, we surprisingly find that EasyQuant achieves comparable performance to the original model. Since EasyQuant does not depend on any training data, the generalization performance of quantized LLMs is safely guaranteed. Moreover, EasyQuant can be implemented in parallel so that the quantized model could be attained in a few minutes even for LLMs over 100B. To our best knowledge, we are the first work that achieves almost lossless quantization performance for LLMs under a data-independent setting and our algorithm runs over 10 times faster than the data-dependent methods.

MKQ-BERT: Quantized BERT with 4-bits Weights and Activations

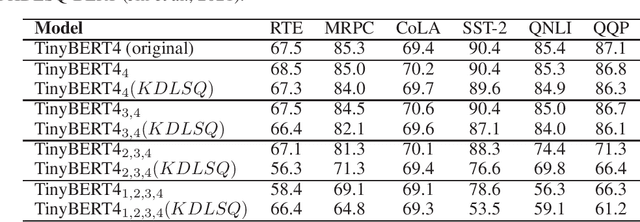
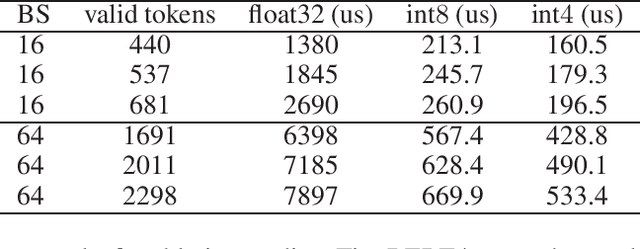
Recently, pre-trained Transformer based language models, such as BERT, have shown great superiority over the traditional methods in many Natural Language Processing (NLP) tasks. However, the computational cost for deploying these models is prohibitive on resource-restricted devices. One method to alleviate this computation overhead is to quantize the original model into fewer bits representation, and previous work has proved that we can at most quantize both weights and activations of BERT into 8-bits, without degrading its performance. In this work, we propose MKQ-BERT, which further improves the compression level and uses 4-bits for quantization. In MKQ-BERT, we propose a novel way for computing the gradient of the quantization scale, combined with an advanced distillation strategy. On the one hand, we prove that MKQ-BERT outperforms the existing BERT quantization methods for achieving a higher accuracy under the same compression level. On the other hand, we are the first work that successfully deploys the 4-bits BERT and achieves an end-to-end speedup for inference. Our results suggest that we could achieve 5.3x of bits reduction without degrading the model accuracy, and the inference speed of one int4 layer is 15x faster than a float32 layer in Transformer based model.

PASTO: Strategic Parameter Optimization in Recommendation Systems -- Probabilistic is Better than Deterministic

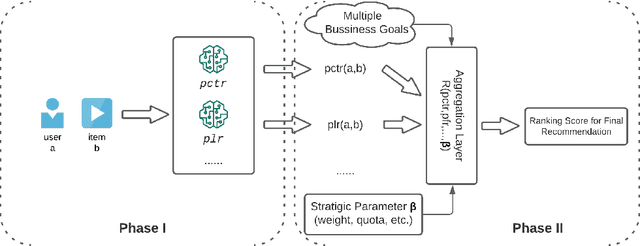
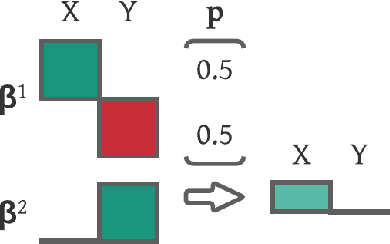
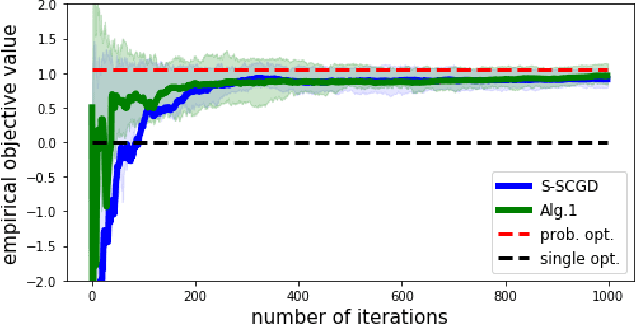
Real-world recommendation systems often consist of two phases. In the first phase, multiple predictive models produce the probability of different immediate user actions. In the second phase, these predictions are aggregated according to a set of 'strategic parameters' to meet a diverse set of business goals, such as longer user engagement, higher revenue potential, or more community/network interactions. In addition to building accurate predictive models, it is also crucial to optimize this set of 'strategic parameters' so that primary goals are optimized while secondary guardrails are not hurt. In this setting with multiple and constrained goals, this paper discovers that a probabilistic strategic parameter regime can achieve better value compared to the standard regime of finding a single deterministic parameter. The new probabilistic regime is to learn the best distribution over strategic parameter choices and sample one strategic parameter from the distribution when each user visits the platform. To pursue the optimal probabilistic solution, we formulate the problem into a stochastic compositional optimization problem, in which the unbiased stochastic gradient is unavailable. Our approach is applied in a popular social network platform with hundreds of millions of daily users and achieves +0.22% lift of user engagement in a recommendation task and +1.7% lift in revenue in an advertising optimization scenario comparing to using the best deterministic parameter strategy.

On the geometry of generalization and memorization in deep neural networks

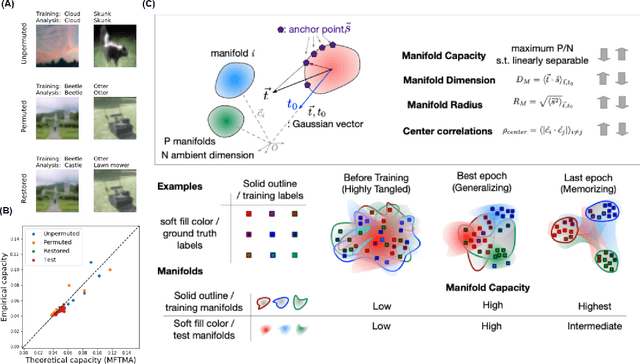
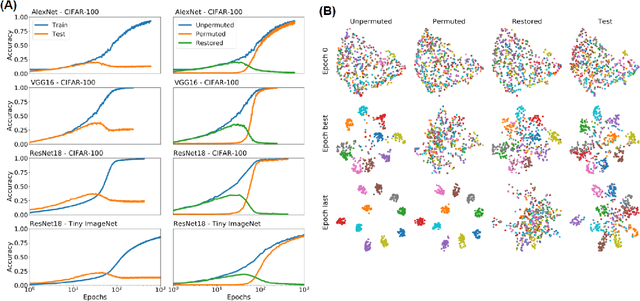
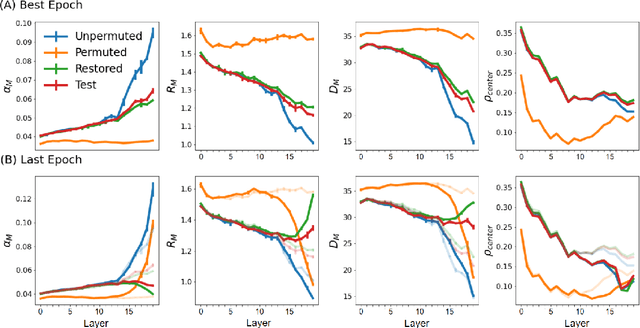
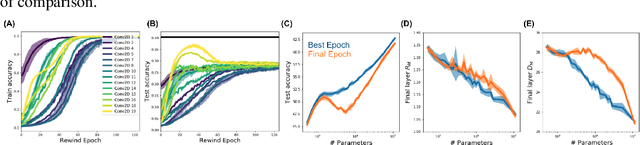
Understanding how large neural networks avoid memorizing training data is key to explaining their high generalization performance. To examine the structure of when and where memorization occurs in a deep network, we use a recently developed replica-based mean field theoretic geometric analysis method. We find that all layers preferentially learn from examples which share features, and link this behavior to generalization performance. Memorization predominately occurs in the deeper layers, due to decreasing object manifolds' radius and dimension, whereas early layers are minimally affected. This predicts that generalization can be restored by reverting the final few layer weights to earlier epochs before significant memorization occurred, which is confirmed by the experiments. Additionally, by studying generalization under different model sizes, we reveal the connection between the double descent phenomenon and the underlying model geometry. Finally, analytical analysis shows that networks avoid memorization early in training because close to initialization, the gradient contribution from permuted examples are small. These findings provide quantitative evidence for the structure of memorization across layers of a deep neural network, the drivers for such structure, and its connection to manifold geometric properties.

Syntactic Perturbations Reveal Representational Correlates of Hierarchical Phrase Structure in Pretrained Language Models

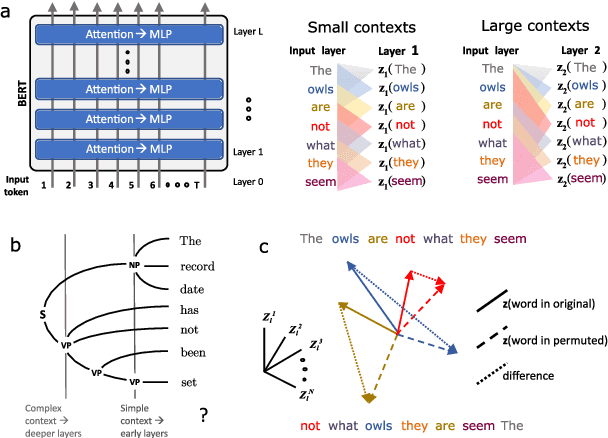
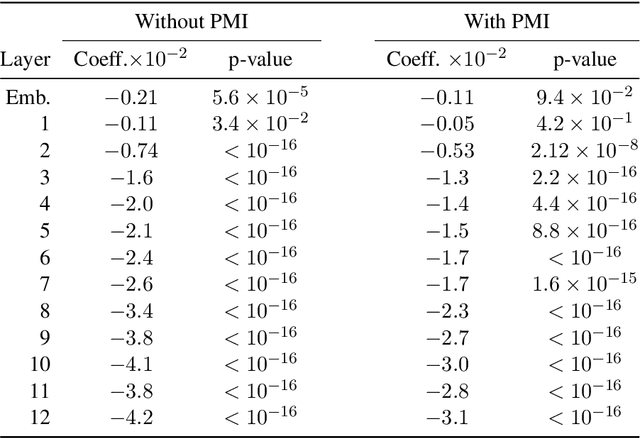
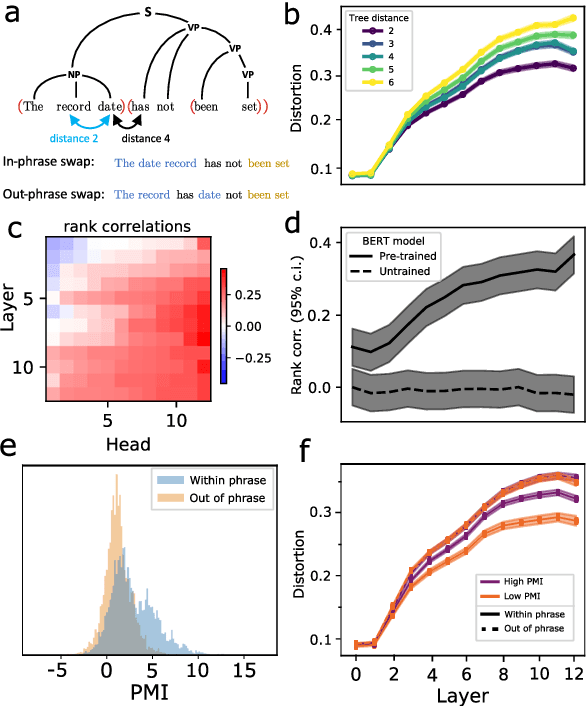
While vector-based language representations from pretrained language models have set a new standard for many NLP tasks, there is not yet a complete accounting of their inner workings. In particular, it is not entirely clear what aspects of sentence-level syntax are captured by these representations, nor how (if at all) they are built along the stacked layers of the network. In this paper, we aim to address such questions with a general class of interventional, input perturbation-based analyses of representations from pretrained language models. Importing from computational and cognitive neuroscience the notion of representational invariance, we perform a series of probes designed to test the sensitivity of these representations to several kinds of structure in sentences. Each probe involves swapping words in a sentence and comparing the representations from perturbed sentences against the original. We experiment with three different perturbations: (1) random permutations of n-grams of varying width, to test the scale at which a representation is sensitive to word position; (2) swapping of two spans which do or do not form a syntactic phrase, to test sensitivity to global phrase structure; and (3) swapping of two adjacent words which do or do not break apart a syntactic phrase, to test sensitivity to local phrase structure. Results from these probes collectively suggest that Transformers build sensitivity to larger parts of the sentence along their layers, and that hierarchical phrase structure plays a role in this process. More broadly, our results also indicate that structured input perturbations widens the scope of analyses that can be performed on often-opaque deep learning systems, and can serve as a complement to existing tools (such as supervised linear probes) for interpreting complex black-box models.

1-bit LAMB: Communication Efficient Large-Scale Large-Batch Training with LAMB's Convergence Speed

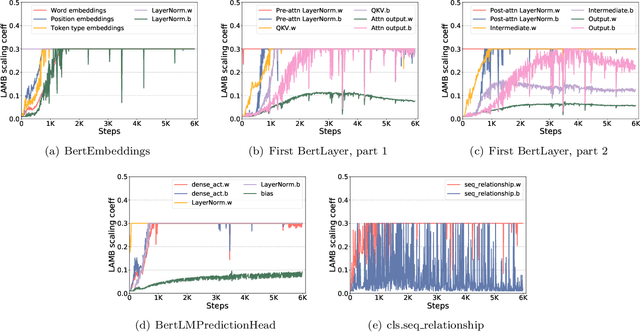
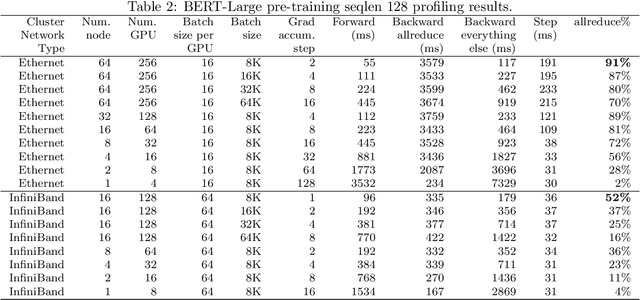
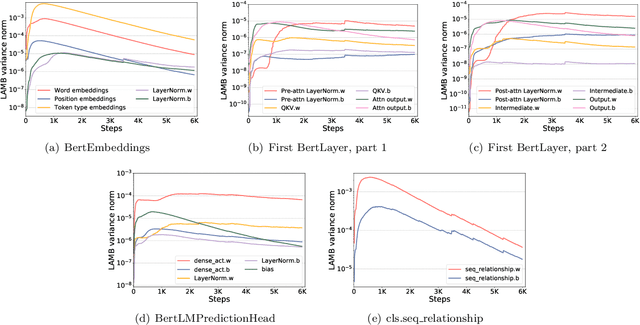
To train large models (like BERT and GPT-3) with hundreds or even thousands of GPUs, the communication has become a major bottleneck, especially on commodity systems with limited-bandwidth TCP interconnects network. On one side large-batch optimization such as LAMB algorithm was proposed to reduce the number of communications. On the other side, communication compression algorithms such as 1-bit SGD and 1-bit Adam help to reduce the volume of each communication. However, we find that simply using one of the techniques is not sufficient to solve the communication challenge, especially on low-bandwidth Ethernet networks. Motivated by this we aim to combine the power of large-batch optimization and communication compression, but we find that existing compression strategies cannot be directly applied to LAMB due to its unique adaptive layerwise learning rates. To this end, we design a new communication-efficient algorithm, 1-bit LAMB, which introduces a novel way to support adaptive layerwise learning rates even when communication is compressed. In addition, we introduce a new system implementation for compressed communication using the NCCL backend of PyTorch distributed, which improves both usability and performance compared to existing MPI-based implementation. For BERT-Large pre-training task with batch sizes from 8K to 64K, our evaluations on up to 256 GPUs demonstrate that 1-bit LAMB with NCCL-based backend is able to achieve up to 4.6x communication volume reduction, up to 2.8x end-to-end speedup (in terms of number of training samples per second), and the same convergence speed (in terms of number of pre-training samples to reach the same accuracy on fine-tuning tasks) compared to uncompressed LAMB.

1-bit Adam: Communication Efficient Large-Scale Training with Adam's Convergence Speed

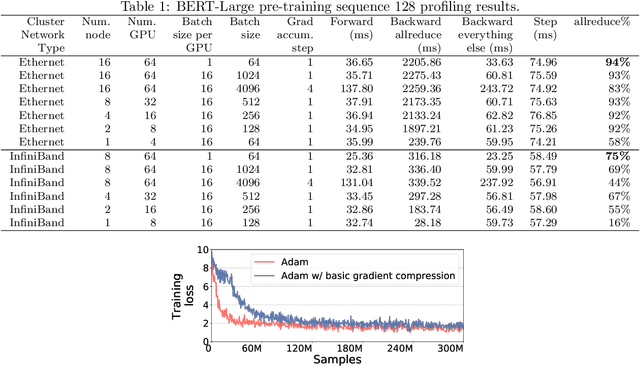
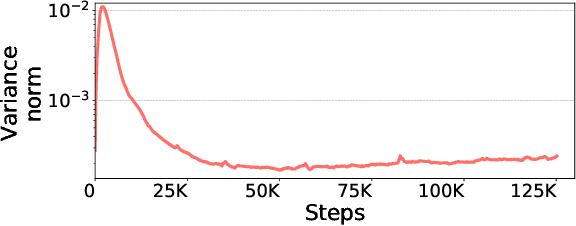
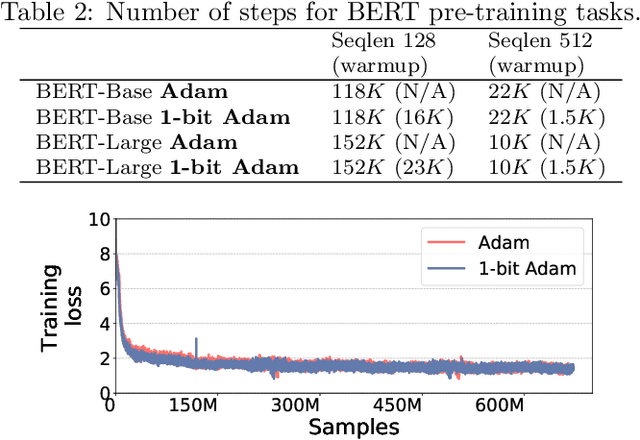
Scalable training of large models (like BERT and GPT-3) requires careful optimization rooted in model design, architecture, and system capabilities. From a system standpoint, communication has become a major bottleneck, especially on commodity systems with standard TCP interconnects that offer limited network bandwidth. Communication compression is an important technique to reduce training time on such systems. One of the most effective methods is error-compensated compression, which offers robust convergence speed even under 1-bit compression. However, state-of-the-art error compensation techniques only work with basic optimizers like SGD and momentum SGD, which are linearly dependent on the gradients. They do not work with non-linear gradient-based optimizers like Adam, which offer state-of-the-art convergence efficiency and accuracy for models like BERT. In this paper, we propose 1-bit Adam that reduces the communication volume by up to $5\times$, offers much better scalability, and provides the same convergence speed as uncompressed Adam. Our key finding is that Adam's variance (non-linear term) becomes stable (after a warmup phase) and can be used as a fixed precondition for the rest of the training (compression phase). Experiments on up to 256 GPUs show that 1-bit Adam enables up to $3.3\times$ higher throughput for BERT-Large pre-training and up to $2.9\times$ higher throughput for SQuAD fine-tuning. In addition, we provide theoretical analysis for our proposed work.

APMSqueeze: A Communication Efficient Adam-Preconditioned Momentum SGD Algorithm

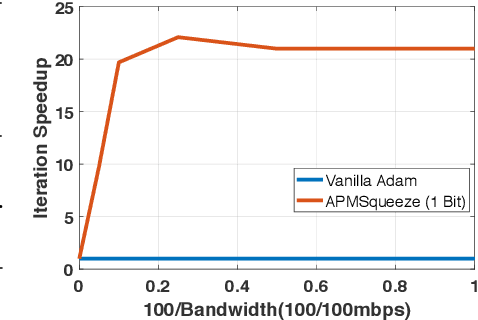
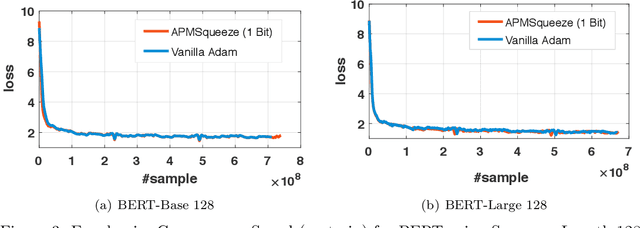
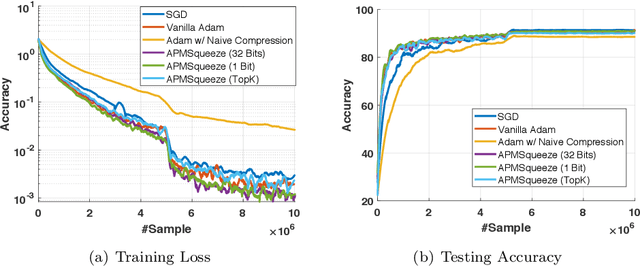
Adam is the important optimization algorithm to guarantee efficiency and accuracy for training many important tasks such as BERT and ImageNet. However, Adam is generally not compatible with information (gradient) compression technology. Therefore, the communication usually becomes the bottleneck for parallelizing Adam. In this paper, we propose a communication efficient {\bf A}DAM {\bf p}reconditioned {\bf M}omentum SGD algorithm-- named APMSqueeze-- through an error compensated method compressing gradients. The proposed algorithm achieves a similar convergence efficiency to Adam in term of epochs, but significantly reduces the running time per epoch. In terms of end-to-end performance (including the full-precision pre-condition step), APMSqueeze is able to provide {sometimes by up to $2-10\times$ speed-up depending on network bandwidth.} We also conduct theoretical analysis on the convergence and efficiency.

Optimizing Memory Placement using Evolutionary Graph Reinforcement Learning

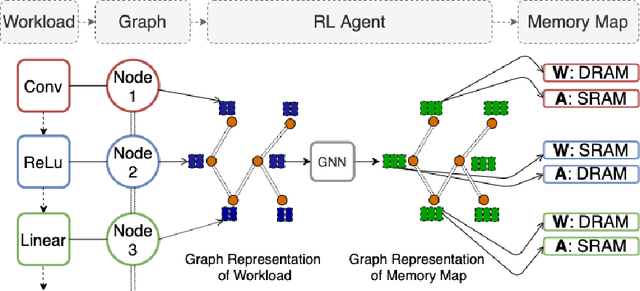
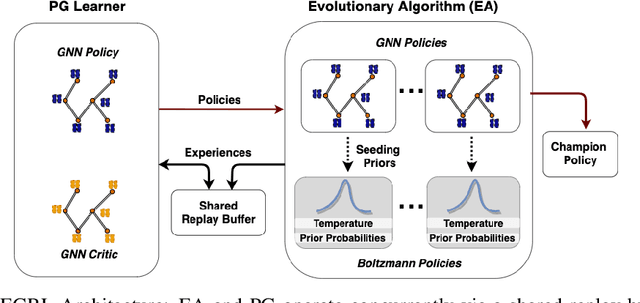
As modern neural networks have grown to billions of parameters, meeting tight latency budgets has become increasingly challenging. Approaches like compression, sparsification and network pruning have proven effective to tackle this problem - but they rely on modifications of the underlying network. In this paper, we look at a complimentary approach of optimizing how tensors are mapped to on-chip memory in an inference accelerator while leaving the network parameters untouched. Since different memory components trade off capacity for bandwidth differently, a sub-optimal mapping can result in high latency. We introduce evolutionary graph reinforcement learning (EGRL) - a method combining graph neural networks, reinforcement learning (RL) and evolutionary search - that aims to find the optimal mapping to minimize latency. Furthermore, a set of fast, stateless policies guide the evolutionary search to improve sample-efficiency. We train and validate our approach directly on the Intel NNP-I chip for inference using a batch size of 1. EGRL outperforms policy-gradient, evolutionary search and dynamic programming baselines on BERT, ResNet-101 and ResNet-50. We achieve 28-78% speed-up compared to the native NNP-I compiler on all three workloads.